
全程设计 3.1.2 国数的单调性 第3课时 函数的平均变化率
3.1.2 函数的单调性 第3课时 函数的平均变化率

课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.了解直线的斜率和函数的平均变化率的概念 2.理解函数的单调性与函数的平均变化率的关系. 3.能用函数的平均变化率证明函数的单调性
导航 课标定位素养阐释 1.了解直线的斜率和函数的平均变化率的概念. 2.理解函数的单调性与函数的平均变化率的关系. 3.能用函数的平均变化率证明函数的单调性
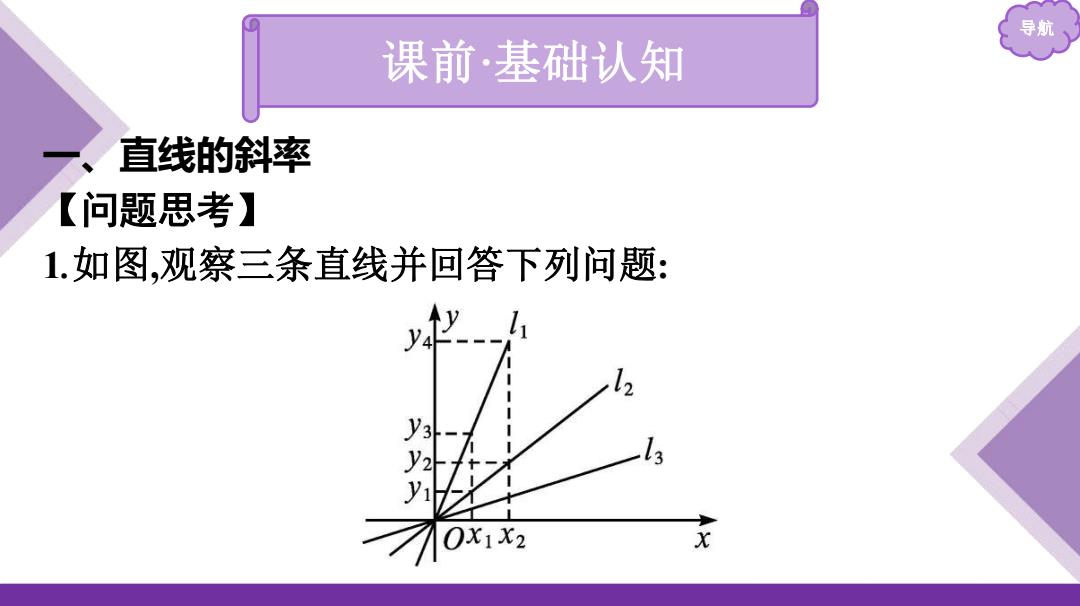
导航 课前·基础认知 直线的斜率 【问题思考】 1.如图,观察三条直线并回答下列问题: 12 13 OX1X2 x
导航 课前·基础认知 一、直线的斜率 【问题思考】 1.如图,观察三条直线并回答下列问题:

导 (1)直观感受一下,图中三条直线中哪条直线最“陡峭”? 提示:直线l1最“陡峭”. (2)如图,对于直线l1和2y2y1和y43哪个大? 提示y4y3大. (3)结合(1)和(2)中的结论,这个结论具有一般意义吗?如何描 述直线的倾斜程度? 提示:(1)和(2)中的结论具有一般意义,用 1描述直线的倾 斜程度
导航 (1)直观感受一下,图中三条直线中哪条直线最“陡峭”? 提示:直线l1最“陡峭” . (2)如图,对于直线l1和l2 ,y2 -y1和y4 -y3哪个大? 提示:y4 -y3大. (3)结合(1)和(2)中的结论,这个结论具有一般意义吗?如何描 述直线的倾斜程度? 提示:(1)和(2)中的结论具有一般意义,用 描述直线的倾 斜程度. 𝒚𝟐-𝒚𝟏 𝒙𝟐-𝒙𝟏

2.填空: (1)直线的斜率:一般地,给定平面直角坐标系中的任意两点 A(c1y1),B(c2y2),当x1x2时,称 Y2Y为直线AB的斜率;当xx X2-X1 时,称直线AB的斜率 (2)直线斜率的几何意义:直线AB的斜率反映了直线相对于x 轴的倾斜程度 (3)直线斜率的其他表示法: 若记Ax,A吗zy,则当A0时,斜率可记为兴
导航 2.填空: (1)直线的斜率:一般地,给定平面直角坐标系中的任意两点 A(x1 ,y1 ),B(x2 ,y2 ),当x1≠x2时,称 为直线AB的斜率;当x1=x2 时,称直线AB的斜率不存在. (2)直线斜率的几何意义:直线AB的斜率反映了直线相对于x 轴的倾斜程度. (3)直线斜率的其他表示法: 𝒚𝟐-𝒚𝟏 𝒙𝟐-𝒙𝟏 若记 Δx=x2-x1,Δy=y2-y1,则当 Δx≠0 时,斜率可记为𝚫𝒚 𝚫𝒙

导航 3.做一做:已知平面直角坐标系中的两点A(2,3),B(-1,4),则直 线AB的斜率是 解析品2号 4-3 答案号
导航 3.做一做:已知平面直角坐标系中的两点A(2,3),B(-1,4),则直 线AB的斜率是 . 解析: 𝟒-𝟑 (-𝟏)-𝟐 =- 𝟏 𝟑 . 答案:- 𝟏 𝟑
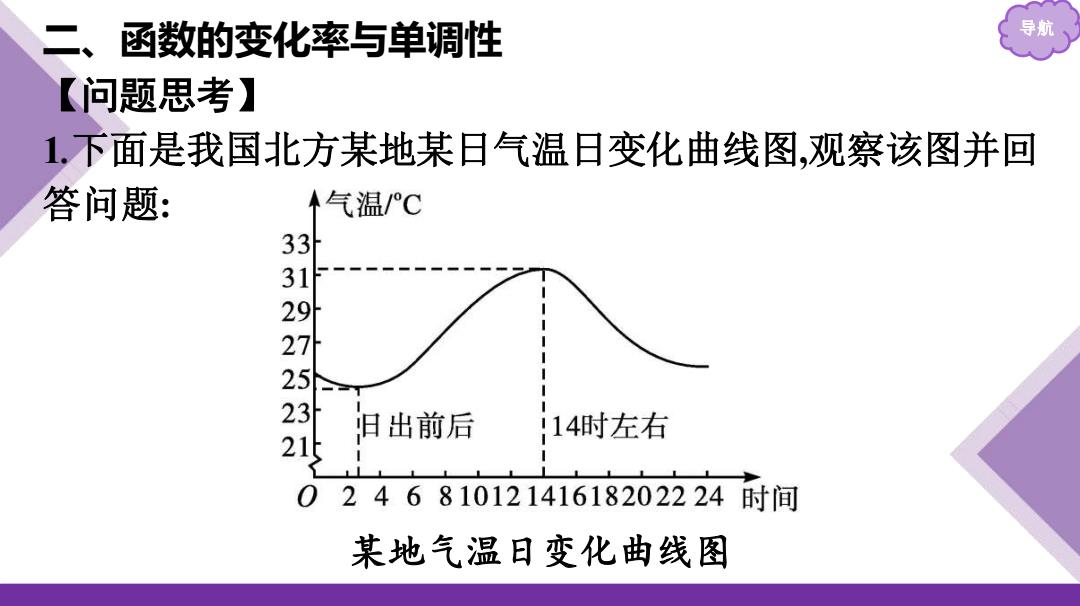
二、函数的变化率与单调性 【问题思考】 1,下面是我国北方某地某日气温日变化曲线图,观察该图并回 答问题: A气温/C 31097531 旧出前后 14时左右 024681012141618202224时间 某地气温日变化曲线图
导航 二、函数的变化率与单调性 【问题思考】 1.下面是我国北方某地某日气温日变化曲线图,观察该图并回 答问题: 某地气温日变化曲线图

)从图上观察,你认为这是哪个季节的气温曲线图?请说明理 由。 提示:夏季的气温曲线图.原因是从气温曲线图上看,一天之中 昼夜温差不是很大,最低气温是24℃左右. (2)从图中可以看出,从6时到10时为“气温陡增”的时段,它的 数学意义是什么? 提示:“气温陡增”是指温度在相同的时间内变化大,即温差大
导航 (1)从图上观察,你认为这是哪个季节的气温曲线图?请说明理 由. 提示:夏季的气温曲线图.原因是从气温曲线图上看,一天之中 昼夜温差不是很大,最低气温是24 ℃左右. (2)从图中可以看出,从6时到10时为“气温陡增”的时段,它的 数学意义是什么? 提示:“气温陡增”是指温度在相同的时间内变化大,即温差大

导 (3)假设6时的气温是25℃,10时的气温是29℃,12时的气温是 30℃,那么如何比较从6时到10时与从10时到12时气温变化的 大小? 提示:从6时到10时的气温变化率为29251, 10-6 从10时到12时的气温变化率为30-29 1 12-10 =2
导航 (3)假设6时的气温是25 ℃,10时的气温是29 ℃,12时的气温是 30 ℃,那么如何比较从6时到10时与从10时到12时气温变化的 大小? 提示:从 6 时到 10 时的气温变化率为𝟐𝟗-𝟐𝟓 𝟏𝟎-𝟔 =1, 从 10 时到 12 时的气温变化率为𝟑𝟎-𝟐𝟗 𝟏𝟐-𝟏𝟎 = 𝟏 𝟐