
全程设计 2.1.1 等式的性质与方程的解集
2.1.1 等式的性质与方程的解集
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解恒等式和方程的解集的概念 2.掌握等式的性质. 3.能使用“十字相乘法”等因式分解的方法求方程的解集 4.体验数学抽象的过程,培养逻辑推理能力和数学运算能力
导航 课标定位素养阐释 1.了解恒等式和方程的解集的概念. 2.掌握等式的性质. 3.能使用“十字相乘法”等因式分解的方法求方程的解集. 4.体验数学抽象的过程,培养逻辑推理能力和数学运算能力

导航 课前·基础认知 等式的性质 【问题思考】 1.阅读下面的语句,判断是否正确 (1)若ac2=bc2,则a=b; (2)若a=b,则ac2=bc2. 提示:(1)不正确.(2)正确. 2.若ac2=bc2,是否一定有ac2+m-n=bc2+m-n(m,n∈R)? 提示:一定有
导航 课前·基础认知 一、等式的性质 【问题思考】 1.阅读下面的语句,判断是否正确. (1)若ac2=bc2 ,则a=b; (2)若a=b,则ac2=bc2 . 提示:(1)不正确.(2)正确. 2.若ac2=bc2 ,是否一定有ac2+m-n=bc2+m-n(m,n∈R)? 提示:一定有
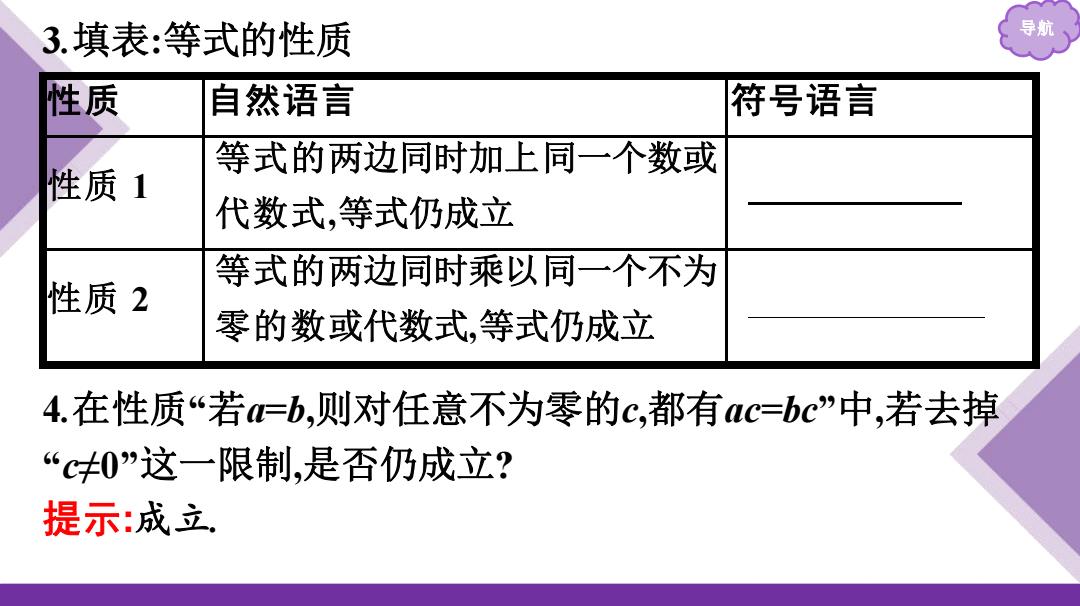
3填表:等式的性质 导航 性质 自然语言 符号语言 等式的两边同时加上同一个数或 性质1 代数式,等式仍成立 等式的两边同时乘以同一个不为 性质2 零的数或代数式,等式仍成立 4.在性质“若=b,则对任意不为零的c,都有a=bc中,若去掉 “c≠0”这一限制,是否仍成立? 提示:成立
导航 3.填表:等式的性质 性 质 自然语言 符号语言 性 质 1 等式的两边同时加上同一个数或 代数式,等式仍成立 a=b⇒a+c=b+c 性 质 2 等式的两边同时乘以同一个不为 零的数或代数式,等式仍成立 a=b,c≠0⇒ac=bc 4.在性质“若a=b,则对任意不为零的c,都有ac=bc”中,若去掉 “c≠0”这一限制,是否仍成立? 提示:成立

导航 5.做一做:下列命题中的真命题有 (填序号) ①若叶n=q,则=q-n; ②若2m=2n,则Fn; 图若m=0,则贤=2 ④若a(p+-1)=bp+-1),则a=b. 答案:①②③
导航 5.做一做:下列命题中的真命题有 .(填序号) ①若m+n=q,则m=q-n; ②若2m=2n,则m=n; ③若 m=n,a≠0,则 𝒎 𝒂 = 𝒏 𝒂 ; ④若a(p+q-1)=b(p+q-1),则a=b. 答案:①②③
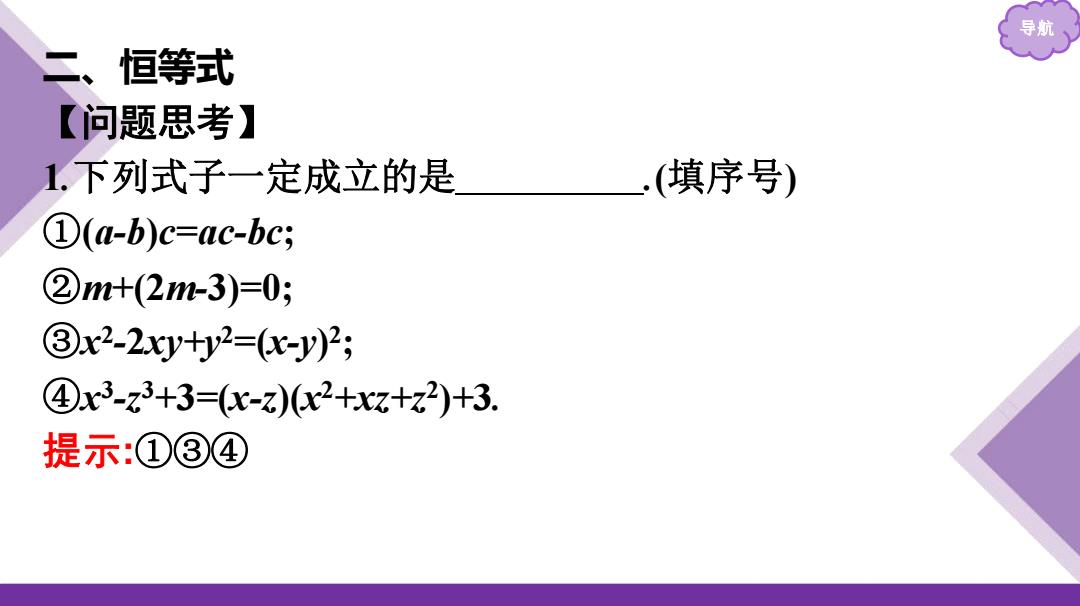
导航 二、恒等式 【问题思考】 1.下列式子一定成立的是 (填序号) ①(a-b)c=c-bc; ②mt(2m-3)=0; ③x2-2xy+y2=(ky)2; ④x3-z3+3=(c-z)x2+xz+z2)+3. 提示:①③④
导航 二、恒等式 【问题思考】 1 .下列式子一定成立的是 . (填序号 ) ① ( a - b )c=ac -bc ; ②m+(2 m -3) =0; ③x 2 - 2xy+y 2 = (x-y ) 2 ; ④x 3 -z 3 + 3 = (x -z)(x2+xz+z 2 ) + 3 . 提示 :①③④

导航 2.填空:(1)一般地,含有字母的等式,如果其中的字母取 时等式都成立,则称其为恒等式,也称等式两边恒等 (2)a2-b2= (a+b)2=a2+b2; (-b)2=2+b2; 3+b3= 3-b3=
导航 2.填空:(1)一般地,含有字母的等式,如果其中的字母取任意实 数时等式都成立,则称其为恒等式,也称等式两边恒等. (2)a 2 -b 2= (a+b)(a-b) ; (a+b) 2=a2 +2ab +b 2 ; (a-b) 2=a2 -2ab +b 2 ; a 3+b3= (a+b)(a 2 -ab+b2 ) ; a 3 -b 3= (a-b)(a 2+ab+b2 )

导航 3做一做:(1)下列选项中,与x能构成恒等式的是( A. B.x2 C.x+1 D 3 答案:D (2)化简:x-2)2-(x+2)2. 解:x-2)2-(K+2)2=[x-2)+(x+2)Ic-2)-(x+2)=2xX(-4)=-8x (或(k-2)2-(x+2)2=(x2-4x+4)-(x2+4x+4)=-8x)
导航 3.做一做:(1)下列选项中,与x能构成恒等式的是( ) A.|x| B.x 2 C.x +1 D. 𝟑𝒙 𝟑 答案:D (2)化简:(x-2)2 -(x+2)2 . 解:(x-2)2 -(x+2)2=[(x-2)+(x+2)][(x-2)-(x+2)]=2x×(-4)=-8x. (或(x-2)2 -(x+2)2=(x 2 -4x+4)-(x 2+4x+4)=-8x)

导航 三、十字相乘法 【问题思考】 1.将下列式子化为x2+Cx+D(C,D∈R)的形式 (1)x+2)x-3); (2)x+1)c+2); (3)x-1)x-2). 提示:(1)x2-x-6.(2)x2+3x+2.(3)x2-3x+2
导航 三、十字相乘法 【问题思考】 1.将下列式子化为x 2+Cx+D(C,D∈R)的形式. (1)(x+2)(x-3); (2)(x+1)(x+2); (3)(x-1)(x-2). 提示:(1)x 2 -x-6.(2)x 2+3x+2.(3)x 2 -3x+2