
全程设计 3.2函数与方程、 不等式之间的关系 第2课时 零点的存在性及其近似值的 求法
3.2 函数与方程、不等式之间的关系 第2课时 零点的存在性及其近似值的 求法
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.理解函数零点存在定理,会判断函数零,点是否存在 2.掌握二分法求函数零点的步骤及原理 3.会用二分法求函数零点的近似值
导航 课标定位素养阐释 1.理解函数零点存在定理,会判断函数零点是否存在. 2.掌握二分法求函数零点的步骤及原理. 3.会用二分法求函数零点的近似值
导航 课前·基础认知 函数零点存在定理 【问题思考】 1.观察下面函数的图象并回答问题: 函数fx)=x2.4x+3的图象如图. (1)函数fx)的零点是什么? 3x 提示:1和3. (2)判断f0f2)与f24)的符号. 提示:.f0)=3f2)=-1,4)=3,0f2)<0,24)<0
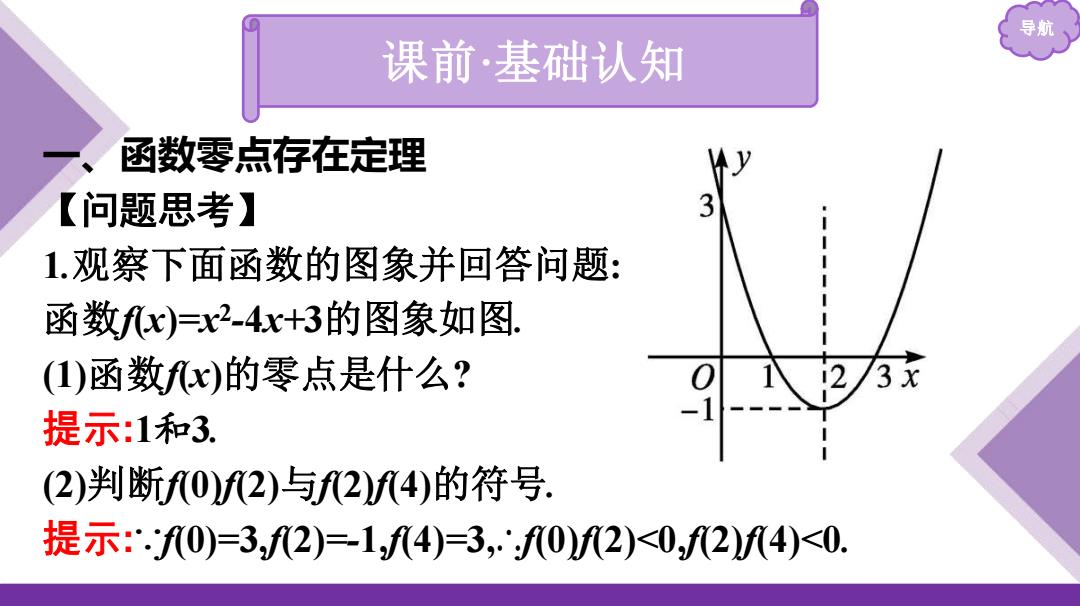
导航 课前·基础认知 一、函数零点存在定理 【问题思考】 1.观察下面函数的图象并回答问题: 函数f(x)=x2 -4x+3的图象如图. (1)函数f(x)的零点是什么? 提示:1和3. (2)判断f(0)f(2)与f(2)f(4)的符号. 提示:∵f(0)=3,f(2)=-1,f(4)=3,∴f(0)f(2)<0,f(2)f(4)<0

导航 2填空: 函数零点存在定理:如果函数y=fx)在区间[,b上的图象是连 续不断的,并且 (即在区间两个端点处的函数值异 号),则函数y=f)在区间(a,b)中至少有一个零点,即x∈(a,b)
导航 2.填空: 函数零点存在定理:如果函数y=f(x)在区间[a,b]上的图象是连 续不断的,并且f(a)f(b)<0 (即在区间两个端点处的函数值异 号),则函数y=f(x)在区间(a,b)中至少有一个零点,即∃x0∈(a,b), f(x0 )=0

3.做一做: (1)若函数y=fx)在区间(a,b)内有零点,则ffb)的符号( A.大于零 B.小于零 C等于零 D.不能确定 (2)若函数fx)=x+在区间(1,2)内有零点,则实数的取值范围 是 解析:1)因为函数fx)=x-1在区间(0,2)内有零点10)f2)0, 所以孔fb)的符号不能确定. (2)由题意,得f1)f2)=(1+)2+0)<0,解得-2<<-1. 答案:(1)D(2)(-2,-1)
导航 3.做一做: (1)若函数y=f(x)在区间(a,b)内有零点,则f(a)f(b)的符号( ) A.大于零 B.小于零 C.等于零 D.不能确定 (2)若函数f(x)=x+a在区间(1,2)内有零点,则实数a的取值范围 是 . 解析:(1)因为函数f(x)=x-1在区间(0,2)内有零点1,f(0)f(2)0, 所以f(a)f(b)的符号不能确定. (2)由题意,得f(1)f(2)=(1+a)(2+a)<0,解得-2<a<-1. 答案:(1)D (2)(-2,-1)

导期 二、二分法 【问题思考】 1.思考并回答问题: ()从机房到用户有一根光缆线,现测得光缆线上有一个断点, 如何尽快找到这个断点? 提示:从中间(中点)向机房测试,若通,则断点必在中点与用户 之间;若不通,则断点在中点与机房之间..以此查找,则能较 快找到断点的大致位置
导航 二、二分法 【问题思考】 1.思考并回答问题: (1)从机房到用户有一根光缆线,现测得光缆线上有一个断点, 如何尽快找到这个断点? 提示:从中间(中点)向机房测试,若通,则断点必在中点与用户 之间;若不通,则断点在中点与机房之间……以此查找,则能较 快找到断点的大致位置

导月 (2)已知函数y=fx)在区间[2,3]上的图象是连续的,且f2)>0, 3)0,则零,点必在区间(2.5,3)内,否则在区间(2,2.5)内 重复上面的步骤即可尽快缩小零点所在区间的范围
导航 (2)已知函数y=f(x)在区间[2,3]上的图象是连续的,且f(2)>0, f(3)0,则零点必在区间(2.5,3)内,否则在区间(2,2.5)内. 重复上面的步骤即可尽快缩小零点所在区间的范围

2.填空: 在函数零点存在定理的条件满足时(即fx)在区间[a,b]上的图 象是 ,且 ),给定近似的精确度ε,用二分 法求零点x的近似值x,使得|x1xo<的一般步骤如下: 第一步 检查b-2是否成立,如果成立,取x1艺,计算结束; 如果不成立,转到第二步 第二步 计算区间a,)的中点对应的函数值,若f尝)0, 取x”,计算结束;若()0,转到第三步
导航 2.填空: 在函数零点存在定理的条件满足时(即f(x)在区间[a,b]上的图 象是 连续不断的,且 f(a)f(b)<0 ),给定近似的精确度ε,用二分 法求零点x0的近似值x1 ,使得| x1 -x0 |<ε的一般步骤如下: 第一步 检查|b-a|<2ε 是否成立,如果成立,取 x1= 𝒂+𝒃 𝟐 ,计算结束; 如果不成立,转到第二步. 第二步 计算区间(a,b)的中点𝒂+𝒃 𝟐 对应的函数值,若 f 𝒂+𝒃 𝟐 =0, 取 x1= 𝒂+𝒃 𝟐 ,计算结束;若 f 𝒂+𝒃 𝟐 ≠0,转到第三步

导航 第三步若()0,将的值赋给_(用 生b表示,下同)回到第一步; 否则必有)))0,将的值赋给一回到第一步
导航 第三步 若 f(a) f 𝒂+𝒃 𝟐 <0,将 𝒂+𝒃 𝟐 的值赋给 b 用 𝒂+𝒃 𝟐 →𝒃表示,下同 ,回到第一步; 否则必有 f 𝒂+𝒃 𝟐 f(b)<0,将 𝒂+𝒃 𝟐 的值赋给 a ,回到第一步