
全程设计 7.1.2 孤度制及其与角度制的换算
7.1.2 弧度制及其与角度制的换算

导航 课标定位素养阐释 1.了解弧度制,能熟练地进行孤度制与角度制之间的换算 2.掌握孤度制中扇形的面积公式 3.加强数学抽象能力和数学运算能力的培养
导航 课标定位 素养阐释 1.了解弧度制,能熟练地进行弧度制与角度制之间的换算. 2.掌握弧度制中扇形的面积公式. 3.加强数学抽象能力和数学运算能力的培养
课前·基础认知 课堂·重难突破 随堂训练 思想方法
思 想 方 法 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 弧度制 【问题思考】 1.如图,在射线OA上有一点M,OA经旋转后得到角a,此时点 M运动的路程为s,路程s与角a有关系吗? M 提示:有s越大,越大
导航 课前·基础认知 一、弧度制 【问题思考】 1.如图,在射线OA上有一点M,OA经旋转后得到角α,此时点 M运动的路程为s,路程s与角α有关系吗? 提示:有.s越大,|α|越大

2.填空:(1)用作单位来度量角的制度称为角度制,规定1°= 60',10" (2)①长度等于半径长的 所对的 为1弧度的角,以 为单位来度量角的制度称为弧度制. ②在半径为r的圆中,若弧长为的弧所对的圆心角为arad, 则
导航 2.填空:(1)用度作单位来度量角的制度称为角度制,规定1° = 60' ,1'= 60″ . (2)①长度等于半径长的圆弧所对的圆心角为1弧度的角,以 弧度为单位来度量角的制度称为弧度制. ②在半径为r的圆中,若弧长为l的弧所对的圆心角为α rad, 则 α= 𝒍 𝒓

导航 3.做一做:在半径为2的圆周上有一段弧的长度为3,则这段弧 所对的圆心角为 rad,圆周角为 rad. 答案
导航 3.做一做:在半径为2的圆周上有一段弧的长度为3,则这段弧 所对的圆心角为 rad,圆周角为 rad. 答案: 𝟑 𝟐 𝟑 𝟒
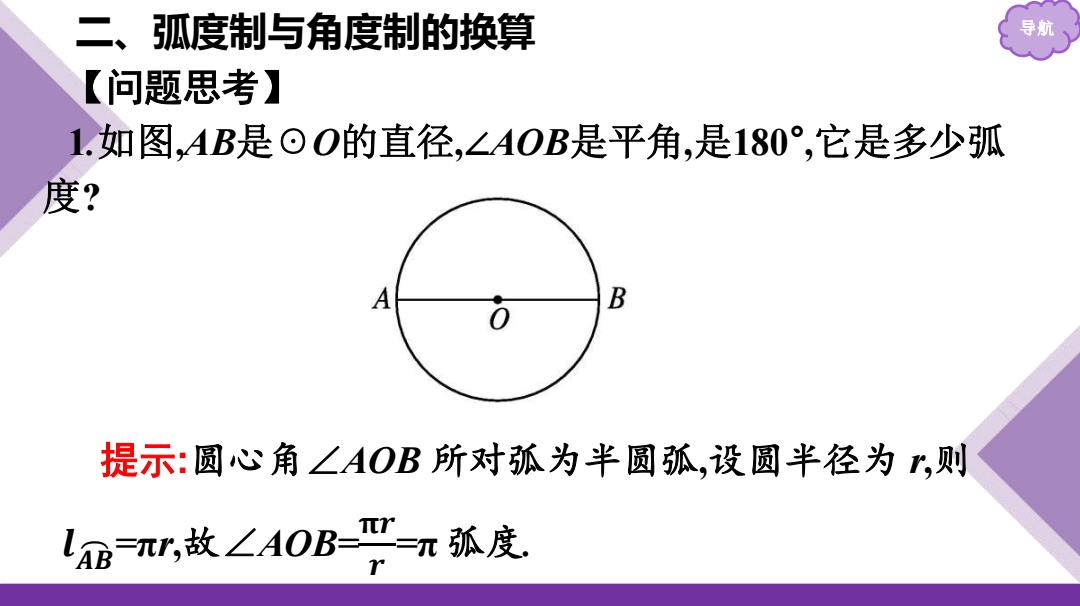
二、弧度制与角度制的换算 导期 【问题思考】 1.如图,AB是⊙O的直径,∠AOB是平角,是180°,它是多少弧 度? B 提示:圆心角∠AOB所对孤为半圆弧,设圆半径为?,则 l=,故∠AOBT=π孤度
二、弧度制与角度制的换算 导航 【问题思考】 1.如图,AB是☉O的直径,∠AOB是平角,是180° ,它是多少弧 度? 提示:圆心角∠AOB 所对弧为半圆弧,设圆半径为 r,则 𝒍 𝑨 𝑩 =πr,故∠AOB=𝛑𝒓 𝒓 =π 弧度

导航 2,填空:(1)设一个角的角度数为m,弧度数为么则180=一 (2)180°=元_ad 3.做一做:(1)120°= rad; 2 答案:( L(2)-60°
导航 2.填空:(1)设一个角的角度数为 n,弧度数为 α,则 𝒏 𝟏𝟖𝟎 = 𝜶 𝛑 . (2)180° = π rad. 3.做一做:(1)120° = rad; (2)- 𝛑 𝟑 = . 答案:(1)𝟐𝛑 𝟑 (2)-60°

导航 三、扇形面积公式 【问题思考】 1已知扇形的弧长为红半径为2,则扇形的面积是多少? 2π 提示:扇形的圆心角为亨= rad=60°, 60元x22_2 故S扇36 2.填空:若扇形的弧长为,半径为,则扇形面积S=
导航 三、扇形面积公式 【问题思考】 1.已知扇形的弧长为 ,半径为2,则扇形的面积是多少? 𝟐𝛑 𝟑 提示:扇形的圆心角为 𝟐𝛑 𝟑 𝟐 = 𝛑 𝟑 rad=60° , 故 S 扇= 𝟔𝟎 𝟑𝟔𝟎 ×π×2 2 = 𝟐𝛑 𝟑 . 2.填空:若扇形的弧长为l,半径为r,则扇形面积S=______. 𝟏 𝟐 lr

导航 3.做一做:已知扇形的圆心角为1rad,半径为1,则扇形面积 解析:扇形的孤长Fa一1x1=1,故S1x1吃 答案号
导航 3.做一做:已知扇形的圆心角为1 rad,半径为1,则扇形面积 S= . 解析:扇形的弧长 l=αr=1×1=1,故 S=𝟏 𝟐 lr=𝟏 𝟐 ×1×1= 𝟏 𝟐 . 答案: 𝟏 𝟐