
全程设计 3.1.2 函数的单调性 第2课时 函数的最大(小)值
3.1.2 函数的单调性 第2课时 函数的最大(小)值
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1理解函数的最大(小)值的概念及其几何意义 2.会借助函数的单调性求最值 3.掌握求二次函数在闭区间上的最值
导航 课标定位素养阐释 1.理解函数的最大(小)值的概念及其几何意义. 2.会借助函数的单调性求最值. 3.掌握求二次函数在闭区间上的最值
导 课前·基础认知 函数的最大值和最小值 2020年10月~2021年9月 【问题思考】 个房价/元/m2) 1.阅读下面的实例并回答 27200 2020年10月 26900 26600 25865元/m2 下列问题: 26300 26000 实例:某市房管局公布的 25700 254005 该市房价走势如图所示 0101112010203040506070809月份
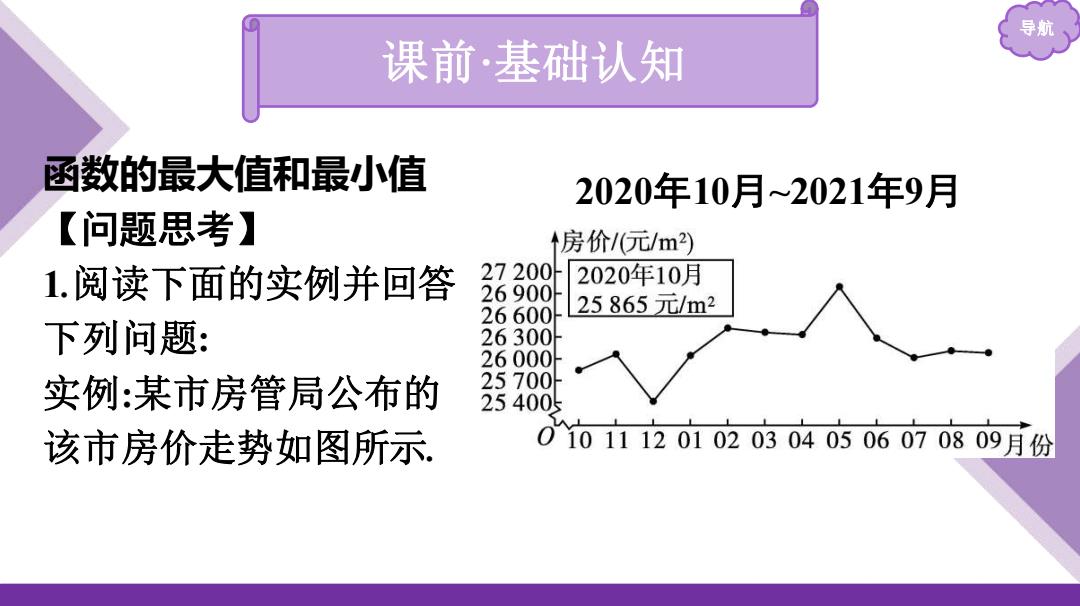
导航 课前·基础认知 函数的最大值和最小值 【问题思考】 1.阅读下面的实例并回答 下列问题: 实例:某市房管局公布的 该市房价走势如图所示. 2020年10月~2021年9月

(1)从图中能否得出该时期房价的最大值和最小值? 提示:从图中可以看到,该时期房价的最大值为2021年5月份 的价格,为26900元m2,而该时期房价的最小值为2020年12月 份的价格,为25400元m2. (2)从走势图上看,2020年10月房价处于上升期,到2020年11月 开始下降,那么2020年11月的房价是该时期的最大值吗?为什 么? 提示:不是.因为该时期房价的最大值应该是所有房价中的最 大者,很明显2020年11月份的房价不满足这个条件,它只是10 月到12月这个局部时期的最大值
导航 (1)从图中能否得出该时期房价的最大值和最小值? 提示:从图中可以看到,该时期房价的最大值为2021年5月份 的价格,为26 900元/m2 ,而该时期房价的最小值为2020年12月 份的价格,为25 400元/m2 . (2)从走势图上看,2020年10月房价处于上升期,到2020年11月 开始下降,那么2020年11月的房价是该时期的最大值吗?为什 么? 提示:不是.因为该时期房价的最大值应该是所有房价中的最 大者,很明显2020年11月份的房价不满足这个条件,它只是10 月到12月这个局部时期的最大值

(3)对于一个函数fx),x∈D,如果实数M是它的最大值,那么对" 任意的x∈D,fx)和M的大小关系是怎样的? 提示:对任意的x∈D,fx)≤M. (4)对于函数fx)=-x2如果fx)≤2恒成立,那么2是函数fx)=-2 的最大值吗?这说明什么问题? 提示:不是这说明函数的最大值必须是函数的其中一个函数 值. (⑤)总结函数最大值M需满足的条件,你能得到函数fx),x∈D 的最小值m需满足的条件吗? 提示:能.对任意的x∈D,fx)≥,且m是函数fx)的一个函数值
导航 (3)对于一个函数f(x),x∈D,如果实数M是它的最大值,那么对 任意的x∈D,f(x)和M的大小关系是怎样的? 提示:对任意的x∈D,f(x)≤M. (4)对于函数f(x)=-x 2 ,如果f(x)≤2恒成立,那么2是函数f(x)=-x 2 的最大值吗?这说明什么问题? 提示:不是.这说明函数的最大值必须是函数的其中一个函数 值. (5)总结函数最大值M需满足的条件,你能得到函数f(x),x∈D 的最小值m需满足的条件吗? 提示:能.对任意的x∈D,f(x)≥m,且m是函数f(x)的一个函数值

导航 2.填空: 一 般地,设函数fx)的定义域为D,且x∈D: ()如果对任意x∈D,都有 ,则称fx)的最大值为fx), 而称为x)的最大值点; (2)如果对任意x∈D,都有 ,则称fx)的最小值为f), 而称为fx)的最小值点 (3)】 统称为最值, 统称为 最值点
导航 2.填空: 一般地,设函数f(x)的定义域为D,且x0∈D: (1)如果对任意x∈D,都有 f(x)≤f(x0 ) ,则称f(x)的最大值为f(x0 ), 而 x0 称为f(x)的最大值点; (2)如果对任意x∈D,都有 f(x)≥f(x0 ) ,则称f(x)的最小值为f(x0 ), 而 x0 称为f(x)的最小值点. (3)最大值和最小值统称为最值,最大值点和最小值点统称为 最值点
3.做一做:(1)如图,函数y=fx)x∈【4,7刀的最大值为 ,最 会航 大值点为 ,最小值为,最小值点为 3 y=f(x) 2 1 -1.5 4 -3引-2-10 234 5 6 7 2 (2)函数fx)=x,x∈-3,2的最大值为,最小值为
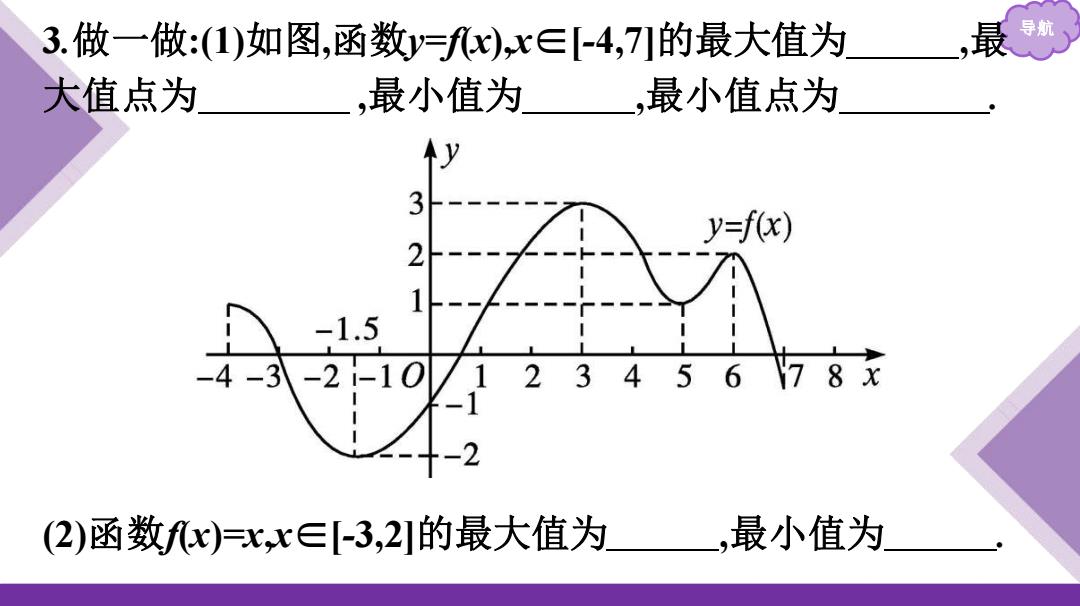
导航 3.做一做:(1)如图,函数y=f(x),x∈[-4,7]的最大值为 ,最 大值点为 ,最小值为 ,最小值点为 . (2)函数f(x)=x,x∈[-3,2]的最大值为 ,最小值为

导 解析:1)由题图可知,函数图象的最高点的坐标为(3,3),所以其 最大值为3,最大值点为3;函数图象的最低点的坐标为(1.5,-2), 所以其最小值为-2,最小值点为-1.5 (2)因为函数fx)=x在区间[-3,2]上单调递增,所以函数fx)的最 大值为2)=2,最小值为f-3)=3. 答案:1)33-2-1.5(2)2-3
导航 解析:(1)由题图可知,函数图象的最高点的坐标为(3,3),所以其 最大值为3,最大值点为3;函数图象的最低点的坐标为(-1.5,-2), 所以其最小值为-2,最小值点为-1.5. (2)因为函数f(x)=x在区间[-3,2]上单调递增,所以函数f(x)的最 大值为f(2)=2,最小值为f(-3)=-3. 答案:(1)3 3 -2 -1.5 (2)2 -3

【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√,错误 的画“X” (1)任何函数x)都有最大值和最小值.(×) (2)若存在实数m,使fx)≥m,则m是函数fx)的最小值.(×) 3)若函数fx)在区间[,b]上是增函数,则fx)在区间[a,b]上的 最小值是f孔,最大值是b).(√) (4)如果fx)的最大值、最小值分别为M,m,那么fx)的值域为 [m,M.(×)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)任何函数f(x)都有最大值和最小值.( ) (2)若存在实数m,使f(x)≥m,则m是函数f(x)的最小值.( ) (3)若函数f(x)在区间[a,b]上是增函数,则f(x)在区间[a,b]上的 最小值是f(a),最大值是f(b).( ) (4)如果f(x)的最大值、最小值分别为M,m,那么f(x)的值域为 [m,M].( ) × × √ ×