
全程设计 3.1.3 函数的奇偶性 第2课时 函数奇偶性的应用
3.1.3 函数的奇偶性 第2课时 函数奇偶性的应用
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.会应用奇、偶函数图象的对称性解决简单问题, 2.理解奇偶性对单调性的影响,并能综合应用奇偶性与单调性 解决简单的问题 3.理解函数奇偶性的推广一对称性,并能应用函数图象的对 称性解决简单的问题
导航 课标定位素养阐释 1.会应用奇、偶函数图象的对称性解决简单问题. 2.理解奇偶性对单调性的影响,并能综合应用奇偶性与单调性 解决简单的问题. 3.理解函数奇偶性的推广——对称性,并能应用函数图象的对 称性解决简单的问题
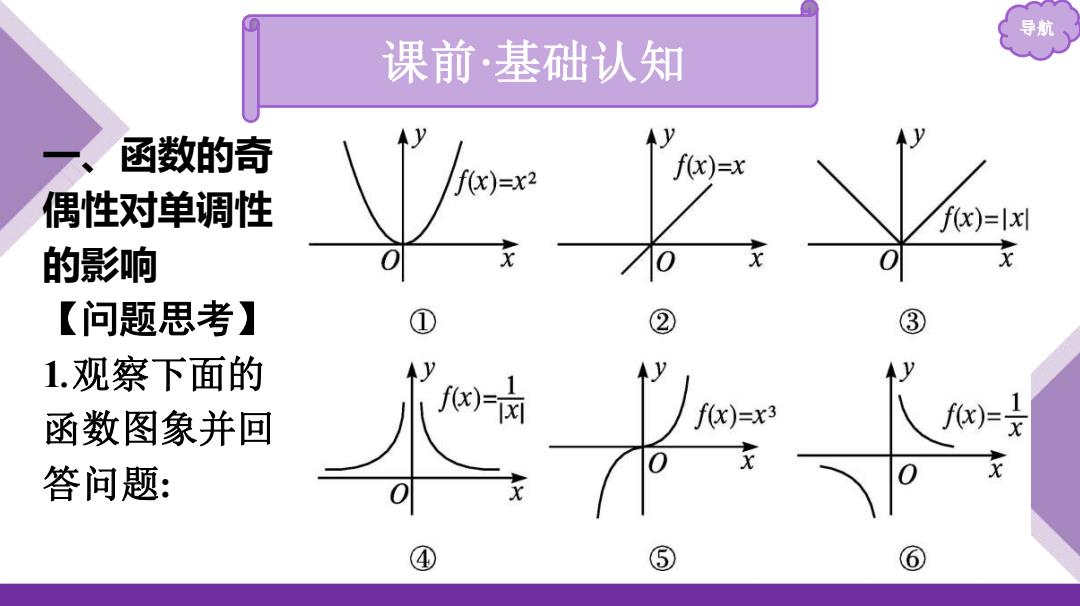
导航 课前·基础认知 函数的奇 f(x)=x2 f(x)=x 偶性对单调性 f(x)=x 的影响 【问题思考】 ① ③ 1.观察下面的 y 函数图象并回 /Q)=x fx)=文 答问题: ④ ⑤ ⑥
导航 课前 ·基础认知 一、函数的奇 偶性对单调性 的影响 【问题思考】 1 .观察下面 的 函数图象并 回 答问 题 :

(1)根据函数的图象指出上面六个函数的奇偶性 导航 提示:①③④中的函数是偶函数,②⑤⑥中的函数是奇函数 (2)指出①③④中函数的单调性 提示: 单调区间 (-00,0) 0,+oo) ①fx)=x2 减函数 增函数 ③fx)= 减函数 增函数 ④w日 增函数 减函数
导航 (1)根据函数的图象指出上面六个函数的奇偶性. 提示:①③④中的函数是偶函数,②⑤⑥中的函数是奇函数. (2)指出①③④中函数的单调性. 提示: 单调区间 (-∞,0) (0,+∞) ①f(x)=x2 减函数 增函数 ③f(x)=|x| 减函数 增函数 ④f(x)= 𝟏 |𝐱| 增函数 减函数
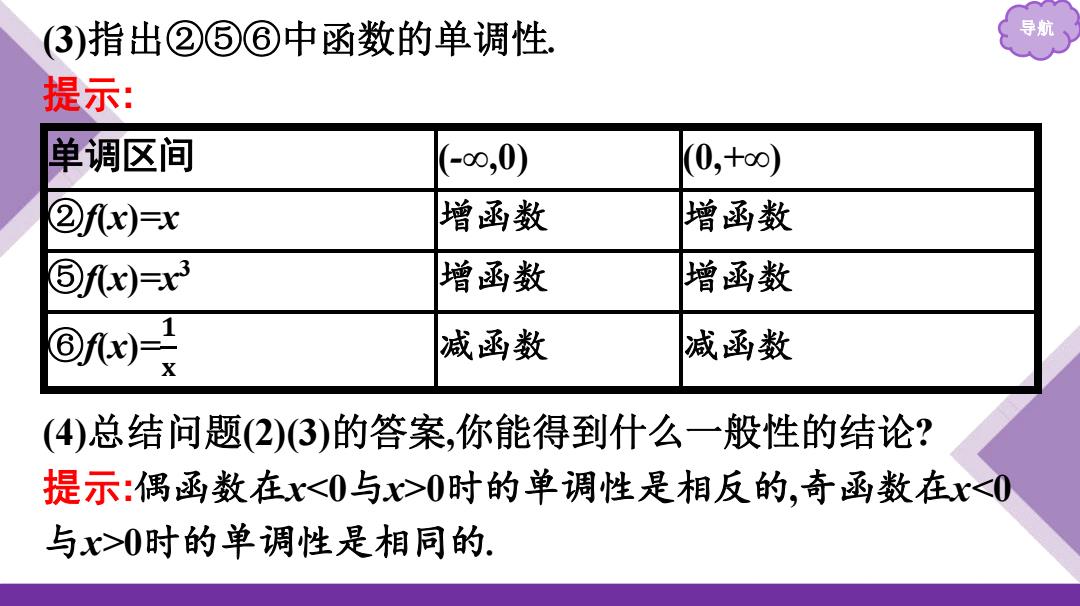
(3)指出②⑤⑥中函数的单调性 导航 提示: 单调区间 (-00,0) (0,+oo) ②fx)=x 增函数 增函数 ⑤fx)=x3 增函数 增函数 @w日 减函数 减函数 (4)总结问题(2)3)的答案,你能得到什么一般性的结论? 提示:偶函数在x0时的单调性是相反的,奇函数在x0时的单调性是相同的
导航 (3)指出②⑤⑥中函数的单调性. 提示: 单调区间 (-∞,0) (0,+∞) ②f(x)=x 增函数 增函数 ⑤f(x)=x3 增函数 增函数 ⑥f(x)= 𝟏 𝐱 减函数 减函数 (4)总结问题(2)(3)的答案,你能得到什么一般性的结论? 提示:偶函数在x0时的单调性是相反的,奇函数在x0时的单调性是相同的

导航 2.填空:(1)如果函数y=fx)是偶函数,那么其在区间[,b]与[-b, -(或(-o,0)与(0,+∞)上的单调性 (2)如果函数y=fx)是奇函数,那么其在区间[a,b]与-b,-(或 (-o,0)与(0,+∞)上的单调性
导航 2.填空:(1)如果函数y=f(x)是偶函数,那么其在区间[a,b]与[-b, -a](或(-∞,0)与(0,+∞))上的单调性相反. (2)如果函数y=f(x)是奇函数,那么其在区间[a,b]与[-b,-a](或 (-∞,0)与(0,+∞))上的单调性相同

导航 3.做一做:(1)已知定义在R上的偶函数y=fx)在区间(0,+o)内 单调递增,则1)与f孔3)的大小关系是 (2)已知y=fx)是定义在R上的奇函数,且在区间(-o,0)内单调 递减.若fc-1)>f1),则x的取值范围是
导航 3.做一做:(1)已知定义在R上的偶函数y=f(x)在区间(0,+∞)内 单调递增,则f(-1)与f(-3)的大小关系是 . (2)已知y=f(x)是定义在R上的奇函数,且在区间(-∞,0)内单调 递减.若f(x-1)>f(1),则x的取值范围是

导航 解析:1)(方法一)因为y=fx)在区间(0,+o)内单调递增,且y= 是偶函数,所以y=x)在区间(oo,0)内单调递减,所以孔-1)f1)等价于x1<1,解得x<2. 答案:(1)f-1)f-3)(2)(-o,2)
导航 解析:(1)(方法一)因为y=f(x)在区间(0,+∞)内单调递增,且y=f(x) 是偶函数,所以y=f(x)在区间(-∞,0)内单调递减,所以f(-1)f(1)等价于x-1<1,解得x<2. 答案:(1)f(-1)<f(-3) (2)(-∞,2)

二、函数图象的对称性 导航 【问题思考】 1,已知二次函数fx)=x24x, (1)函数x)=x24x图象的对称轴是什么? 提示:直线x=2 (2)对任意的实数h,是否都有f2-)=f2+)成立? 提示:是, (3)若函数y=g(c)对任意的实数,都有g(2-h)=g(2+h),则y=g8 的图象的对称轴是什么? 提示:直线x=2
导航 二、函数图象的对称性 【问题思考】 1.已知二次函数f(x)=x2 -4x, (1)函数f(x)=x2 -4x图象的对称轴是什么? 提示:直线x=2. (2)对任意的实数h,是否都有f(2-h)=f(2+h)成立? 提示:是. (3)若函数y=g(x)对任意的实数h,都有g(2-h)=g(2+h),则y=g(x) 的图象的对称轴是什么? 提示:直线x=2