
全程设计 2.向量的数量积与三角恒等变换
2.向量的数量积与三角恒等变换
梳理•构建体系 归纳核心突破 高考体验
梳理•构建体系 归纳•核心突破 高 考 体 验

导航 梳理构建体系 知识网络 (定义:a,b为非零向量,ab=al-Iblcose88为a,b的夹角) 性质:a⊥b=ab=0:a,b同向,ab=lal-lbl:a,b反向, a-b -la 运算律:ab=ba,(aab=a(b).a+bc=ac+bc 向量的数量积 向量的模:设a=(x,y),则回=√x2+y2 a=(x1.y1).b =(xz.y2).cos a.b>= X1x2+yy2 好+x好+y 向量的数量积与三角恒等变换 ab =x1x2 +yiy2 两角和差的余弦:cos(a士B)=cosacosB干sinasinB 和差角公式 两角和差的正弦:sin(a士B)=sinacos3±cosasinB 两角和差的正切:tan(a土)= tana±tanβ 1干tanatanB T倍角的正弦、余弦、正切:sin2a=2 sinacosa cos2a cos2a-sin2a 2cos2a-1 1-2sin2a, 三角恒等变换 倍半角公式 2tang tan2a 1-tan2a 半角的正弦、余弦、正切 和差与积互化 「和差化积 积化和差 b 辅助角公式:asinx+bcosx=√a2+b2sin(x+p),其中tanp= Q
导航 梳理 •构建体系 知识网络 向量的数量积 定义:𝑎,𝑏为非零向量,𝑎·𝑏 = |𝑎|·|𝑏|cos𝜃(𝜃为𝑎,𝑏的夹角) 性质:𝑎 ⊥ 𝑏⇔𝑎·𝑏 = 0;𝑎,𝑏同向,𝑎·𝑏 = |𝑎|·|𝑏|;𝑎,𝑏反向, 𝑎·𝑏 = -|𝑎|·|𝑏| 运算律:𝑎·𝑏 = 𝑏·𝑎,(𝜆𝑎)·𝑏 = 𝑎·(𝜆𝑏),(𝑎 + 𝑏)·𝑐 = 𝑎·𝑐 + 𝑏·𝑐 向量的模:设𝑎 = (𝑥,𝑦),则|𝑎| = 𝑥2 + 𝑦2 设𝑎 = (𝑥1,𝑦1 ),𝑏 = (𝑥2,𝑦2 ),cos = 𝑥1𝑥2 + 𝑦1𝑦2 𝑥12 + 𝑦12· 𝑥22 + 𝑦22 , 𝑎·𝑏 = 𝑥1𝑥2 + 𝑦1𝑦2 三角恒等变换 和差角公式 两角和差的余弦:cos(𝛼 ± 𝛽) = cos 𝛼cos 𝛽 ∓sin 𝛼sin 𝛽 两角和差的正弦:sin(𝛼 ± 𝛽) = sin 𝛼cos 𝛽 ± cos 𝛼sin 𝛽 两角和差的正切:tan(𝛼 ± 𝛽) = tan 𝛼 ± tan 𝛽 1∓tan𝛼tan𝛽 倍半角公式 倍角的正弦、余弦、正切:sin2 𝛼 = 2sin 𝛼cos 𝛼, cos2 𝛼 = cos2𝛼-sin2𝛼 = 2cos2𝛼-1 = 1-2sin2𝛼, tan2 𝛼 = 2tan 𝛼 1-tan2𝛼 半角的正弦、余弦、正切 和差与积互化 和差化积 积化和差 辅助角公式:𝑎sin𝑥 + 𝑏cos𝑥 = 𝑎2 + 𝑏2sin(𝑥 + 𝜑),其中 tan 𝜑 = 𝑏𝑎

导航 要点梳理 1.两个向量夹角的范围是什么? 提示:0s<a,b≤元. 2.两个向量a,b的数量积的几何意义是什么? 提示:两个非零向量a,b的数量积ab,等于a(或b)在向量b(或a) 上的投影的数量与b(或a)的模的乘积. 3.两向量垂直的坐标表示是怎样的? 提示:若a=(c1y1),b=(2y2),则a⊥b台x1X2+yy2=0
导航 要点梳理 1.两个向量夹角的范围是什么? 提示:0≤≤π. 2.两个向量a,b的数量积的几何意义是什么? 提示:两个非零向量a,b的数量积a·b,等于a(或b)在向量b(或a) 上的投影的数量与b(或a)的模的乘积. 3.两向量垂直的坐标表示是怎样的? 提示:若a=(x1 ,y1 ),b=(x2 ,y2 ),则a⊥b⇔x1x2+y1 y2 =0
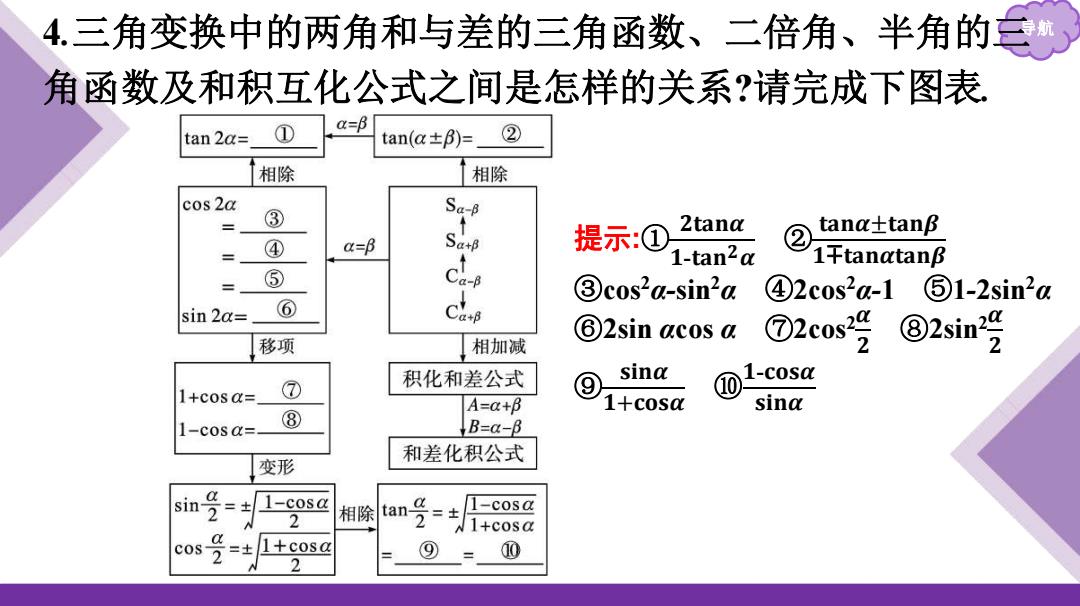
4.三角变换中的两角和与差的三角函数、二倍角、半角的三航 角函数及和积互化公式之间是怎样的关系?请完成下图表, ① a=B tan 2a= tan(a±f)= ② 相除 相除 cos 2a ③ Sa-B 提示:① 2tana ④ a=B ② tana±tanB cd 1-tan2a 1千tangtanβ = ⑤ ③cos2a-sin2a ④2c0s2a-1 ⑤1-2sin2a sin 2a= ⑥ ⑥2 sin acos a 移项 相加减 ⑦2c0s号 ⑧2sim号 积化和差公式 sina ⑩ -c0s 1+cosa= ⑦ A=a+B 1+c0S sing 1-cosa= ⑧ B=a-B 和差化积公式 变形 a sin= 1-cosa 相除 tan之=主人 -cosa 2 1+cosa cos 2 = 1+cosa ⑨ 0 2
导航 4.三角变换中的两角和与差的三角函数、二倍角、半角的三 角函数及和积互化公式之间是怎样的关系?请完成下图表. 提示:① 𝟐𝐭𝐚𝐧𝜶 𝟏-𝐭𝐚𝐧𝟐 𝜶 ② 𝐭𝐚𝐧𝜶±𝐭𝐚𝐧𝜷 𝟏∓𝐭𝐚𝐧𝜶𝐭𝐚𝐧𝜷 ③cos2 α-sin2 α ④2cos2 α-1 ⑤1-2sin2 α ⑥2sin αcos α ⑦2cos2 𝜶 𝟐 ⑧2sin2 𝜶 𝟐 ⑨ 𝐬𝐢𝐧𝜶 𝟏+𝐜𝐨𝐬𝜶 ⑩ 𝟏-𝐜𝐨𝐬𝜶 𝐬𝐢𝐧𝜶

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” (1)a与b的数量积不可能是一个向量.( (2)当ab=0时,a,b中至少有一个是0.( 3)存在与任何向量都平行的向量,也存在与任何向量都垂直 的向量.( (4)a(bc)是一个实数() (5)cos(a+p)=cos acos B+sin asin B.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)a与b的数量积不可能是一个向量.( √ ) (2)当a·b=0时,a,b中至少有一个是0.( × ) (3)存在与任何向量都平行的向量,也存在与任何向量都垂直 的向量.( √ ) (4)a(b·c)是一个实数.( × ) (5)cos(α+β)=cos αcos β+sin αsin β.( × )

导航 1+c0s (6)cos2a= 2 (⑧y=3sin(2x+)+4cos(2x+)可以取到最大值7.( )
导航 (6)cos2 α= 𝟏+𝐜𝐨𝐬 𝜶 𝟐 𝟐 .( × ) (7)tan 𝜶 𝟐 = 𝐬𝐢𝐧𝜶 𝟏-𝐜𝐨𝐬𝜶 .( × ) (8)y=3sin 𝟐𝒙 + 𝛑 𝟒 +4cos 𝟐𝒙 + 𝛑 𝟒 可以取到最大值 7.( × )

导航 归纳•核心突破 专题整合 专题一向量的数量积 【例1】己知非零向量a,b满足(a+b)⊥(2a-b),(a-2b)⊥(2a+b), 求a,b的夹角的余弦值, 分析:由(a+b)L(2a-b),(a-2b)⊥(2a+b)列出方程组→求出|a2, b2,ab的关系→利用夹角公式可求
导航 归纳•核心突破 专题整合 专题一 向量的数量积 【例1】已知非零向量a,b满足(a+b)⊥(2a-b),(a-2b)⊥(2a+b), 求a,b的夹角的余弦值. 分析:由(a+b)⊥(2a-b),(a-2b)⊥(2a+b)列出方程组→求出|a| 2 , |b| 2 ,a·b的关系→利用夹角公式可求

导航、 解:由 21a2-b12+ab=0, 2|a2-2b2-3ab=0, 解得a=ab, 5 (b2=-4ab, 所以ab=-V10ab, 设a与b的夹角为0, 则cos0a的 V10 1ab10
导航 解:由 𝟐|𝒂| 𝟐 -|𝒃| 𝟐 + 𝒂·𝒃 = 𝟎, 𝟐|𝒂| 𝟐 -𝟐|𝒃| 𝟐 -𝟑𝒂·𝒃 = 𝟎, 解得 |𝒂| 𝟐 = - 𝟓 𝟐 𝒂·𝒃, |𝒃| 𝟐 = -𝟒𝒂·𝒃, 所以|a||b|=-√𝟏𝟎a·b, 设 a 与 b 的夹角为 θ, 则 cos θ= 𝒂·𝒃 |𝒂||𝒃| =- √𝟏𝟎 𝟏𝟎

导期 反思感悟 1求两个向量的夹角主要利用两个公式: ab 求解的前提是求出这两个向量的数量积和模 x1x2+y1y2= 2e6子++月 求解的前提是求出两个向量的坐标 2.解决垂直问题,其关键在于将问题转化为向量的数量积为零, 与求夹角一样,若向量能用坐标表示,则将它转化为 x水2yy2=0”较为简单
导航 反思感悟 1.求两个向量的夹角主要利用两个公式: (1)cos θ= 𝒂·𝒃 |𝒂||𝒃| ,求解的前提是求出这两个向量的数量积和模. (2)cos θ= 𝒙𝟏 𝒙𝟐 +𝒚𝟏 𝒚𝟐 𝒙𝟏 𝟐 +𝒚𝟏 𝟐 𝒙𝟐 𝟐 +𝒚𝟐 𝟐 ,求解的前提是求出两个向量的坐标. 2.解决垂直问题,其关键在于将问题转化为向量的数量积为零, 与求夹角一样,若向量能用坐标表示,则将它转化为 “x1x2+y1 y2 =0”较为简单