
全程设计 3.2 函数与方程、不等式之间的关系 第1课时 函数的零点、二次函数的零 点及其与对应方程、不等式解集之间的 关系
3.2 函数与方程、不等式之间的关系 第1课时 函数的零点、二次函数的零 点及其与对应方程、不等式解集之间的 关系
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1理解函数零点的概念. 2.会求一次函数、二次函数的零,点 3.了解二次函数的零点及其对应方程、不等式的解集之间的 关系
导航 课标定位素养阐释 1.理解函数零点的概念. 2.会求一次函数、二次函数的零点. 3.了解二次函数的零点及其对应方程、不等式的解集之间的 关系
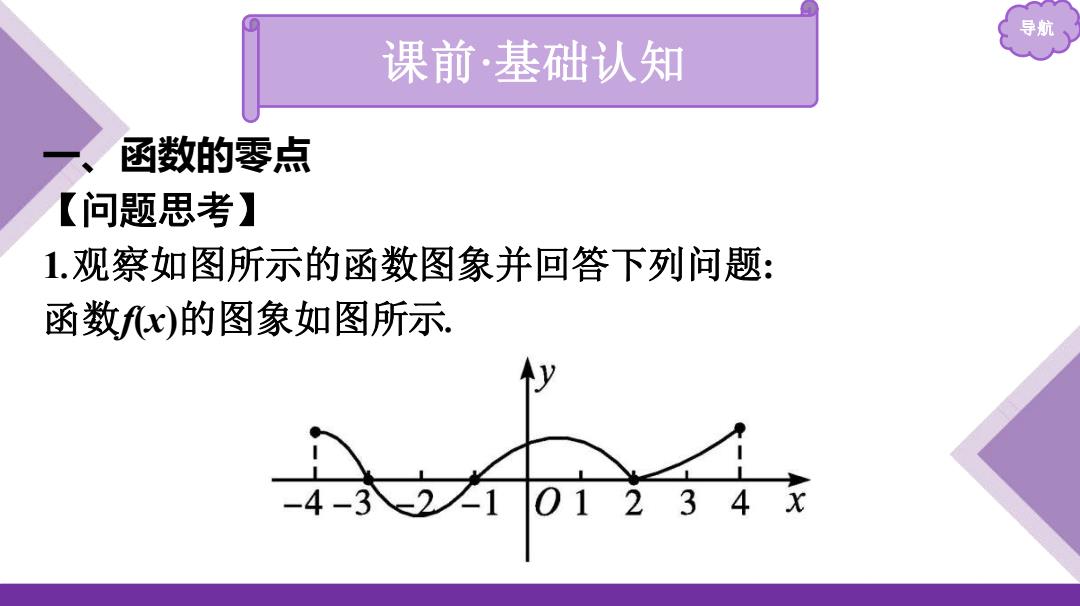
导航 课前·基础认知 函数的零点 【问题思考】 1.观察如图所示的函数图象并回答下列问题: 函数fx)的图象如图所示 -4-3 2Z101234x
导航 课前·基础认知 一、函数的零点 【问题思考】 1.观察如图所示的函数图象并回答下列问题: 函数f(x)的图象如图所示

导 ()根据函数fx)的图象,你能否得出方程fx)=0的根的个数? 提示:方程fx)=O的根即为函数fx)的图象与x轴交点的横坐标 由题图可知,方程fx)=0有3个根,即x=3,-1,2. (2)你认为方程的根与对应函数的图象有什么关系? 提示:方程的根是使函数值等于零的自变量的值,也就是函数 的图象与x轴交点的横坐标
导航 (1)根据函数f(x)的图象,你能否得出方程f(x)=0的根的个数? 提示:方程f(x)=0的根即为函数f(x)的图象与x轴交点的横坐标. 由题图可知,方程f(x)=0有3个根,即x=-3,-1,2. (2)你认为方程的根与对应函数的图象有什么关系? 提示:方程的根是使函数值等于零的自变量的值,也就是函数 的图象与x轴交点的横坐标

导航 2填空: (1)零点的定义:一般地,如果函数y=fx)在实数a处的函数值等 于,即 ,则称a为函数y=fx)的零点 (2)a是函数fx)零点的充分必要条件是,(α,0)是函数图象与 的公共点
导航 2.填空: (1)零点的定义:一般地,如果函数y=f(x)在实数α处的函数值等 于零,即 f(α)=0 ,则称α为函数y=f(x)的零点. (2)α是函数f(x)零点的充分必要条件是,(α,0)是函数图象与 x轴 的公共点
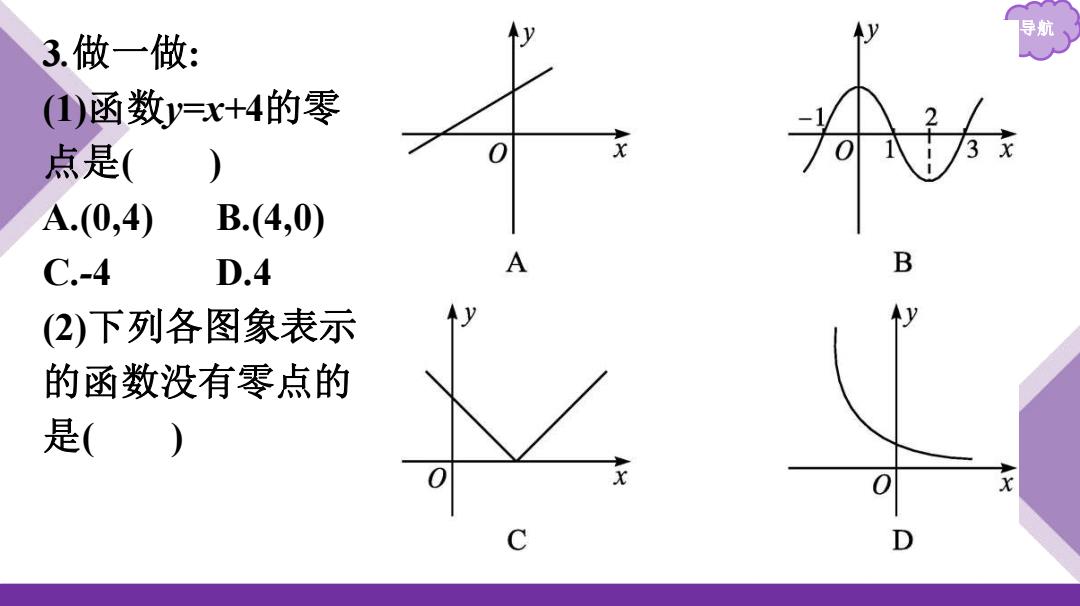
3.做一做: (1)函数y=x+4的零 点是( A.(0,4) B.(4,0) C.-4 D.4 A (2)下列各图象表示 的函数没有零点的 是() X C D
导航 3 .做一做 : (1)函数y=x+ 4的零 点是 ( ) A.(0,4) B.(4,0) C.-4 D.4 (2)下列各图象表示 的函数没有零点的 是( )

导航、 解析:1)令x+4=0,得x=-4,所以函数的零点为-4, (2)因为选项D中的函数图象与x轴没有公共点, 所以其表示的函数没有零,点 答案:1)C(2)D
导航 解析:(1)令x+4=0,得x=-4,所以函数的零点为-4. (2)因为选项D中的函数图象与x轴没有公共点, 所以其表示的函数没有零点. 答案:(1)C (2)D

导 二、二次函数的零点及其与对应方程、不等式解集之间的关 系 【问题思考】 1.考查下列一元二次方程与对应的二次函数: ①方程x2-2x-3=0与函数y=x2-2x-3; ②方程x2-2x+1=0与函数y=x2-2x+1; ③方程x2-2x+3=0与函数y=x2-2x+3
导航 二、二次函数的零点及其与对应方程、不等式解集之间的关 系 【问题思考】 1.考查下列一元二次方程与对应的二次函数: ①方程x 2 -2x-3=0与函数y=x2 -2x-3; ②方程x 2 -2x+1=0与函数y=x2 -2x+1; ③方程x 2 -2x+3=0与函数y=x2 -2x+3

()请列表表示出方程的根、函数的图象及图象与x轴交点的航 坐标 提示: 方程 x2-2x-3=0 x2.2x+1=0 c2-2x+3=0 函数 y=x2-2x-3 y=x2-2x+1 y=x2-2x+3 y y 2 函数的 1 o 图象 -123x 2 -2 -10123x 1 -10123x
导航 (1)请列表表示出方程的根、函数的图象及图象与x轴交点的 坐标. 提示: 方程 x 2 -2x-3=0 x 2 -2x+1=0 x 2 -2x+3=0 函数 y=x2 -2x-3 y=x2 -2x+1 y=x2 -2x+3 函数的 图象