
全程设计 2.2.1 不等式及其性质 第2课时 与不等式性质有关的证明问题
2.2.1 不等式及其性质 第2课时 与不等式性质有关的证明问题
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解证明不等式常用的方法:作差法、综合法、分析法和 反证法. 2.能够灵活选择方法证明一些简单的不等式 3.注重数学运算和逻辑推理能力的培养
导航 课标定位素养阐释 1.了解证明不等式常用的方法:作差法、综合法、分析法和 反证法. 2.能够灵活选择方法证明一些简单的不等式. 3.注重数学运算和逻辑推理能力的培养

导航 课前·基础认知 综合法 【问题思考】 1.能否借助a2-2ab+b2=(a-b)2证明不等式2+b2≥2ab? 提示:能..(a-b)2=2-2ab+b2≥0,.2+b2≥2ab. 2.填空:从 出发,综合利用各种结果,经过逐步推导最 后得到结论的方法,在数学中通常称为综合法
导航 课前·基础认知 一、综合法 【问题思考】 1.能否借助a 2 -2ab+b2=(a-b) 2证明不等式a 2+b2≥2ab? 提示:能.∵(a-b) 2=a2 -2ab+b2≥0,∴a 2+b2≥2ab. 2.填空:从已知条件出发,综合利用各种结果,经过逐步推导最 后得到结论的方法,在数学中通常称为综合法

导航 3已知a>么0,求证>君 证明:.心b,∴.b-清 ●
导航 3.已 知 a>b,ab 𝟏 𝒃 . 证 明:∵a>b,∴b-a0 ,即 𝟏 𝒂 > 𝟏 𝒃

导期 二、反证法 【问题思考】 1.对于2+b2与2ab,如果我们能证明a2+b2<2ab不成立,那么是 否说明2+b2≥2b一定成立? 提示:是此处应用的是命题与其否定p必一真一假的原理 2.填空:首先假设 成立,然后由此进行推理得到 ,最后得出不成立这种得到数学结论的方法通常称 为反证法
导航 二、反证法 【问题思考】 1.对于a 2+b2与2ab,如果我们能证明a 2+b2<2ab不成立,那么是 否说明a 2+b2≥2ab一定成立? 提示:是.此处应用的是命题p与其否定¬p必一真一假的原理. 2.填空:首先假设结论的否定成立,然后由此进行推理得到 矛盾,最后得出假设不成立.这种得到数学结论的方法通常称 为反证法

3.用反证法证明问题时,通常会得到哪些矛盾? 提示:与已知事实矛盾,与公理、定理、定义矛盾,与题设矛盾 等 4.已知0,用反证法证明√1+0,.1+0, (W1+刘2≥(1+),即1+x≥1+x≤0. 这与心0矛盾,假设不成立1+<1+之
导航 3.用反证法证明问题时,通常会得到哪些矛盾? 提示:与已知事实矛盾,与公理、定理、定义矛盾,与题设矛盾 等. 4.已 知 x>0,用反证法证明: 𝟏 + 𝒙0 ,∴1+ 𝒙 𝟐 >0 , ∴( 𝟏+ 𝒙) 2 ≥ 𝟏 + 𝒙 𝟐 𝟐 ,即 1+ x≥1+x+ 𝒙 𝟐 𝟒 .∴x 2 ≤0. 这 与 x>0 矛盾,∴假设不成立.∴ 𝟏+ 𝒙<1+ 𝒙 𝟐
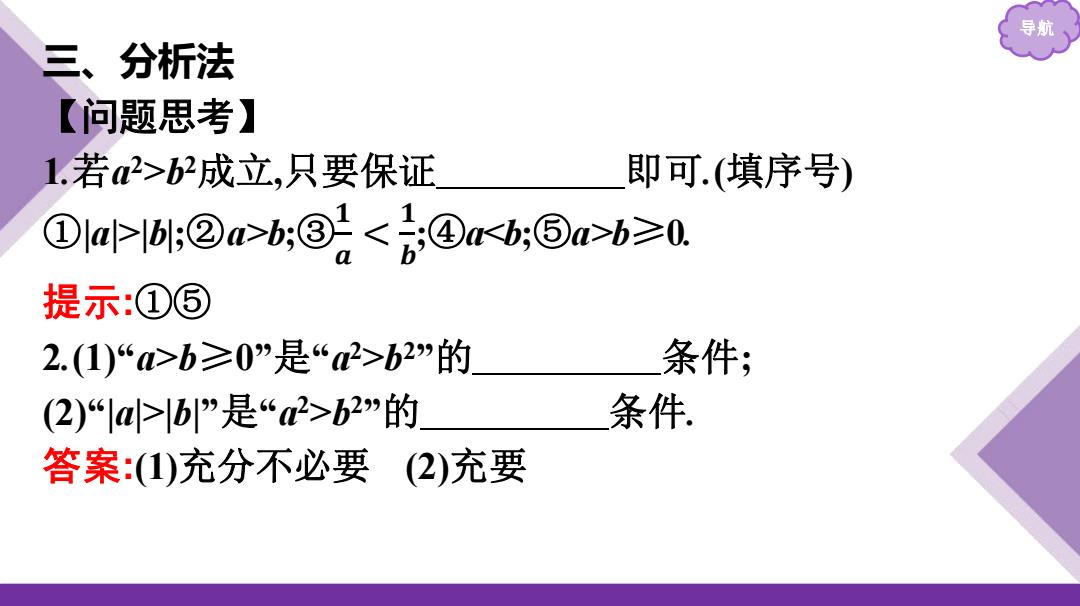
导航 三、分析法 【问题思考】 1.若2>b2成立,只要保证 即可(填序号) ①Dlal-l:②a>b:③2b≥0. 提示:①⑤ 2.(1)“>b≥0”是“a2>b2"的 条件; (2)|ab”是“a2>b2”的 条件 答案:(1)充分不必要(2)充要
导航 三、分析法 【问题思考】 1.若a 2>b2成立,只要保证 即可.(填序号) ①|a|>|b|;②a>b;③ 𝟏 𝒂 b≥0. 提示:①⑤ 2.(1)“a>b≥0”是“a 2>b2”的 条件; (2)“|a|>|b|”是“a 2>b2”的 条件. 答案:(1)充分不必要 (2)充要

3.填空:分析法中,最重要的推理形式是“ 这可以表示为,其中p是需要证明的结论,所以分析法的 实质就是不断寻找结论成立的 4.用分析法证明:v21>2-v3. 证明:要证V21>2-v3,只需证明√Z+V3>3, 只需证明(V2+V3)2>32,即5+2v69, 只需证明v62,即6>4. 因为6>4成立,所以V2-1>2-V3
导航 3.填空:分析法中,最重要的推理形式是“ 要证p,只需证明q ”, 这可以表示为 p⇐q ,其中p是需要证明的结论,所以分析法的 实质就是不断寻找结论成立的充分条件. 4.用分析法证明: 𝟐-1>2- 𝟑. 证 明:要 证 𝟐-1>2- 𝟑,只需证明 𝟐 + 𝟑>3, 只需证明( 𝟐+ 𝟑) 2 >3 2 ,即 5+2 𝟔>9 , 只需证明 𝟔>2 ,即 6>4. 因 为 6>4 成立,所以 𝟐-1>2- 𝟑

导 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“X” (1)a≥b的否定是m≤b.(×) (2)综合法是从已知条件出发开始证明的.(√) (3)分析法就是寻找使结论成立的充分条件.(√) (4)一个命题只能用一种方法证明(×)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“ ”,错误 的画“×” . (1)a≥b的否定是a≤b.( ) (2)综合法是从已知条件出发开始证明的.( ) (3)分析法就是寻找使结论成立的充分条件.( ) (4)一个命题只能用一种方法证明.( ) × ×