
全程设计 1.1.3 集合的基本运算 第1课时 交集、并集
1.1.3 集合的基本运算 第1课时 交集、并集
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1理解两个集合的交集和并集的含义 2.会求两个简单集合的交集和并集 3.能使用维恩图表达集合的关系及运算 4体会数学抽象的过程,培养直观想象、数学运算能力
导航 课标定位素养阐释 1.理解两个集合的交集和并集的含义. 2.会求两个简单集合的交集和并集. 3.能使用维恩图表达集合的关系及运算. 4.体会数学抽象的过程,培养直观想象、数学运算能力

导期 课前·基础认知 交集 【问题思考】 1.在我们班中,由所有的共青团员组成集合A,由所有的“三好 学生”组成集合B,由所有既是共青团员又是“三好学生”的同 学组成集合M,请问M与A,B有什么关系,M又可看作由什么元 素构成的? 提示:MCA,MCB.M可看作由A和B的所有公共元素构成的,集 合M叫做A与B的交集
导航 课前·基础认知 一、交集 【问题思考】 1.在我们班中,由所有的共青团员组成集合A,由所有的“三好 学生”组成集合B,由所有既是共青团员又是“三好学生”的同 学组成集合M,请问M与A,B有什么关系,M又可看作由什么元 素构成的? 提示:M⊆A,M⊆B.M可看作由A和B的所有公共元素构成的,集 合M叫做A与B的交集
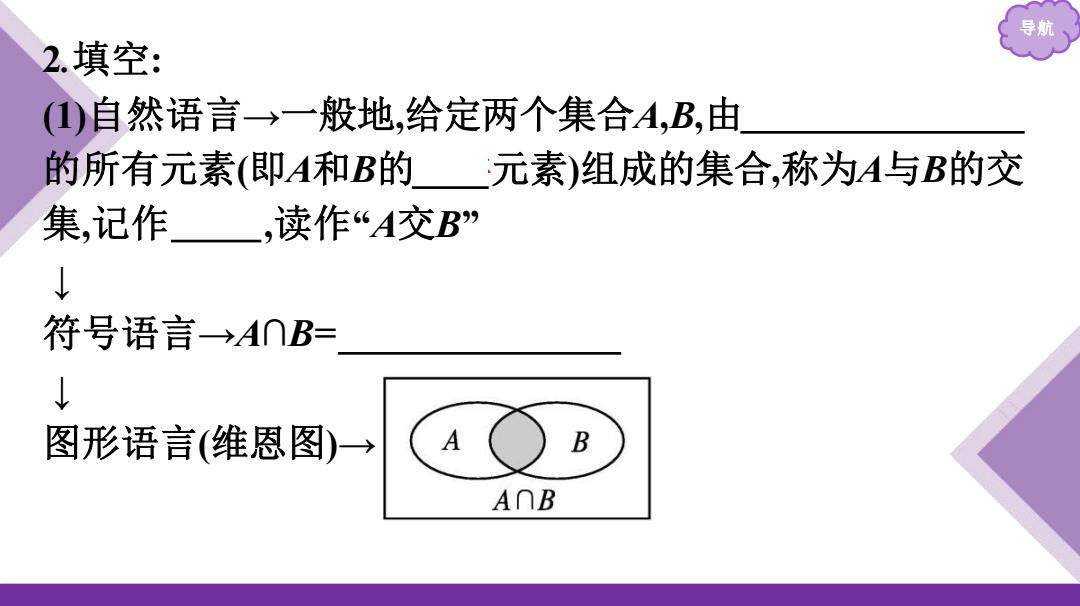
导航 2.填空: ()自然语言→一般地,给定两个集合A,B,由 的所有元素(即A和B的元素)组成的集合,称为A与B的交 集,记作,读作“A交B” ↓ 符号语言→A∩B= ↓ 图形语言(维恩图)→ A B A∩B
导航 2.填空: (1)自然语言→一般地,给定两个集合A,B,由既属于A又属于B 的所有元素(即A和B的公共元素)组成的集合,称为A与B的交 集,记作 A∩B ,读作“A交B” ↓ 符号语言→A∩B= {x|x∈A,且x∈B} ↓ 图形语言(维恩图)→

导航 (2)A∩B表示由集合A,B按照指定的法则构造出一个新 ,因 此“交”可以看成集合之间的一种运算,通常称为交集运算, 3)交集运算的性质: 对于任意两个集合A,B,都有: ①A∩B=; ②A∩A=; ③A∩o=o∩A=_; ④若A二B,则A∩B=,反之也成立
导航 (2)A∩B表示由集合A,B按照指定的法则构造出一个新集合,因 此“交”可以看成集合之间的一种运算,通常称为交集运算. (3)交集运算的性质: 对于任意两个集合A,B,都有: ①A∩B= B∩A ; ②A∩A= A ; ③A∩⌀=⌀∩A= ⌀ ; ④若A⊆B,则A∩B= A ,反之也成立

导航 3.空集⑦与自身的交集等于什么? 提示:a. 4.做一做:设集合A={1,3,5,7},B={x2≤x≤5},则A∩B=( A.{1,3} B.{3,5} C.{5,7} D.{1,7} 答案:B
导航 3.空集⌀与自身的交集等于什么? 提示:⌀. 4.做一做:设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B=( ) A.{1,3} B.{3,5} C.{5,7} D.{1,7} 答案:B

导航 二,并集 【问题思考】 1.设集合A={xx=2n,n∈Z,B={xx=2n+1,n∈Z,集合A,B与整 数集Z有何关系? 提示:A二Z,B二Z,把A,B的所有元素合在一起组成整数集Z,即 AUB-Z
导航 二、并集 【问题思考】 1.设集合A={x|x=2n,n∈Z},B={x|x=2n+1,n∈Z},集合A,B与整 数集Z有何关系? 提示:A⊆Z,B⊆Z,把A,B的所有元素合在一起组成整数集Z,即 A∪B=Z
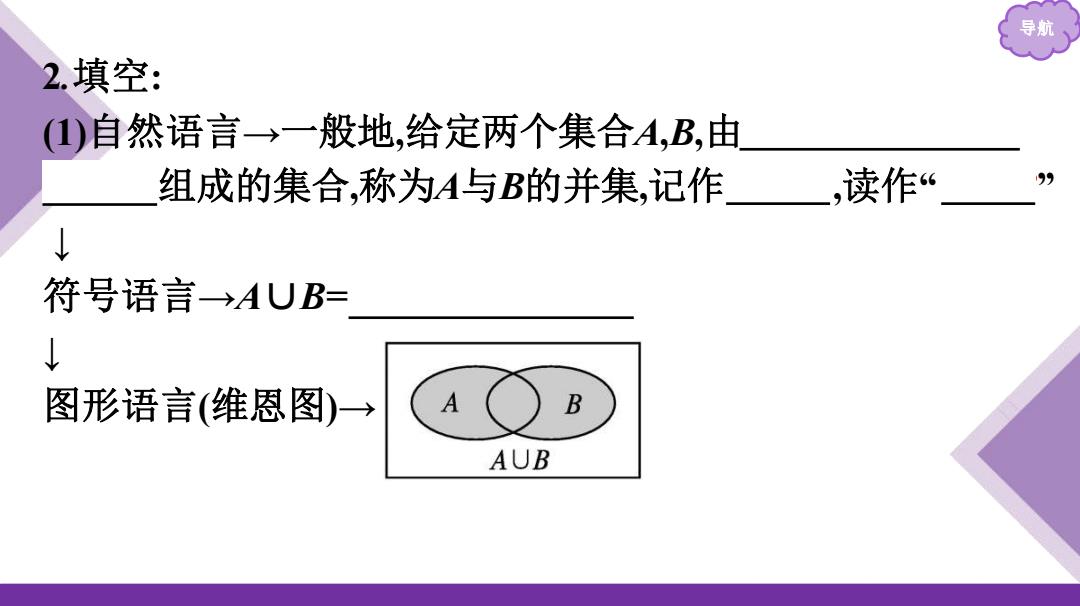
导航 2.填空: ()自然语言→一般地,给定两个集合A,B,由 组成的集合,称为A与B的并集,记作,读作“ 99 ↓ 符号语言AUB= ↓ 图形语言(维恩图)→ A B AUB
导航 2.填空: (1)自然语言→一般地,给定两个集合A,B,由这两个集合的所 有元素组成的集合,称为A与B的并集,记作 A∪B ,读作“ A并B” ↓ 符号语言→A∪B= {x|x∈A或x∈B} ↓ 图形语言(维恩图)→

(2)由集合A,B构造出AUB,通常称为运算 导期 3)并集运算的性质: 对于任意两个集合A,B,都有: ①AUB= _;②AUA=;③AUO=OUA=;④若A二B,则 AUB=,反之也成立 3.“{0,1,2U{1,3,5}={0,1,1,2,3,5}”对吗?为什么? 提示:不对.因为集合中的元素具有互异性,所以两个1归入一 个集合后只能算一个元素,即{0,1,2}U{1,3,5}={0,1,2,3,5}. 4做一做:若A=(-1,2,B={xx≥0},则AUB= 答案:(-1,十o)
导航 (2)由集合A,B构造出A∪B,通常称为并集运算. (3)并集运算的性质: 对于任意两个集合A,B,都有: ①A∪B= B∪A ;②A∪A= A ;③A∪⌀=⌀∪A= A ;④若A⊆B,则 A∪B= B ,反之也成立. 3.“{0,1,2}∪{1,3,5}={0,1,1,2,3,5}”对吗?为什么? 提示:不对.因为集合中的元素具有互异性,所以两个1归入一 个集合后只能算一个元素,即{0,1,2}∪{1,3,5}={0,1,2,3,5}. 4.做一做:若A=(-1,2],B={x|x≥0},则A∪B= . 答案:(-1,+∞)