
全程设计 4.3.2 等比数列的前n项和公式 第1课时 等比数列的前n项和公式
4.3.2 等比数列的前n项和公式 第1课时 等比数列的前n项和公式
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导期 素养·目标定位 目标素养 L.掌握等比数列的前项和公式及其应用.通过等比数列的前 n项和公式的学习,提升直观想象素养 2.会用错位相减法求数列的前项和.通过错位相减法求数列 的前n项和,提升数学运算素养
导航 目 标 素 养 1.掌握等比数列的前n项和公式及其应用.通过等比数列的前 n项和公式的学习,提升直观想象素养. 2.会用错位相减法求数列的前n项和.通过错位相减法求数列 的前n项和,提升数学运算素养. 素养·目标定位
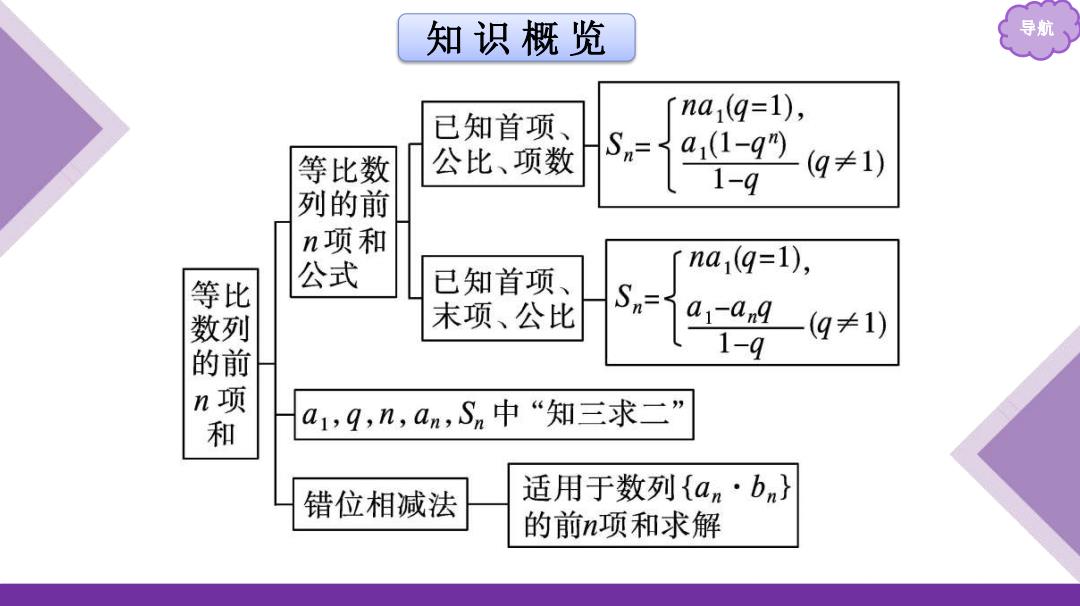
知识概览 导航 已知首项、 na1(q=1), 等比数 公比、项数 a1-g9 方 (g≠1) 列的前 n项和 等比 公式 na1(q=1), 已知首项、 数列 末项、公比 a1-an☑ 一(g≠1) 的前 s.14 n项 和 a1,q,n,am,Sn中“知三求二” 错位相减法 适用于数列{am·bn} 的前n项和求解
知 识 概 览 导航
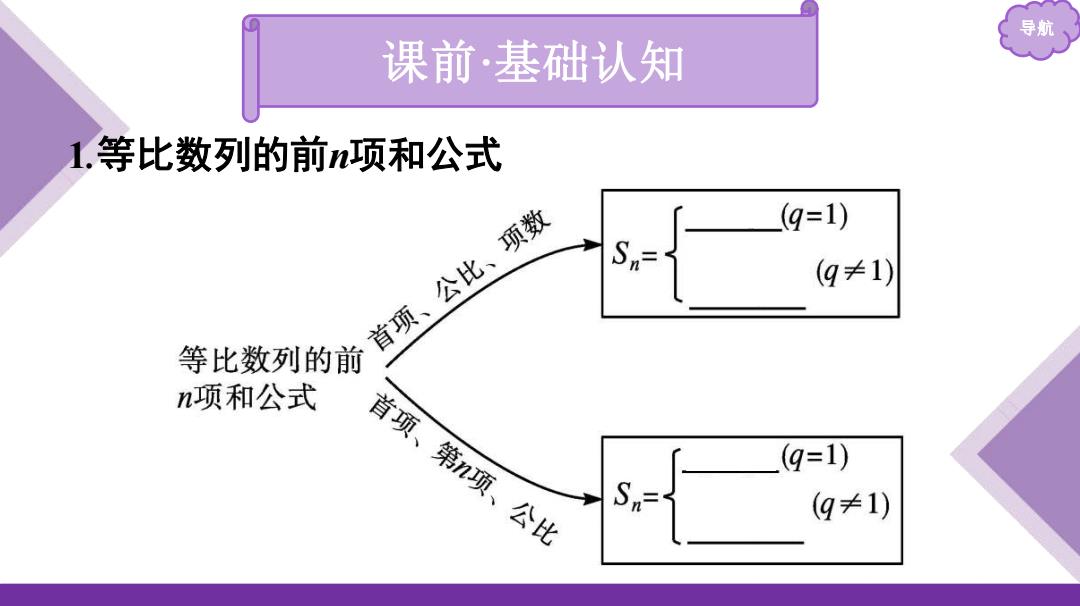
导航 课前·基础认知 1等比数列的前n项和公式 (q=1) 首项、公比、项数 S (q≠1) 等比数列的前 n项和公式 首项、第n项、公比 (q=1) S (q≠1)
导航 1 .等比数列的前 n项和公式 课前 ·基础认知

导航 微思考类比等差数列的前n项和是关于n的二次函数,如何 从函数的角度理解等比数列的前n项和Sm? 提示:可把等比数列的前n项和S,理解为关于n的指数型函数
导航 微思考 类比等差数列的前n项和是关于n的二次函数,如何 从函数的角度理解等比数列的前n项和Sn? 提示:可把等比数列的前n项和Sn理解为关于n的指数型函数

微训练1已知等比数列{am}的各项都是正数,若a1=81,=16 导航 则它的前5项和是( A.179 B.211 C.243 D.275 答案:B 解析:设等比数列{a的公比为4 16 (,且9>0, 81-16× =211. 1
微训练 导航 1已知等比数列{an }的各项都是正数,若a1 =81,a5 =16, 则它的前5项和是( ). A.179 B.211 C.243 D.275 答案:B 解析:设等比数列{an }的公比为q, ∵q 4 = 𝒂𝟓 𝒂𝟏 = 𝟏𝟔 𝟖𝟏 = 𝟐 𝟑 𝟒 ,且 q>0, ∴q= 𝟐 𝟑 ,∴S5= 𝒂𝟏-𝒂𝟓 𝒒 𝟏-𝒒 = 𝟖𝟏-𝟏𝟔× 𝟐 𝟑 𝟏- 𝟐 𝟑 =211

导航 2.41,4,n,4n,Sn中“知三求二” (1)两个公式共涉及a1,q,n,an及Sn五个基本量,它们分别表示 等比数列的首项、公比、项数、第n项和前n项和. (2)依据方程的思想,在等比数列的前项和公式中已知其中 三个量可求另外两个量,即“知三求二
导航 2.a1 ,q,n,an ,Sn中“知三求二” (1)两个公式共涉及a1 ,q,n,an及Sn五个基本量,它们分别表示 等比数列的首项、公比、项数、第n项和前n项和. (2)依据方程的思想,在等比数列的前n项和公式中已知其中 三个量可求另外两个量,即“知三求二”

导航 微训练2在等比数列{an中,若公比q二2,Ss=44,则a1的值为 () A.4 B.-4 C.2 D.-2 答案:A 解析:由Ss1-2144,得1=4 1-(-2)
导航 解析:由 S5= 𝒂𝟏[𝟏-(-𝟐) 𝟓 ] 𝟏-(-𝟐) =44,得 a1=4. 微训练2在等比数列{an }中,若公比q=-2,S5 =44,则a1的值为 ( ). A.4 B.-4 C.2 D.-2 答案:A

3.错位相减法 (1)推导等比数列前n项和的方法 一般地,等比数列{a,n的首项为a1,公比为q,则数列{a}的前n 项和可写为: S=a1ta1q+a1q2+…+a1qr-1,① 用公比乘①的两边,可得 qSn=419+a1q2+…+u1q-1+a1q",② 由①-②,得(1-q)Sm=1-414”, 整理得5
导航 3.错位相减法 (1)推导等比数列前n项和的方法 一般地,等比数列{an }的首项为a1 ,公比为q,则数列{an }的前n 项和可写为: Sn=a1+a1q+a1q 2+…+a1q n-1 ,① 用公比q乘①的两边,可得 qSn=a1q+a1q 2+…+a1q n-1+a1q n ,② 由①-②,得(1-q)Sn=a1 -a1q n , 整理得 Sn = 𝒂𝟏(𝟏-𝒒 𝒏) 𝟏-𝒒 (q≠1)