
全程设计 5.3 号数在研究函数中的应用 5.3.1 函数的单调性
5.3 导数在研究函数中的应用 5.3.1 函数的单调性
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导期 素养·目标定位 目标素养 1.结合实例,直观探索并掌握函数的单调性与导数的关系,提 升直观想象和逻辑推理核心素养 2.会求函数的单调区间,提升数学运算核心素养 3.能利用导数研究函数的单调性,并能够利用单调性求参数的 取值范围,提升逻辑推理核心素养
导航 目 标 素 养 1.结合实例,直观探索并掌握函数的单调性与导数的关系,提 升直观想象和逻辑推理核心素养. 2.会求函数的单调区间,提升数学运算核心素养. 3.能利用导数研究函数的单调性,并能够利用单调性求参数的 取值范围,提升逻辑推理核心素养. 素养·目标定位
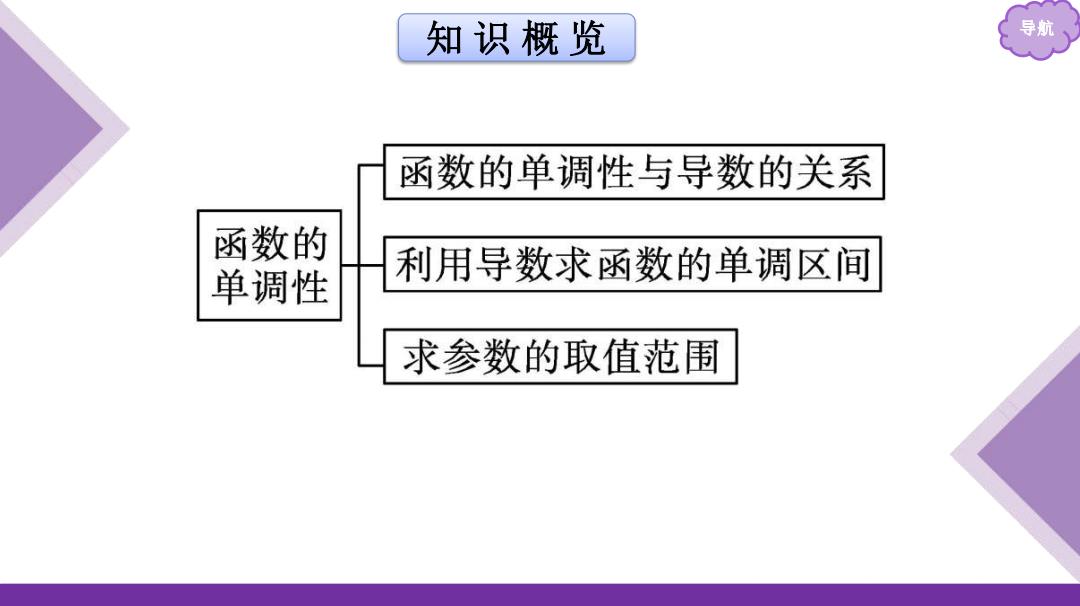
知识概览 导航 函数的单调性与导数的关系 函数的 单调性 利用导数求函数的单调区间 求参数的取值范围
知 识 概 览 导航

导期 课前·基础认知 1函数的单调性与导数的关系 般地,函数fx)的单调性与导函数f(x)的正负之间具有如 下的关系: 在某个区间(a,b)上,如果f'x)>0,那么函数y=fx)在区间(a,b) 上 4 在某个区间(a,b)上,如果fx)<0,那么函数y=fx)在区间(,b) 上
导航 1.函数的单调性与导数的关系 一般地,函数f(x)的单调性与导函数f‘(x)的正负之间具有如 下的关系: 在某个区间(a,b)上,如果f'(x)>0,那么函数y=f(x)在区间(a,b) 上 单调递增 ; 在某个区间(a,b)上,如果f'(x)<0,那么函数y=f(x)在区间(a,b) 上 单调递减 . 课前·基础认知

导航 微训练1函数fx)=x+lnx( A.在区间(0,6上单调递增 B.在区间(0,6)上单调递减 C.在区间(0,3)上单调递减,在区间(,6)上单调递增 在区间0,上单调速增在区间仁6)上单闲宽诚 答案:A
导航 微训练1函数f(x)=x+ln x( ) A.在区间(0,6)上单调递增 B.在区间(0,6)上单调递减 答案:A C.在区间 𝟎, 𝟏 𝐞 上单调递减,在区间 𝟏 𝐞 ,𝟔 上单调递增 D.在区间 𝟎, 𝟏 𝐞 上单调递增,在区间 𝟏 𝐞 ,𝟔 上单调递减

2.利用导数判断函数的单调性的步骤 一般情况下,我们可以通过如下步骤判断函数y=fx)的单调 性: 第1步,确定函数的定义域; 第2步,求出导数fx)的零点; 第3步,用fx)的零点将fx)的定义域划分为若干个区间,列表 给出fx)在各区间上的正负,由此得出函数y=fx)在定义域内 的单调性
导航 2.利用导数判断函数的单调性的步骤 一般情况下,我们可以通过如下步骤判断函数y=f(x)的单调 性: 第1步,确定函数的定义域; 第2步,求出导数f'(x)的零点; 第3步,用f'(x)的零点将f(x)的定义域划分为若干个区间,列表 给出f'(x)在各区间上的正负,由此得出函数y=f(x)在定义域内 的单调性

导航 微训练2函数fx)=3+xlnx的单调递增区间为( A(0,3) B.(e,+0) c(,+o)D.(,e) 答案:C 解析:由已知得f)=lnx+1,令f)>0, 即ln+1>0,得 故函数)的单调递增区间为(怎,+0)
导航 微训练2函数f(x)=3+xln x的单调递增区间为( ). A. 𝟎, 𝟏 𝐞 B.(e,+∞) C. 𝟏 𝐞 , + ∞ D. 𝟏 𝐞 ,𝐞 答案:C 解析:由已知得f'(x)=ln x+1,令f'(x)>0, 即 ln x+1>0,得 x> 𝟏 𝐞 . 故函数 f(x)的单调递增区间为 𝟏 𝐞 , + ∞

导航 3,函数图象的变化趋势与导数值大小的关系 般地,如果一个函数在某一范围内导数的绝对值较 那么函数在这个范围内变化得较快,这时函数的图象就比较 6G ”(向上或向下);反之,函数在这个范围内变化得较 ,函数的图象就比较
导航 3.函数图象的变化趋势与导数值大小的关系 一般地,如果一个函数在某一范围内导数的绝对值较 大 , 那么函数在这个范围内变化得较快,这时函数的图象就比较 “ 陡峭 ”(向上或向下);反之,函数在这个范围内变化得较 慢 ,函数的图象就比较“ 平缓 ”

导航 课堂·重难突破 求函数的单调区间 典例剖析 1.求下列函数的单调区间: (1)fx)=x33x+1; 2/y与x+2b>0
导航 一 求函数的单调区间 典例剖析 1.求下列函数的单调区间: (1)f(x)=x3 -3x+1; 课堂·重难突破 (2)f(x)=x+𝒃 𝒙 (b>0)