
全程设计 5.3.2 函数的极值与最大(小)值 第3课时 导数在解决实际问题中的应用
5.3.2 函数的极值与最大(小)值 第3课时 导数在解决实际问题中的应用
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导期 素养·目标定位 目标素养 1.了解导数在解决实际问题中的作用,提升数学抽象的核心素 养 2.掌握利用导数解决实际生活中简单的优化问题;学会建立 数学模型,并会求解数学模型;提升数学建模的核心素养
导航 目 标 素 养 1.了解导数在解决实际问题中的作用,提升数学抽象的核心素 养. 2.掌握利用导数解决实际生活中简单的优化问题;学会建立 数学模型,并会求解数学模型;提升数学建模的核心素养. 素养·目标定位

知识概览 导航 面积、容积的最值问题 生活中的 用料最省、成本(费用)最低问题 优化问题 利润最大、效率最高问题
知 识 概 览 导航

导航 课前·基础认知 生活中的优化问题 ()生活中经常遇到求利润最大、用料最省、效率最高等问 题,这些问题通常称为 (2)利用导数解决优化问题的实质是
导航 生活中的优化问题 (1)生活中经常遇到求利润最大、用料最省、效率最高等问 题,这些问题通常称为 优化问题 . (2)利用导数解决优化问题的实质是 求函数最值 . 课前·基础认知
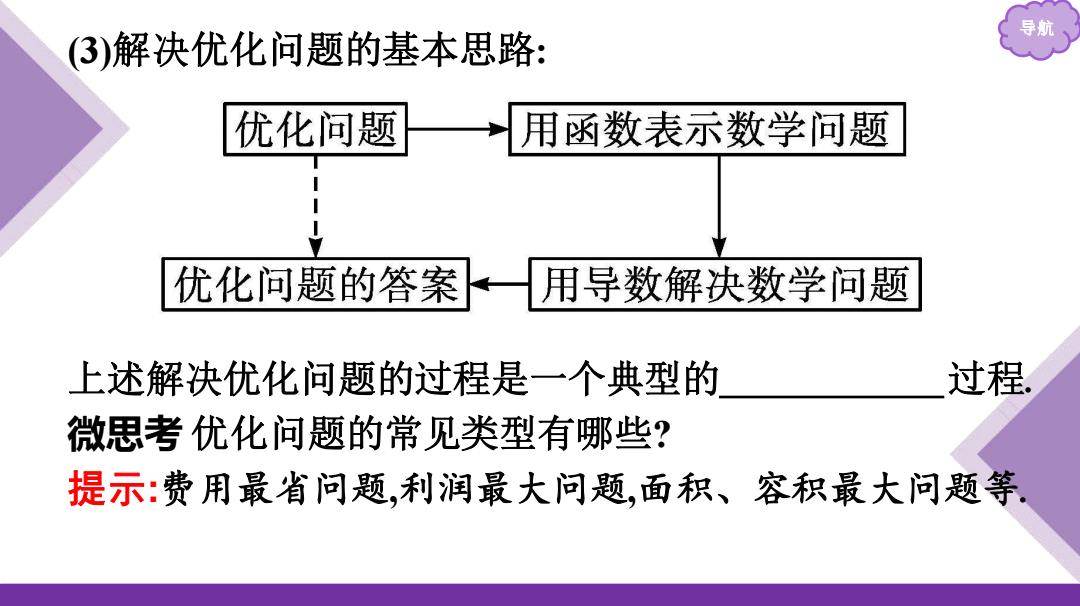
导航 (3)解决优化问题的基本思路: 优化问题 用函数表示数学问题 优化问题的答案 用导数解决数学问题 上述解决优化问题的过程是一个典型的 过程 微思考优化问题的常见类型有哪些? 提示:费用最省问题,利润最大问题,面积、容积最大问题等
导航 (3)解决优化问题的基本思路: 上述解决优化问题的过程是一个典型的 数学建模 过程. 微思考 优化问题的常见类型有哪些? 提示:费用最省问题,利润最大问题,面积、容积最大问题等

导期 课堂·重难突破 利润最大问题 典例剖析 1.某商品每件成本9元,售价30元,每星期卖出432件.如果降 低售价,销售量就会增加,且每星期多卖出的商品件数与商品 售价的降低值x(单位:元件,0≤x≤21)的平方成正比.已知当 每件商品的售价降低2元时,一星期多卖出24件 ()将该商品一个星期的销售利润表示成关于商品售价的降 低值x的函数; (2)如何定价才能使该商品一个星期的销售利润最大?
导航 一 利润最大问题 典例剖析 1.某商品每件成本9元,售价30元,每星期卖出432件.如果降 低售价,销售量就会增加,且每星期多卖出的商品件数与商品 售价的降低值x(单位:元/件,0≤x≤21)的平方成正比.已知当 每件商品的售价降低2元时,一星期多卖出24件. (1)将该商品一个星期的销售利润表示成关于商品售价的降 低值x的函数; (2)如何定价才能使该商品一个星期的销售利润最大? 课堂·重难突破

导航 解:(1)若每件商品售价降低x元, 则一个星期多卖出的商品件数为x2, 由已知条件,得k22=24,解得=6. 若记商品一个星期的销售利润为), 则有fx)=(30-x-9)(432+6x2)=-6x3+126x2-432x+9072, x∈[0,21
导航 解:(1)若每件商品售价降低x元, 则一个星期多卖出的商品件数为kx2 . 由已知条件,得k·22=24,解得k=6. 若记商品一个星期的销售利润为f(x), 则有f(x)=(30-x-9)(432+6x 2 )=-6x 3+126x 2 -432x+9 072, x∈[0,21]

(2)对(1)中函数fx)求导得f(x)=-18x2+252x432=-18(c-2)&航 12). 当x变化时,fx)fx)的变化情况如下表: (0,2) (2,12) 12 12,21) 21 f(x) + 0 x)9072 单调递减极小值 单调递增极大值单调递减0 ∴.当=12时,fx)取得极大值 .f0)=9072,12)=11664,f21)=0, ∴.当x=12时fx)取得最大值,此时30-12=18(元), 故定为18元件时,能使该商品一个星期的销售利润最大
导航 (2)对(1)中函数f(x)求导得f'(x)=-18x 2+252x-432=-18(x-2)(x- 12). 当x变化时,f'(x),f(x)的变化情况如下表: x 0 (0,2) 2 (2,12) 12 (12,21) 21 f'(x) - 0 + 0 - f(x) 9 072 单调递减 极小值 单调递增极大值 单调递减 0 ∴当x=12时,f(x)取得极大值. ∵f(0)=9 072,f(12)=11 664,f(21)=0, ∴当x=12时,f(x)取得最大值,此时30-12=18(元), 故定为18元/件时,能使该商品一个星期的销售利润最大

导航 规律总结利润最大问题是生活中常见的一类问题,一般根 据“利润=收入-成本”建立函数关系式,再利用导数求最大值 解此类问题需注意两点:(1)价格要大于或等于成本,否则就 会亏本;2)销量要大于0,否则不会获利
导航 规律总结 利润最大问题是生活中常见的一类问题,一般根 据“利润=收入-成本”建立函数关系式,再利用导数求最大值. 解此类问题需注意两点:(1)价格要大于或等于成本,否则就 会亏本;(2)销量要大于0,否则不会获利