
全程设计 1.2 常用逻辑用语 1.2.2 全称量词命题与存在量词命题 的否定
1.2 常用逻辑用语 1.2.2 全称量词命题与存在量词命题 的否定
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解命题的否定,能对一个命题进行否定 2.掌握全称量词命题、存在量词命题的否定,并理解命题与其 命题的否定之间的真假关系. 3.体会数学抽象的过程和培养逻辑推理能力
导航 课标定位素养阐释 1.了解命题的否定,能对一个命题进行否定. 2.掌握全称量词命题、存在量词命题的否定,并理解命题与其 命题的否定之间的真假关系. 3.体会数学抽象的过程和培养逻辑推理能力

导 课前·基础认知 命题的否定 【问题思考】 1.试说出“命题p:1是方程x=1的根”与“命题g:1不是方程x=1 的根”的关系,并判断p,g的真假 提示:命题是对命题p的否定,同时命题p也是对命题q的否 定,D是真命题,g是假命题 2.填空:一般地,对命题加以,就得到一个新的命题,记作 “”,读作“非p”或“ 9
导航 课前·基础认知 一、命题的否定 【问题思考】 1.试说出“命题p:1是方程|x|=1的根”与“命题q:1不是方程|x|=1 的根”的关系,并判断p,q的真假. 提示:命题q是对命题p的否定,同时命题p也是对命题q的否 定,p是真命题,q是假命题. 2.填空:一般地,对命题p加以否定,就得到一个新的命题,记作 “ ¬p ”,读作“非p”或“ p的否定 ”

导航 3.命题p与p的真假有什么关系? 提示:p与p必是一真一假 4.做一做: (1)若p:{2}是{1,2}的子集,则p是 (2)若g:52=25,则-g是 命题.(填“真”或“假) 答案:1){2}不是{1,2的子集(2)假
导航 3.命题p与¬p的真假有什么关系? 提示:p与¬p必是一真一假. 4.做一做: (1)若p:{2}是{1,2}的子集,则¬p是 . (2)若q:52=25,则¬q是 命题.(填“真”或“假”) 答案:(1){2}不是{1,2}的子集 (2)假

二、全称量词命题与存在量词命题的否定 【问题思考】 已知命题p:任何有理数都是实数;:存在点M在抛物线y=x2上, 1.指出命题p,g是存在量词命题还是全称量词命题,并判断其 真假. 提示:p是全称量词命题,是真命题;是存在量词命题,是真命 题 2.写出p和g,并判断其真假 提示:p:存在有理数不是实数,是假命题 q:任意点M都不在抛物线y=x2上,是假命题
导航 二、全称量词命题与存在量词命题的否定 【问题思考】 已知命题p:任何有理数都是实数;q:存在点M在抛物线y=x2上. 1.指出命题p,q是存在量词命题还是全称量词命题,并判断其 真假. 提示:p是全称量词命题,是真命题;q是存在量词命题,是真命 题. 2.写出¬p和¬q,并判断其真假. 提示:¬p:存在有理数不是实数,是假命题. ¬q:任意点M都不在抛物线y=x2上,是假命题
导航 3.填表: 项目 全称量词命题 存在量词命题 x∈M,q) 3x∈Mpc) 卫 3x∈M,-qx) x∈M,pc) 真假关系 命题与其命题的否定一真一假
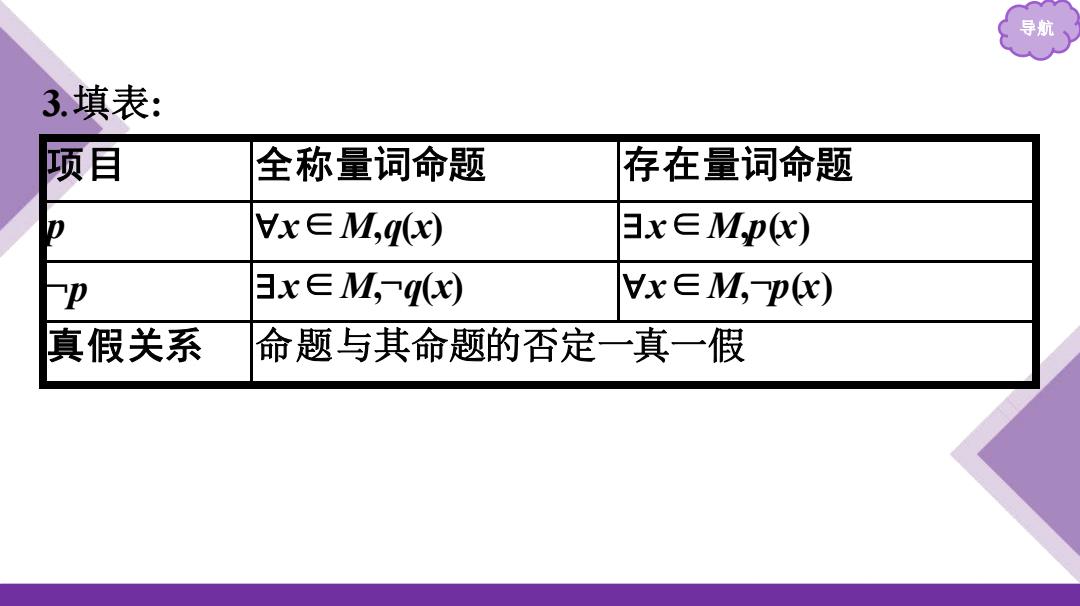
导航 3 .填表: 项 目 全称量词命题 存在量词命题 p ∀x∈M,q(x) ∃x∈M,p(x) ¬p ∃x∈M,¬q(x) ∀x∈M,¬p(x) 真假关系 命题与其命题的否定一真一假

导航 4.做一做:写出下列命题的否定,并判断所得命题的真假. (up:设A是所有角组成的集合,则v0∈Asin: (2qa∈Rua 解:(山)p:设A是所有角组成的集合,则30eA,sin62是真命题 (2)q:Va∈R吋,是假命题
导航 4.做一做:写出下列命题的否定,并判断所得命题的真假. (1)p:设 A 是所有角组成的集合,则∀θ∈A,sin θ≠ 𝟏 𝟐 ; (2)q:∃a∈R,a= 𝟏 𝒂 . 解:(1 )¬p:设 A 是所有角组成的集合,则∃θ∈A,sin θ= 𝟏 𝟐 ,是真命题. (2)¬q:∀a∈R,a≠ 𝟏 𝒂 ,是假命题

导月 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√,错误 的画“X” ()有些命题与其否定都是真命题(×) (2)任何命题都有它的否定(√) 3)全称量词命题的否定一定是存在量词命题(√) (4)无论全称量词命题还是存在量词命题,命题和其命题的否 定都是一真一假(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)有些命题与其否定都是真命题.( ) (2)任何命题都有它的否定.( ) (3)全称量词命题的否定一定是存在量词命题.( ) (4)无论全称量词命题还是存在量词命题,命题和其命题的否 定都是一真一假.( ) × √ √ √

导航 课堂·重难突破 探究一“p”形式的命题及真假判断 【例1】写出下列命题的否定,并判断其真假: (1)p:V3是有理数; (2)p:5不是75的约数; (3)p:7<8; (4)p:5+6≠11
导航 课堂·重难突破 探究一“¬p”形式的命题及真假判断 【例1】写出下列命题的否定,并判断其真假: (1)p: 是有理数; (2)p:5不是75的约数; (3)p:7<8; (4)p:5+6≠11. √𝟑