
全程设计 3.1.3 函数的奇偶性 第1课时 数的奇偶性
3.1.3 函数的奇偶性 第1课时 函数的奇偶性
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.理解函数奇偶性的定义 2.掌握函数奇偶性的判断和证明方法
导航 课标定位素养阐释 1.理解函数奇偶性的定义. 2.掌握函数奇偶性的判断和证明方法
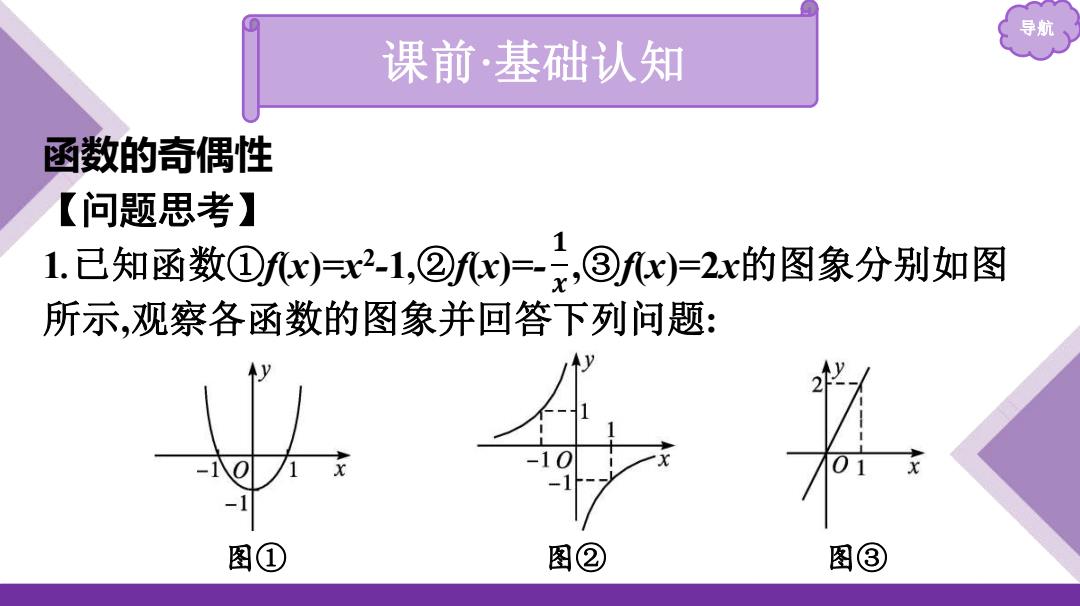
导航 课前·基础认知 函数的奇偶性 【问题思考】 1.已知函数①f)与2-1,②w)=,③e)=2x的图象分别如图 所示,观察各函数的图象并回答下列问题: 图① 图② 图③
导航 课前·基础认知 函数的奇偶性 【问题思考】 1.已知函数①f(x)=x2 -1,②f(x)=- ,③f(x)=2x的图象分别如图 所示,观察各函数的图象并回答下列问题: 𝟏 𝒙 图① 图② 图③

导航 ()各个图象有怎样的对称性? 提示:图①关于y轴对称;图②③关于坐标原点对称 (2)对于以上三个函数,分别计算f孔-x),观察对定义域内的每一 个x,x)与fx)有怎样的关系? 提示:①f-x)=x);②f-x)=fx)③f-x)=fx)
导航 (1)各个图象有怎样的对称性? 提示:图①关于y轴对称;图②③关于坐标原点对称. (2)对于以上三个函数,分别计算f(-x),观察对定义域内的每一 个x,f(-x)与f(x)有怎样的关系? 提示:①f(-x)=f(x);②f(-x)=-f(x);③f(-x)=-f(x)

导 2.填空: ()偶函数的定义:一般地,设函数y=fx)的定义域为D,如果对D 内的任意一个x,都有-x∈D,且 ,则称y=fx)为偶函数 (2)偶函数的图象特征:偶函数的图象关于对称,反之,结论 也成立 3)奇函数的定义:一般地,设函数y=fx)的定义域为D,如果对D 内的任意一个x,都有-x∈D,且 ,则称y=x)为奇函数
导航 2.填空: (1)偶函数的定义:一般地,设函数y=f(x)的定义域为D,如果对D 内的任意一个x,都有-x∈D,且 f(-x)=f(x) ,则称y=f(x)为偶函数. (2)偶函数的图象特征:偶函数的图象关于 y轴 对称,反之,结论 也成立. (3)奇函数的定义:一般地,设函数y=f(x)的定义域为D,如果对D 内的任意一个x,都有-x∈D,且 f(-x)=-f(x) ,则称y=f(x)为奇函数

导 (4)奇函数的图象特征:奇函数的图象关于对称,反之,结论 也成立 (⑤)函数的奇偶性:如果一个函数是偶函数或是奇函数,则称这 个函数具有.可以看出,当n是正整数时,函数fx)=x2n是 ,函数g(x)=x2+1是
导航 (4)奇函数的图象特征:奇函数的图象关于原点对称,反之,结论 也成立. (5)函数的奇偶性:如果一个函数是偶函数或是奇函数,则称这 个函数具有奇偶性.可以看出,当n是正整数时,函数f(x)=x2n是 偶函数,函数g(x)=x2n+1是奇函数

导航 3.做一做:(1)若定义在R上的奇函数y=fx)满足)=2,则f-) (2)函数fx)=x2-2x的图象关于 对称 解析:(1)因为y=fx)是奇函数,所以几-)二孔@)=-2. (2)因为函数fx)=x2-2x是定义在R上的偶函数,所以其图象关 于y轴对称 答案:(1)-2(2y轴
导航 3.做一做:(1)若定义在R上的奇函数y=f(x)满足f(a)=2,则f(-a) = . (2)函数f(x)=x2 -2|x|的图象关于 对称. 解析:(1)因为y=f(x)是奇函数,所以f(-a)=-f(a)=-2. (2)因为函数f(x)=x2 -2|x|是定义在R上的偶函数,所以其图象关 于y轴对称. 答案:(1)-2 (2)y轴

导 思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“X” (1)关于x轴对称的图象都是偶函数的图象(×) (2)若fx)是奇函数1)=2,则f-1)=-2.(√) (3)存在既是奇函数又是偶函数的函数,且不止一个.(√) (4)有些函数既不是奇函数也不是偶函数.(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)关于x轴对称的图象都是偶函数的图象.( ) (2)若f(x)是奇函数,f(1)=2,则f(-1)=-2.( ) (3)存在既是奇函数又是偶函数的函数,且不止一个.( ) (4)有些函数既不是奇函数也不是偶函数.( ) × √ √ √

导航 课堂·重难突破 探究一判断函数的奇偶性 【例1】判断下列函数的奇偶性: (1fx)=2-x$; (2)fx)=Vx2-1+V1-x2; an (4x) (x+1,x>0, -x+1,x<0
导航 课堂·重难突破 探究一判断函数的奇偶性 【例1】判断下列函数的奇偶性: (1)f(x)=2-|x|; (2)f(x)=√𝒙 𝟐-𝟏 + √𝟏-𝒙 𝟐; (3)f(x)= 𝒙 𝒙-𝟏 ; (4)f(x)= 𝒙 + 𝟏,𝒙 > 𝟎, -𝒙 + 𝟏,𝒙 < 𝟎