
全程设计 7.2.1 三角函数的定义
7.2.1 三角函数的定义

导航 课标定位 素养阐释 1.理解任意角的正弦、余弦、正切的定义 2.会求角的正弦、余弦、正切值 3.掌握三角函数在各象限内的符号. 4.加强数学抽象、逻辑推理、数学运算能力的培养
导航 课标定位 素养阐释 1.理解任意角的正弦、余弦、正切的定义. 2.会求角的正弦、余弦、正切值. 3.掌握三角函数在各象限内的符号. 4.加强数学抽象、逻辑推理、数学运算能力的培养
课前·基础认知 课堂·重难突破 随堂训练 思想方法
思 想 方 法 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 任意角的正弦、余弦与正切的定义 【问题思考】 1.若a∈(0,),点P3,4)在角a的终边上,由此能否求出sina cosa,tana的值?若能求出,简述过程;若不能,请说明理由, 提示:能.过点P作x轴的垂线,垂足为点M,则有OM=3, MP=4.0p=32+4-5,故sina号scos atan a专
导航 课前·基础认知 一、任意角的正弦、余弦与正切的定义 【问题思考】 1.若 α∈ 𝟎, 𝛑 𝟐 ,点 P(3,4)在角 α 的终边上,由此能否求出 sin α, cos α,tan α 的值?若能求出,简述过程;若不能,请说明理由. 提示:能.过点 P 作 x 轴的垂线,垂足为点 M,则有 OM=3, MP=4,OP= 𝟑𝟐 + 𝟒𝟐 =5,故 sin α= 𝟒 𝟓 ,cos α= 𝟑 𝟓 ,tan α= 𝟒 𝟑

导期 2.上题中,若在角a的终边上另取一点P,则sina,cosa,tana的 值有变化吗? 提示:没有变化 3.当a为任意角时,能否用上述方法求sina,cosa,tana的值? 提示:能
导航 2.上题中,若在角α的终边上另取一点P',则sin α,cos α,tan α的 值有变化吗? 提示:没有变化. 3.当α为任意角时,能否用上述方法求sin α,cos α,tan α的值? 提示:能
4.填空:()在平面直角坐标系中,设角α的终边上任意一点P航 的坐标是cy),它与原点O的距离是(=√x2+y2>0) 三角函数 定义 名称 sin a 正弦 cos a 余弦 tan a 正切 (2)对于每一个角a,都有 确定的正弦、余弦与之对应;当 0呋 时,有唯一的正切与之对应角α的正弦、余弦 与正切,都称为a的三角函数
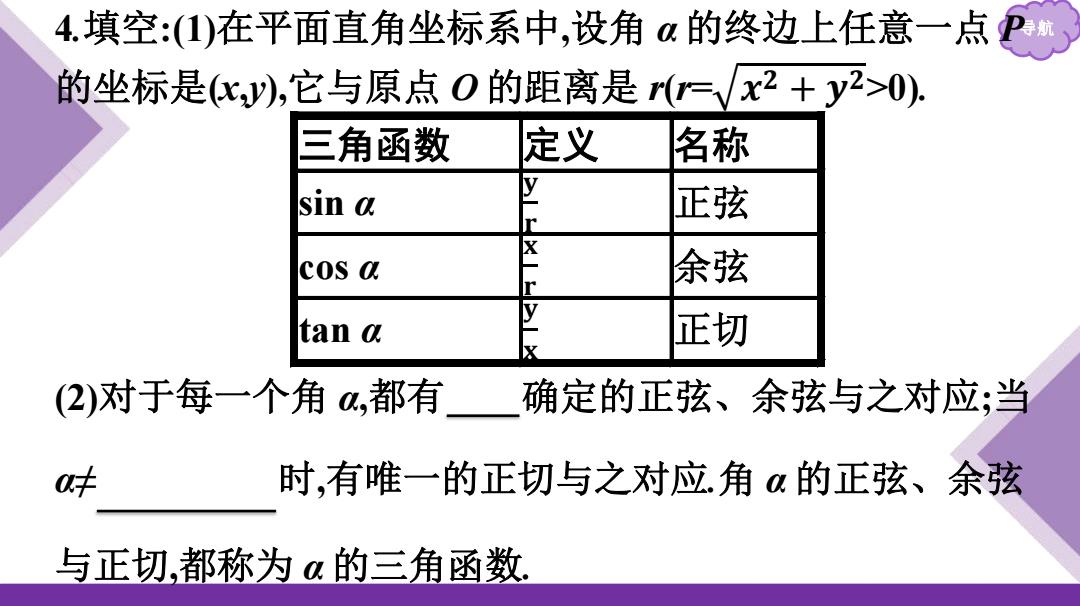
4.填空:(1)在平面直角坐标系中,设角 α 的终边上任意一点 P导航 的坐标是(x,y),它与原点 O 的距离是 r(r= 𝒙 𝟐 + 𝒚𝟐 >0). 三角函数 定义 名称 sin α 𝐲 𝐫 正弦 cos α 𝐱 𝐫 余弦 tan α 𝐲 𝐱 正切 (2)对于每一个角 α,都有唯一确定的正弦、余弦与之对应;当 α≠kπ+ 𝛑 𝟐 ,k∈Z 时,有唯一的正切与之对应.角 α 的正弦、余弦 与正切,都称为 α 的三角函数

导航 5.做一做:若点(-1,-2)在角a的终边上,则sina= cos a= ;tan a= 解析:=-1y=-2,=√x2+y2=V5, .:sin a-y_2v5 cosa÷5anar文2 答案:2 5 5 2
导航 5.做一做:若点(-1,-2)在角α的终边上,则sin α= ; cos α= ;tan α= . 解析:∵x=-1,y=-2,r= 𝒙 𝟐 + 𝒚𝟐 = 𝟓, ∴sin α= 𝒚 𝒓 =- 𝟐 𝟓 𝟓 ,cos α= 𝒙 𝒓 =- 𝟓 𝟓 ,tan α= 𝒚 𝒙 =2. 答案:- 𝟐 𝟓 𝟓 - 𝟓 𝟓 2

导航 二、正弦、 余弦与正切在各象限的符号 【问题思考】 1.不求值,你能否判断sim(-),co(-),tan( 的符号? 提示:能.3严是第三象限角,设P代,)是a终边上任一点, 则x0, 故sim(罗))=¥<0,cos())=0,tan(-)=全0
导航 二、正弦、余弦与正切在各象限的符号 【问题思考】 1.不求值,你能否判断 sin - 𝟑𝛑𝟒 ,cos - 𝟑𝛑𝟒 ,tan - 𝟑𝛑𝟒 的符号? 提示:能.-𝟑 𝛑𝟒 是第三象限角,设 P(x,y)是 α 终边上任一点, 则 x0, 故 sin - 𝟑𝛑𝟒 = 𝒚𝒓0

导 2.填空:(1)正弦、余弦、正切函数值在各象限的符号 sin a cos a tan a (2)三角函数符号的记忆口诀 三角函数在各象限的符号可简记为“全正切余”,即按象限依 次为:第一象限全为;第二象限正弦为正;第三象限正切为正; 第四象限余弦为正
导航 2.填空:(1)正弦、余弦、正切函数值在各象限的符号 (2)三角函数符号的记忆口诀 三角函数在各象限的符号可简记为“全正切余”,即按象限依 次为:第一象限全为正;第二象限正弦为正;第三象限正切为正; 第四象限余弦为正
导航、 3) 角a sin a cos a tan a a=2kπ(k∈Z)) 0 1 0 =2km+k∈☑ 0 a=2km+π(k∈Z☑) 0 0 a=-2km+3k∈Z☑ 0 不存在 3.做一做:若cosa>0,tana<0,则角a是第 象限角 答案:四
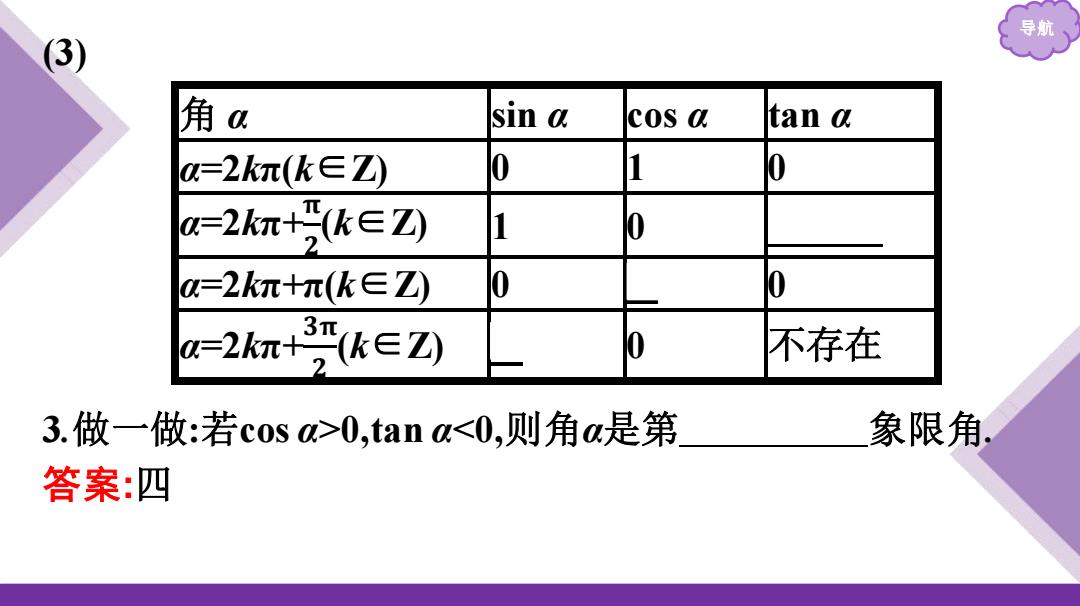
导航 (3) 角 α sin α cos α tan α α=2kπ(k∈Z) 0 1 0 α=2kπ+ 𝛑 𝟐 (k∈Z) 1 0 不存在 α=2kπ+π(k∈Z) 0 -1 0 α=2kπ+ 𝟑𝛑 𝟐 (k∈Z) -1 0 不存在 3.做一做:若cos α>0,tan α<0,则角α是第 象限角. 答案:四