
全程设计 8.2.1 两确和与差的余弦
8.2.1 两角和与差的余弦

导 课标定位 素养阐释 1.经历用向量的数量积推导出两角差的余弦公式的过程,进 一步体会向量方法的作用. 2.能利用两角差的余弦公式推导出两角和的余弦公式 3.能利用两角和与差的余弦公式化简、求值 4.加强逻辑推理和数学运算能力的培养
导航 课标定位 素养阐释 1. 经历用向量的数量积推导出两角差的余弦公式的过程,进 一步体会向量方法的作用. 2.能利用两角差的余弦公式推导出两角和的余弦公式. 3.能利用两角和与差的余弦公式化简、求值. 4.加强逻辑推理和数学运算能力的培养
课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 两角差的余弦公式 【问题思考】 1.我们知道60°=90°-30°,那么c0s60°与0°角,30°角的正弦值、 余弦值是否有关系?是怎样的关系? 提示:有,c0s60°=c0s(90°-30) =c0s90°c0s30°+sin90°sin30°=. 2 2.填空:对任意a与B,都有c0s(a-)= ,这就 是两角差的余弦公式,简记为Caf
导航 课前·基础认知 一、两角差的余弦公式 【问题思考】 1.我们知道60° =90°-30° ,那么cos 60°与90°角,30°角的正弦值、 余弦值是否有关系?是怎样的关系? 提示:有,cos 60° =cos(90°-30°) =cos 90° cos 30°+sin 90°sin 30° = . 𝟏 𝟐 2.填空:对任意α与β,都有cos(α-β)= cos αcos β+sin αsin β ,这就 是两角差的余弦公式,简记为Cα-β
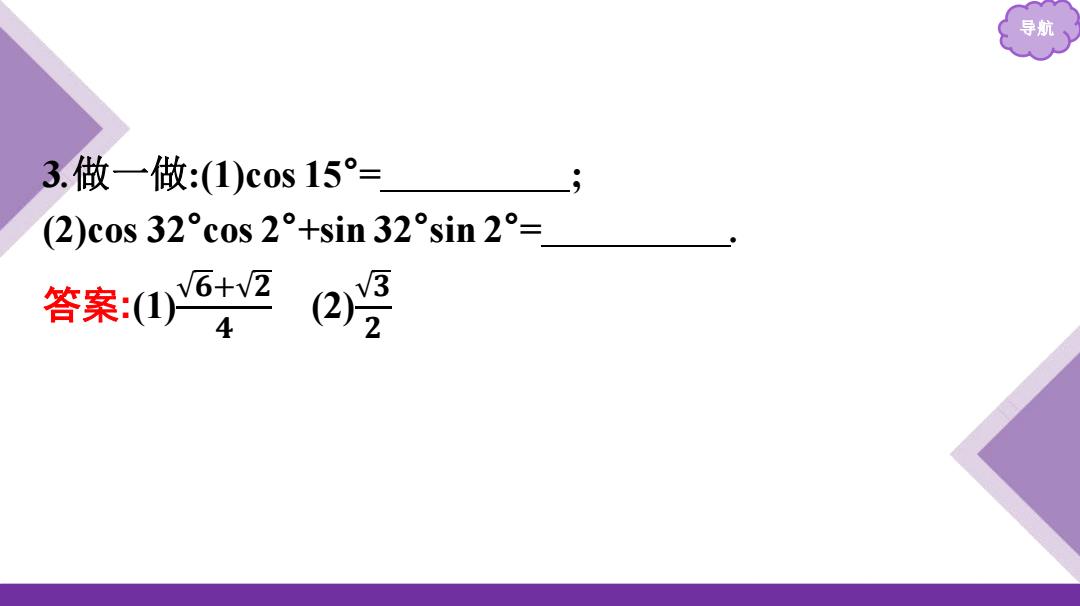
导航 3.做一做:(1)cos15°= ● (2)c0s32°c0s2°+sin32°sin2°= 答案:62(a月
导航 3.做一做:(1)cos 15° = ; (2)cos 32°cos 2°+sin 32°sin 2° = . 答案:(1) 𝟔+ 𝟐 𝟒 (2) 𝟑 𝟐

二、两角和的余弦公式 导航 【问题思考】 1.你能计算cos75°的值吗? 提示:c0s75°=c0s45°-(-30)] =cos45°c0s(-30)+sin45°sin(-30) =cos45°.cos30°-sin45°sin30° √6-VZ 4 2.填空:两角和的余弦公式Ca+即c0s(a+)=
导航 二、两角和的余弦公式 【问题思考】 1.你能计算cos 75°的值吗? 提示:cos 75° =cos[45°-(-30°)] =cos 45°cos(-30°)+sin 45°sin(-30°) =cos 45°·cos 30°-sin 45°sin 30° = 𝟔- 𝟐 𝟒 . 2.填空:两角和的余弦公式Cα+β ,即cos(α+β)= cos αcos β-sin αsin β
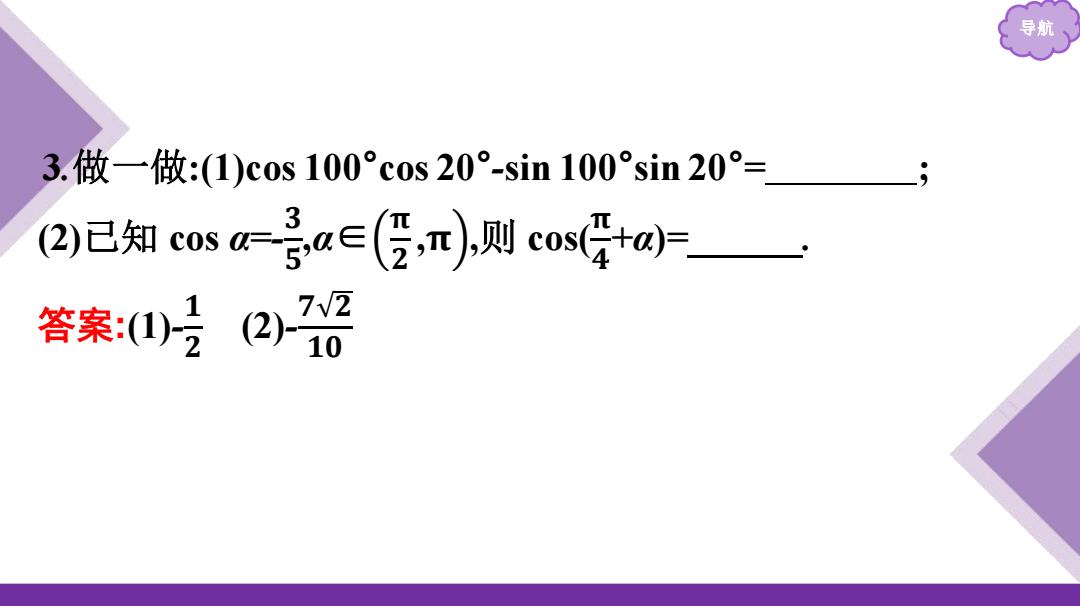
导航 3.做一做:(1)c0s100°c0s20°-sin100°sin20°=; (2)已知cosa-a∈(,n则cos+a片 答案:(山片27晋
导航 3.做一做:(1)cos 100°cos 20°-sin 100°sin 20° = ; (2)已知 cos α=- 𝟑 𝟓 ,α∈ 𝛑 𝟐 ,𝛑 ,则 cos( 𝛑 𝟒 +α)= . 答案:(1)- 𝟏 𝟐 (2)- 𝟕 𝟐 𝟏𝟎

思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X”. (1)当a,B∈R时,cos(a-)=cos acos B-sin asin B.( (2)当a,B∈R时,cos(a-B)=cos acos B+sin asin B.( 3)存在实数a,P,使cos(a+)=cos-c0sB成立.( (4)cos(a+)cos(-a)-sina+)sin(a)-cos 2a(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“ ”,错 误的画“×” . (1)当α,β∈R时,cos(α-β)=cos αcos β-sin αsin β.( × ) (2)当α,β∈R时,cos(α-β)=cos αcos β+sin αsin β.( √ ) (3)存在实数α,β,使cos(α+β)=cos α-cos β成立.( √ ) (4)cos 𝜶 + 𝛑 𝟒 cos 𝛑 𝟒 -𝜶 -sin 𝜶 + 𝛑 𝟒 sin( 𝛑 𝟒 -α)=cos 2α.( × )

导航 课堂·重难突破 探究一给角求值问题 【例1】(1)cos345°的值等于( V②-6 B.6v2 4 C②46 D.- 2+V6 4 4 解析:c0s345°=c0s15°=c0s(60°-45 =c0s60°c0s45°+sin60°sin45° -②+V6 4 答案:C
导航 课堂·重难突破 探究一 给角求值问题 【例1】(1)cos 345°的值等于( ) A. 𝟐- 𝟔 𝟒 B. 𝟔- 𝟐 𝟒 C. 𝟐+ 𝟔 𝟒 D.- 𝟐+ 𝟔 𝟒 解析:cos 345° =cos 15° =cos(60°-45°) =cos 60° cos 45°+sin 60°sin 45° = 𝟐+ 𝟔 𝟒 . 答案:C

导航、 (2)化简下列各式: ①c0s(0+21)c0s(0-24)+sin(0+21)sin(0-24); ②-sin167°sin223°+sin257°sin313. 分析:灵活运用两角和与差的余弦公式求值
导航 (2)化简下列各式: ①cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°); ②-sin 167°sin 223°+sin 257°sin 313° . 分析:灵活运用两角和与差的余弦公式求值