
全程设计 第四章 指数函数、对数函数与幂函数 4.2.3 对数函数的性质与图象 第1课时 对数函数的性质与图象
第四章 指数函数、对数函数与幂函数 4.2.3 对数函数的性质与图象 第1课时 对数函数的性质与图象

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 对数函数的概念 【问题思考】 1.将指数式=x(>0,且1)化成对数式得y=logx,请问: y=logx(a>0,且呋1)是函数吗?若是,指明其定义域;若不是,请 说明理由. 提示:是,定义域为(0,十o)
导航 课前·基础认知 一、对数函数的概念 【问题思考】 1.将指数式a y=x(a>0,且a≠1)化成对数式得y=logax,请问: y=logax(a>0,且a≠1)是函数吗?若是,指明其定义域;若不是,请 说明理由. 提示:是,定义域为(0,+∞)

导月 2.填空:一般地,函数 称为对数函数,其中是常数,>0, 且呋1. 特别地,以10为底的对数函数 叫做常用对数函数,以e为 底的对数函数 叫做自然对数函数 3.怎样判断一个函数是对数函数? 提示:(1)形如y=l0gx;(2)底数m满足心0,且1;3)真数为x,而 不是x的函数;(4)定义域为(0,+∞)
导航 2.填空:一般地,函数y=logax 称为对数函数,其中a是常数,a>0, 且a≠1. 特别地,以10为底的对数函数y=lg x 叫做常用对数函数,以e为 底的对数函数 y=ln x 叫做自然对数函数. 3.怎样判断一个函数是对数函数? 提示:(1)形如y=logax;(2)底数a满足a>0,且a≠1;(3)真数为x,而 不是x的函数;(4)定义域为(0,+∞)

二、对数函数的图象、性质 【问题思考】 L对数函数y=logx(>0,呋1)的定义域是什么?它可能是奇函 数或偶函数吗? 提示:x∈(0,+o0),不能是奇函数,也不能是偶函数, 2.如何作函数y=log2x的图象? 提示:描点法 3.函数Jy=logx与ylog1x(>0,且1)的图象有何关系? 提示:关于x轴对称
二、对数函数的图象、性质 导航 【问题思考】 1.对数函数y=logax(a>0,a≠1)的定义域是什么?它可能是奇函 数或偶函数吗? 提示:x∈(0,+∞),不能是奇函数,也不能是偶函数. 2.如何作函数y=log2x的图象? 提示:描点法. 3.函数 y=logax 与 y=lo𝐠𝟏 𝒂 x(a>0,且 a≠1)的图象有何关系? 提示:关于x轴对称
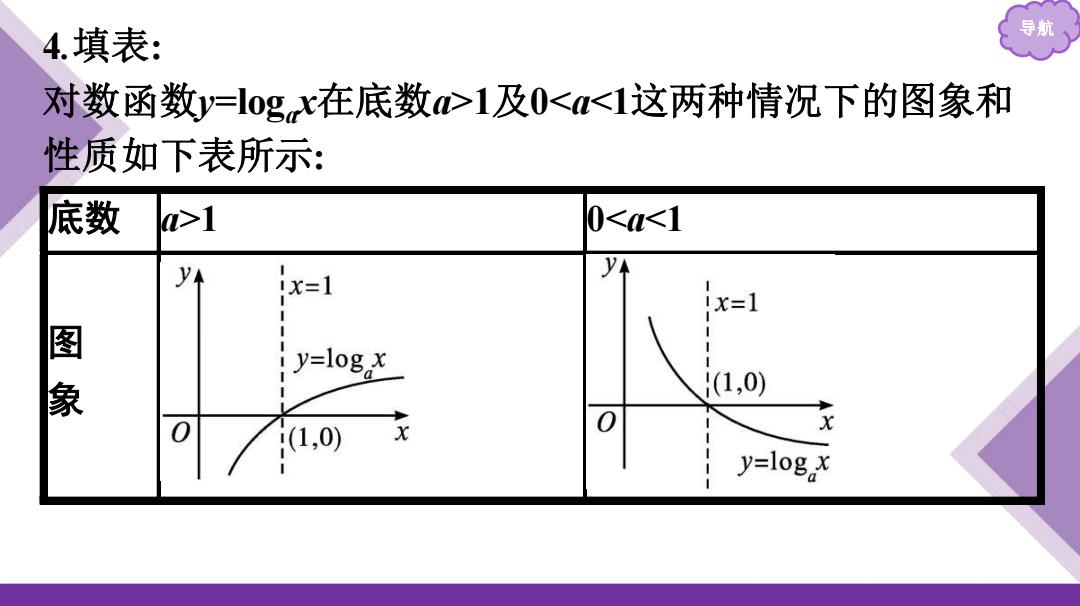
4填表: 导航 对数函数y=logx在底数心1及01 0<a<1 y y ix=1 1x=1 图象 y=logx 1,0) 0 11,0) 0 y=log。x
导航 4.填表: 对数函数y=logax在底数a>1及01 0<a<1 图 象

导航、 底数 >1 0<<1 定义域: 性质 值域:_ 过定点,即=1时y0 在区间(0,+o)内是 在区间(0,+o)内是
导航 底数 a>1 0<a<1 性 质 定义域:(0,+∞) 值域:R 过定点(1,0),即 x=1 时,y=0 在区间(0,+∞)内是增函数 在区间(0,+∞)内是减函数

导航 5.做一做:(1)函数y=log(1-2x)(a>0,呋1)的定义域 是 2若函数)ga+2是区间0,+∞)内的减函数,则实数a的取 值范围是 答案:(1)(-∞ )(2)06,-3)
导航 5.做一做:(1)函数y=loga (1-2x)(a>0,a≠1)的定义域 是 ; (2)若函数 y=lo𝐠 𝟏 𝟑 𝒂+𝟐 x 是区间(0,+∞)内的减函数,则实数 a 的取 值范围是 . 答案:(1) -∞, 𝟏 𝟐 (2)(-6,-3)

导航 课堂·重难突破 探究一求与对数函数有关的函数定义域 【例1】求函数f)=√1g(2-x)的定义域. 解:由题意得 2,0即 2-x之1也即x≤1. 2-x>0, 故函数x)=√g(2-x)的定义域为{xk≤1}
导航 课堂·重难突破 探究一 求与对数函数有关的函数定义域 【例 1】 求函数 f(x)= 𝐥𝐠(𝟐-𝒙)的定义域. 解:由题意得 𝐥𝐠(𝟐-𝒙) ≥ 𝟎, 𝟐-𝒙 > 𝟎, 即 𝟐-𝒙 ≥ 𝟏, 𝟐-𝒙 > 𝟎, 也即 x≤1. 故函数 f(x)= 𝐥𝐠(𝟐-𝒙)的定义域为{x|x≤1}

导航 延伸探究 本例变为:(1)求y=1og1(2-x)的定义域; 2 ②求)厂品的定义域
导航 本例变为:(1)求 y= 𝐥𝐨𝐠𝟏 𝟐 (𝟐-𝒙)的定义域; (2)求 y= 𝟏 𝐥𝐠(𝟐-𝒙) 的定义域