
全程设计 第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.1向量的概念
第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.1 向量的概念

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导 课前·基础认知 位移与向量 【问题思考】 1.在物理中,我们学习过力,那么两个力相等的充要条件是什 么? 提示:大小相等,且方向相同. 2.在物理中,如何表示一个力? 提示:用有向线段表示,线段的长度表示力的大小,有向线段的 方向表示力的方向
导航 课前·基础认知 一、位移与向量 【问题思考】 1.在物理中,我们学习过力,那么两个力相等的充要条件是什 么? 提示:大小相等,且方向相同. 2.在物理中,如何表示一个力? 提示:用有向线段表示,线段的长度表示力的大小,有向线段的 方向表示力的方向

3.填表:向量的概念及表示 导航 既有 又有 的量称为向量(也称为矢量); 樱 向量的 称为向量的模(或长度); 只有大小的量称为 用 表示向量,有向线段的 表示向量的大 果 小,有向线段 所指的方向表示向量的方向.以A为 始点,B为终点的有向线段表示的向量,可以用符号简记 为AB,此时向量的模用 表示 在印刷时,通常用加粗的斜体小写字母a,b,c等表示; 代数 表示 在书写时,用带箭头的小写字母如 等表示 向量a的模也用al或d来表示
导航 3 .填表 :向量的概念及表示. 概 念 既有大小又有方向的量称为向量(也称为矢量); 向量的大小称为向量的模(或长度); 只有大小的量称为标量 向量 表示 用有向线段表示向量,有向线段的长度表示向量的大 小,有向线段箭头所指的方向表示向量的方向.以 A 为 始点,B 为终点的有向线段表示的向量,可以用符号简记 为𝐀 𝐁 ,此时向量的模用|𝐀 𝐁 |表示 代数 表示 在印刷时,通常用加粗的斜体小写字母 a,b,c 等表示; 在书写时,用带箭头的小写字母如 𝒂 , 𝒃 , 𝒄 等表示. 向量 a 的模也用|a|或|𝒂 |来表示
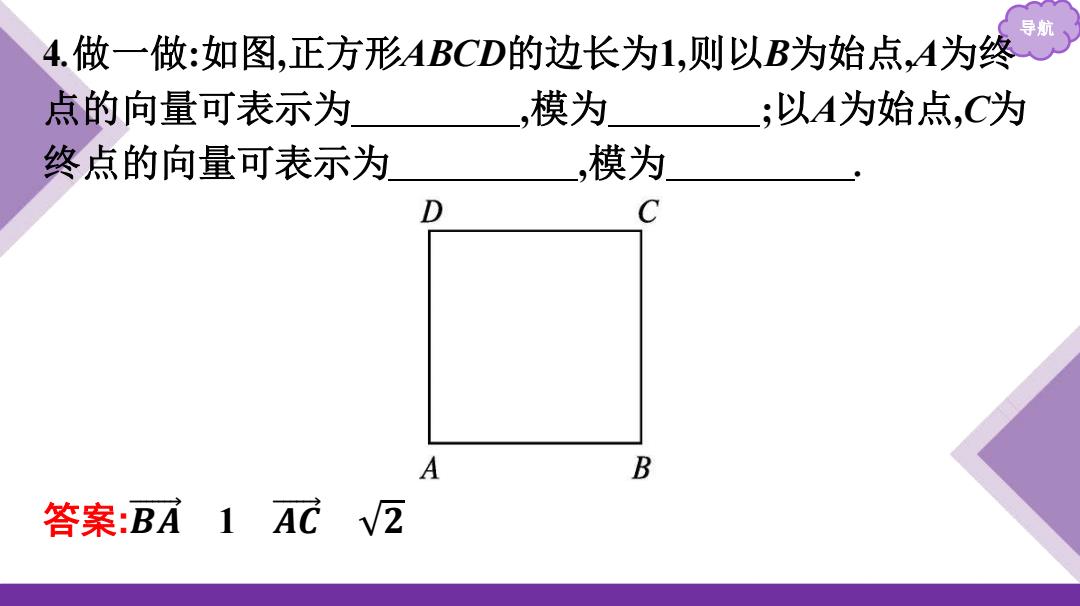
导航 4.做一做:如图,正方形ABCD的边长为1,则以B为始点,A为终 点的向量可表示为 ,模为 ;以A为始点,C为 终点的向量可表示为 ,模为 C A B 答案:BA1AC√2
导航 4.做一做:如图,正方形ABCD的边长为1,则以B为始点,A为终 点的向量可表示为 ,模为 ;以A为始点,C为 终点的向量可表示为 ,模为 . 答案:𝑩 𝑨 1 𝑨 𝑪 𝟐

导航 二、与向量有关的概念 【问题思考】 1.将有向线段AB向左平移一段距离,得到有向线段CD,AB与CD 是什么关系? 提示:向量AB与CD相等
导航 二、与向量有关的概念 【问题思考】 1.将有向线段𝑨 𝑩 向左平移一段距离,得到有向线段𝑪 𝑫 ,𝑨 𝑩 与𝑪 𝑫 是什么关系? 提示:向量𝑨 𝑩 与𝑪 𝑫 相等
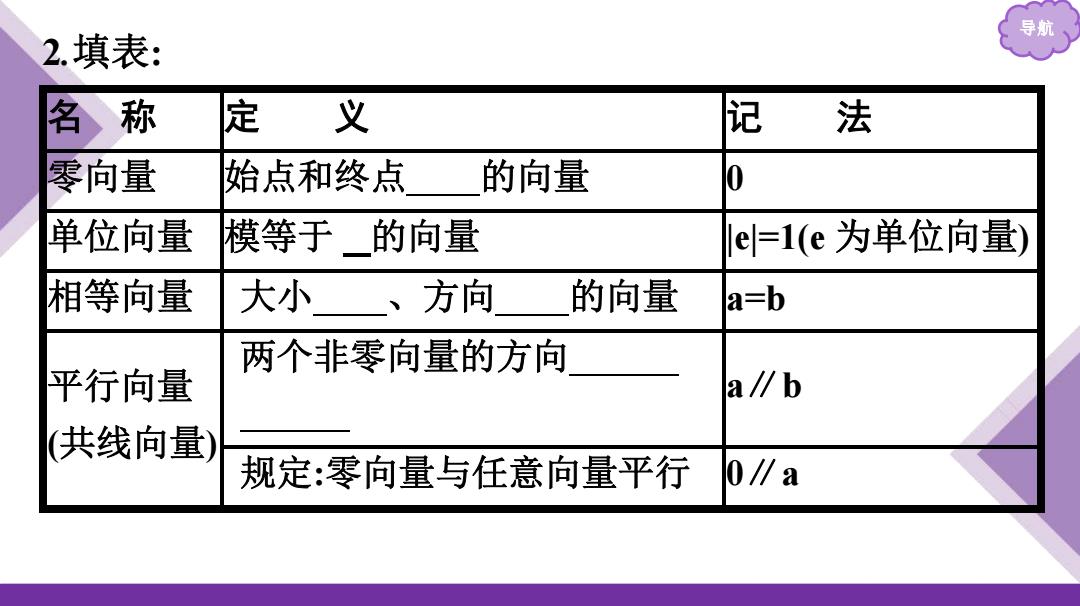
导航 2.填表: 名称 定义 记法 零向量 始点和终点 的向量 0 单位向量 模等于的向量 le=l(e为单位向量) 相等向量 大小、方向 的向量 a=b 两个非零向量的方向 平行向量 a∥b 共线向量) 规定:零向量与任意向量平行 0∥a
导航 2 .填表: 名 称 定 义 记 法 零向量 始点和终点相同的向量 0 单位向量 模等于 1 的向量 |e|=1(e 为单位向量) 相等向量 大小相等、方向相同的向量 a = b 平行向量 (共线向量) 两个非零向量的方向相同或 者相反 a ∥ b 规定:零向量与任意向量平行 0 ∥ a
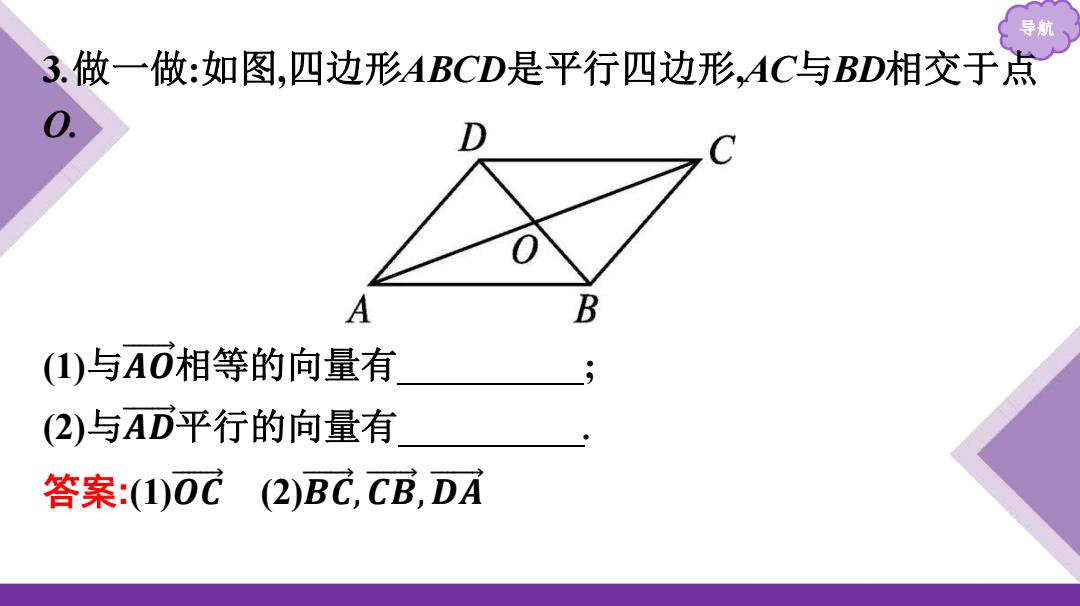
导航 3.做一做:如图,四边形ABCD是平行四边形,AC与BD相交于点 A B (1)与AO相等的向量有 (2)与AD平行的向量有 答案:1)0C(2)BC,CB,DA
导航 3.做一做:如图,四边形ABCD是平行四边形,AC与BD相交于点 O. (1)与𝑨 𝑶 相等的向量有 ; (2)与𝑨 𝑫 平行的向量有 . 答案:(1)𝑶 𝑪 (2)𝑩 𝑪 ,𝑪 𝑩 , 𝑫 𝑨

导航 课堂·重难突破 探究一向量的有关概念的理解 【例1】判断下列命题是否正确,请说明理由: (1)若向量a与b同向,且a>bl,则a>b; (2)若向量1a=b,则a与b的长度相等,且方向相同或相反; (3)对于任意向量la=b,若a与b的方向相同,则a=b; (4)由于0的方向不确定,因此0不与任意向量平行; (⑤)若向量a与向量b平行,则向量a与b的方向相同或相反
导航 课堂·重难突破 探究一 向量的有关概念的理解 【例1】判断下列命题是否正确,请说明理由: (1)若向量a与b同向,且|a|>|b|,则a>b; (2)若向量|a|=|b|,则a与b的长度相等,且方向相同或相反; (3)对于任意向量|a|=|b|,若a与b的方向相同,则a=b; (4)由于0的方向不确定,因此0不与任意向量平行; (5)若向量a与向量b平行,则向量a与b的方向相同或相反

分析:决定向量的有大小和方向两个要素,注意理解向量的有 关概念. 解:)不正确.因为向量由两个因素来确定,即大小和方向,所以 两个向量不能比较大小 (2)不正确.由=b只能判断两个向量的长度相等,不能确定它 们的方向关系. (3)正确.因为a=b,且a与b同向,由两向量相等的条件,可得a=b. (4)不正确.依据规定:0与任意向量平行 (⑤)不正确.因为向量a与向量b若有一个是零向量,则其方向不 定
分析 导航 :决定向量的有大小和方向两个要素,注意理解向量的有 关概念. 解:(1)不正确.因为向量由两个因素来确定,即大小和方向,所以 两个向量不能比较大小. (2)不正确.由|a|=|b|只能判断两个向量的长度相等,不能确定它 们的方向关系. (3)正确.因为|a|=|b|,且a与b同向,由两向量相等的条件,可得a=b. (4)不正确.依据规定:0与任意向量平行. (5)不正确.因为向量a与向量b若有一个是零向量,则其方向不 定