
全程设计 第九章 解三角形 9.3 数学探究活动 得到不可达两点之 间的距离
第九章 解三角形 9.3 数学探究活动 得到不可达两点之 间的距离

导航、 课标定位素养阐释 1.了解数学建模的意义 2.能够建立数学模型求解“得到不可达两点之间的距离”问题 3.提升数学运算、逻辑推理和直观想象的数学素养
导航 课标定位素养阐释 1.了解数学建模的意义. 2.能够建立数学模型求解“得到不可达两点之间的距离”问题. 3.提升数学运算、逻辑推理和直观想象的数学素养

导航、 一、活动背景介绍 借助米尺与测量角度的仪器,得到不可达两点之间的距离
导航 一、活动背景介绍 借助米尺与测量角度的仪器,得到不可达两点之间的距离
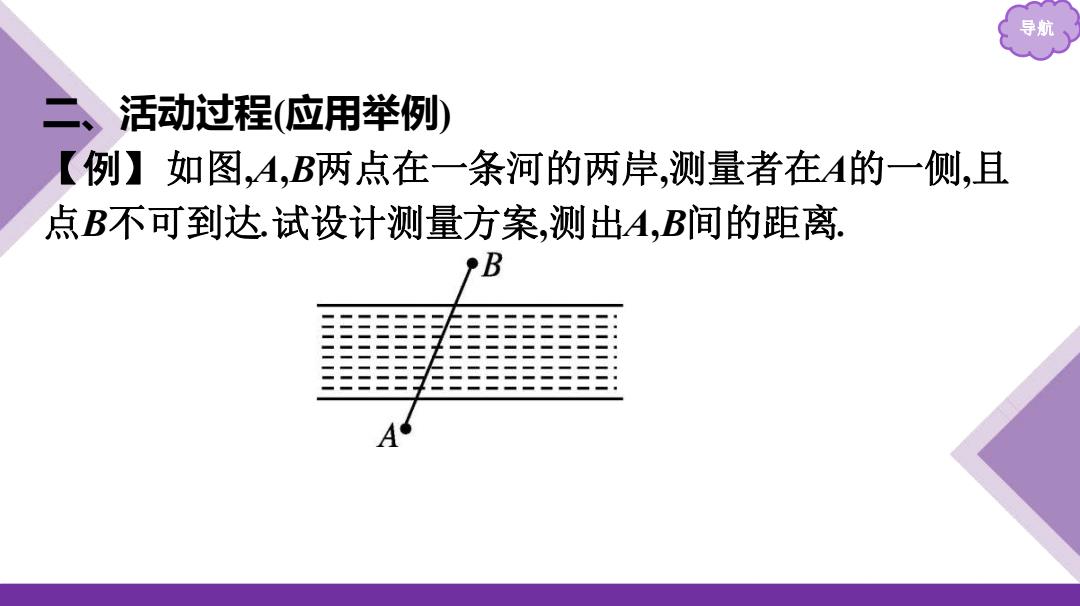
导航 二、活动过程(应用举例 【例】如图,A,B两点在一条河的两岸,测量者在A的一侧,且 点B不可到达试设计测量方案,测出A,B间的距离 A
导航 二、活动过程(应用举例) 【例】如图,A,B两点在一条河的两岸,测量者在A的一侧,且 点B不可到达.试设计测量方案,测出A,B间的距离

分析:本例中A,B两点能看到,但,点B不能到达可将AB看作三 角形的一条边的长,通过构造三角形、解三角形求得AB的长. 方法设计:在A所在的岸边选定一点C,测出A,C间的距离(设为 m, 测出∠ACB,∠CAB的大小(设∠ACB=,∠CAB=) 则在△ABC中,∠ABC=180°-(a+), 由正弦定理,得 AB AC sin∠ABC 所以AB=AC.sin.∠ACB msina sin∠ABC sin(a+β)i
导航 分析:本例中A,B两点能看到,但点B不能到达.可将AB看作三 角形的一条边的长,通过构造三角形、解三角形求得AB的长. 方法设计:在A所在的岸边选定一点C,测出A,C间的距离(设为 m), 测出∠ACB,∠CAB的大小(设∠ACB=α,∠CAB=β). 则在△ABC中,∠ABC=180°-(α+β), 由正弦定理,得 𝑨𝑩 𝐬𝐢𝐧∠𝑨𝑪𝑩 = 𝑨𝑪 𝐬𝐢𝐧∠𝑨𝑩𝑪 , 所以 AB=𝑨𝑪·𝐬𝐢𝐧∠𝑨𝑪𝑩 𝐬𝐢𝐧∠𝑨𝑩𝑪 = 𝒎𝐬𝐢𝐧𝜶 𝐬𝐢𝐧(𝜶+𝜷)

导航 反思感悟 求不可达两点之间的距离关键是构造三角形(一个或几个),然 后根据需要测出有关量,最后借助于正弦定理、余弦定理求 出这两点之间的距离
导航 求不可达两点之间的距离关键是构造三角形(一个或几个),然 后根据需要测出有关量,最后借助于正弦定理、余弦定理求 出这两点之间的距离

导航 【变式训练】设计一个方案,测出山AB的高.(山顶A可视,山 底B不可视,A,B均不能到达)
导航 【变式训练】设计一个方案,测出山AB的高.(山顶A可视,山 底B不可视,A,B均不能到达)
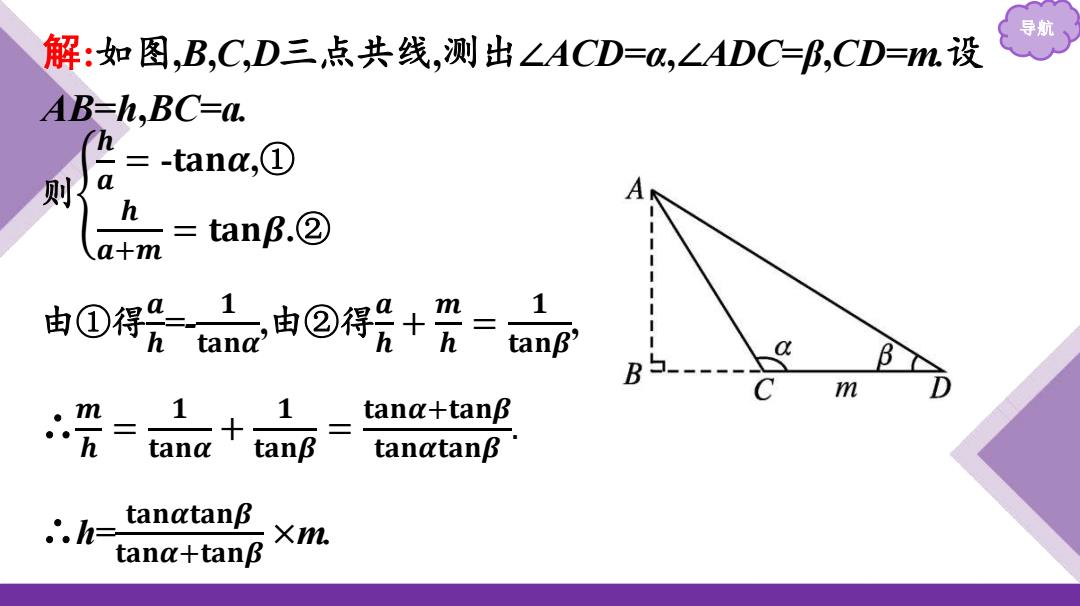
解:如图,B,C,D三点共线,测出∠ACD=a,∠ADC=B,CD=m设 AB=h,BC=a. h 则{a =-tana,① h =tanB.② a+m 由①得%ac由②得号+贺= 1 tanB' B m = 。m 1 1 tana+tanB o·h tang tanatanB ∴.h= tanatanβ Xm. ana+tanB
导航 则 𝒉 𝒂 = -𝐭𝐚𝐧𝜶,① 𝒉 𝒂+𝒎 = 𝐭𝐚𝐧𝜷.② 由①得 𝒂 𝒉 =- 𝟏 𝐭𝐚𝐧𝜶 ,由②得 𝒂 𝒉 + 𝒎 𝒉 = 𝟏 𝐭𝐚𝐧𝜷 , ∴ 𝒎 𝒉 = 𝟏 𝐭𝐚𝐧𝜶 + 𝟏 𝐭𝐚𝐧𝜷 = 𝐭𝐚𝐧𝜶+𝐭𝐚𝐧𝜷 𝐭𝐚𝐧𝜶𝐭𝐚𝐧𝜷 . ∴h= 𝐭𝐚𝐧𝜶𝐭𝐚𝐧𝜷 𝐭𝐚𝐧𝜶+𝐭𝐚𝐧𝜷 ×m. 解:如图,B,C,D三点共线,测出∠ACD=α,∠ADC=β,CD=m.设 AB=h,BC=a

以梦为马 不负韶华!
以梦为马, 不负韶华!