
全程设计 第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.3 向量的减法
第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.3 向量的减法

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 一、向量的减法 【问题思考】 1.若小明从家去学校用a表示,从家到超市用b表示,从学校去 超市用c表示,你知道a,b,c是什么关系吗? 提示:c=b-a.(或a+c=b)
导航 课前·基础认知 一、向量的减法 【问题思考】 1.若小明从家去学校用a表示,从家到超市用b表示,从学校去 超市用c表示,你知道a,b,c是什么关系吗? 提示:c=b-a.(或a+c=b)

导 2.填空:(1)一般地,平面上任意给定两个向量a,b,如果向量x能 够满足b+x=a,则称x为向量a与b的,并记作x= (2)在平面内任取一点O,作0A=a,0B=b,作出向量BA,向量BA就 是向量a与b的差(也称BA为向量a与b的差向量),即OA一 OB=BA这种求两向量差的作图方法也常称为向量减法的三 角形法则. 3.两个向量的差是向量还是实数? 提示:向量
导航 2.填空:(1)一般地,平面上任意给定两个向量a,b,如果向量x能 够满足b+x=a,则称x为向量a与b的差,并记作x= a-b . (2)在平面内任取一点 O,作𝑶 𝑨 =a,𝑶 𝑩 =b,作出向量𝑩 𝑨 ,向量𝑩 𝑨 就 是向量 a 与 b 的差(也称𝑩 𝑨 为向量 a 与 b 的差向量),即𝑶 𝑨 − 𝑶 𝑩 = 𝑩 𝑨 .这种求两向量差的作图方法也常称为向量减法的三 角形法则. 3.两个向量的差是向量还是实数? 提示:向量
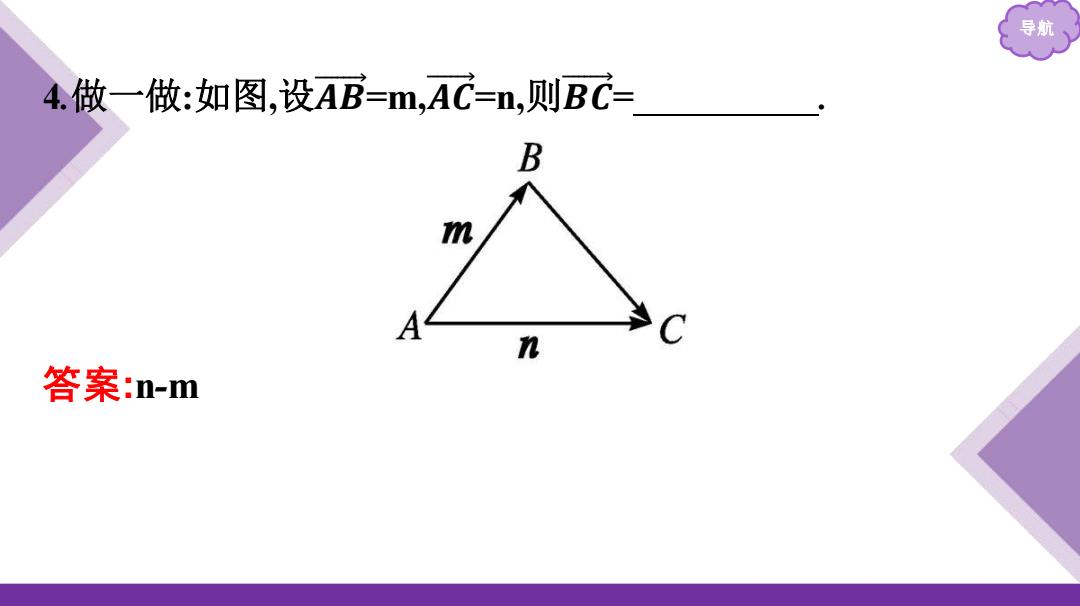
导航 4.做一做:如图,设AB=m,AC=n,则BC= B m A n C 答案:n-m
导航 4.做一做:如图,设𝑨 𝑩 =m,𝑨 𝑪 =n,则𝑩 𝑪 = . 答案:n-m

导航 二、相反向量 【问题思考】 1.物理中的力与其反作用力是什么关系? 提示:大小相等,方向相反 2.填空: (1)相反向量的定义: 与向量a方向 的向量称为a的相反向量,记作
导航 二、相反向量 【问题思考】 1.物理中的力与其反作用力是什么关系? 提示:大小相等,方向相反. 2.填空: (1)相反向量的定义: 与向量a方向相反、大小相等的向量称为a的相反向量,记作 -a

导航 2)相反向量的性质: ①at(-a)=(-a)+a=0; ②-(-a)=a; ③零向量的相反向量仍是0,即0=-0. (3)向量减法的理解: 向量的减法也可以看成向量的加法的逆运算,即a-b=a+(-b), 也就是:一个向量减去另一个向量,等于第一个向量加上第二 个向量的
导航 (2)相反向量的性质: ①a+(-a)=(-a)+a=0; ②-(-a)=a; ③零向量的相反向量仍是0,即0=-0. (3)向量减法的理解: 向量的减法也可以看成向量的加法的逆运算,即a-b=a+(-b), 也就是:一个向量减去另一个向量,等于第一个向量加上第二 个向量的相反向量

导航 3.做一做:AB+BC的相反向量是 答案:CA
导航 3.做一做:𝑨 𝑩 + 𝑩 𝑪 的相反向量是 . 答案:𝑪 𝑨

导航 课堂·重难突破 探究一向量加减法的几何作图 【例1】如图,点O是四边形ABCD内任一 点,试根据图中给出的向量,确定a,b,c,d的 a 方向(用箭头表示),使a+b=BA,c-d=DC,并 b B d 画出b-c和a+d. 分析:利用三角形法则和平行四边形法则 C 作图
导航 课堂·重难突破 探究一 向量加减法的几何作图 【例1】如图,点O是四边形ABCD内任一 点,试根据图中给出的向量,确定a,b,c,d的 方向(用箭头表示),使a+b= ,并 画出b-c和a+d. 分析:利用三角形法则和平行四边形法则 作图. 𝑩 𝑨 ,c-d=𝑫 𝑪
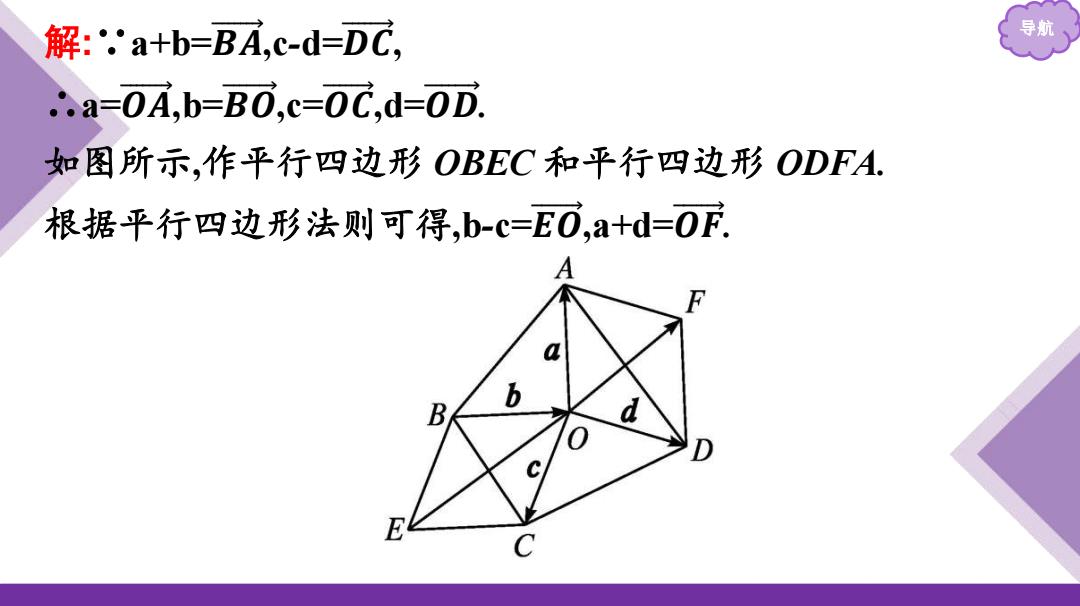
解:,a+b=BA,c-d=DC, 导航 ..a=0A,b-BO,c=0C,d=0D. 如图所示,作平行四边形OBEC和平行四边形ODFA. 根据平行四边形法则可得,b-c=EO,a+d=O下 A a b B d E C
导航 解:∵a+b=𝑩 𝑨 ,c-d=𝑫 𝑪 , ∴a=𝑶 𝑨 ,b=𝑩 𝑶 ,c=𝑶 𝑪 ,d=𝑶 𝑫 . 如图所示,作平行四边形 OBEC 和平行四边形 ODFA. 根据平行四边形法则可得,b-c=𝑬 𝑶 ,a+d=𝑶 𝑭