
全程设计 第六章 平面向量初步 6.3 平面向量线性运算的应用
第六章 平面向量初步 6.3 平面向量线性运算的应用

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 向量在平面几何中的应用 【问题思考】 1.证明线段平行问题,常用向量平行(共线)的等价条件:若 a=(c1y1),b=(c2y2),则alb(b≠0)台 → 2.求线段的长度或证明线段相等,可利用向量的线性运算、向 量模的公式a=√x2+y2(a=(xy)
导航 课前·基础认知 一、向量在平面几何中的应用 【问题思考】 1.证明线段平行问题,常用向量平行(共线)的等价条件:若 a=(x1 ,y1 ),b=(x2 ,y2 ),则a∥b(b≠0)⇔ a=λb ⇔ x1 y2=x2 y1 . 2.求线段的长度或证明线段相等,可利用向量的线性运算、向 量模的公式|a|= 𝒙 (a=(x,y)). 𝟐 + 𝒚 𝟐

导航 二、向量在物理中的应用 【问题思考】 涉及力、速度、加速度等物理量的运算问题可利用向量的知 识求解
导航 二、向量在物理中的应用 【问题思考】 涉及力、速度、加速度等物理量的运算问题可利用向量的知 识求解
导航 课堂·重难突破 探究一利用向量解决平面几何中的平行问题 【例1】如图,已知AC,BD是梯形ABCD的对角线,E,F分别是 BD,AC的中点,求证:EF Il BC. E B C
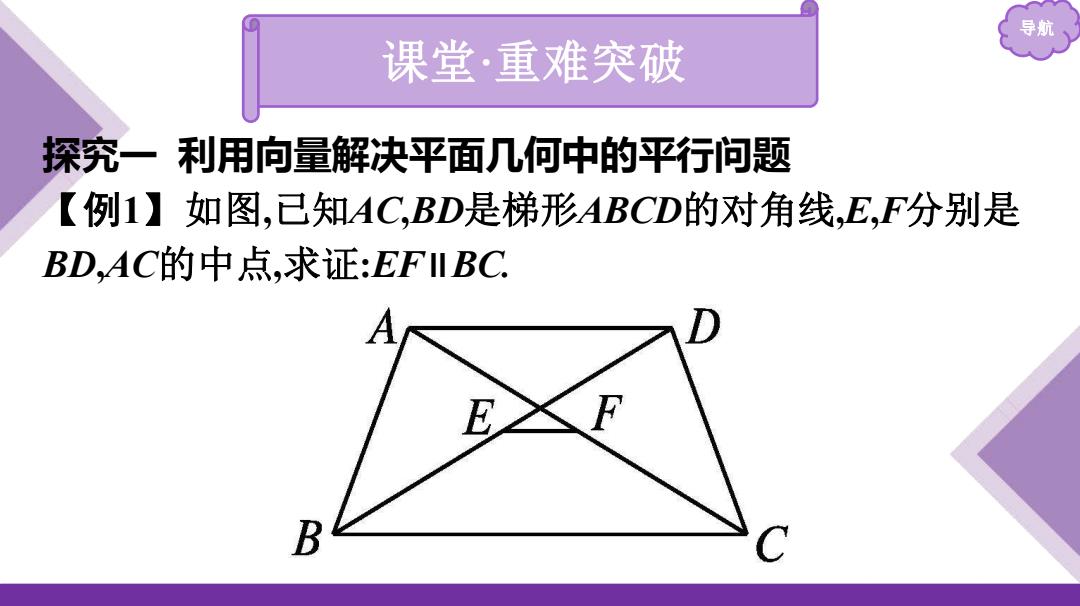
导航 课堂·重难突破 探究一 利用向量解决平面几何中的平行问题 【例1】如图,已知AC,BD是梯形ABCD的对角线,E,F分别是 BD,AC的中点,求证:EF∥BC

证明:设AB=a,AD=b,则BD=AD-AB=b-a 导航 AD BC,.BC=AD=b(≠0). E为BD的中点,BE=B而=b- 连接BF.,F是AC的中点, ..BF=(BA+BC)(BC-AB)-(2b-a). ..EF=BF-BE=(b-a)(b-a) =(-2)b-((经a-)2BC, ∴.EF‖BC B 又E,F,B,C四点不共线,.EF∥BC
导航 证明:设𝑨 𝑩 =a,𝑨 𝑫 =b,则𝑩 𝑫 = 𝑨 𝑫 − 𝑨 𝑩 =b-a. ∵𝑨 𝑫 ∥ 𝑩 𝑪 ,∴𝑩 𝑪 =λ𝑨 𝑫 =λb(λ≠0). ∵E 为 BD 的中点,∴𝑩 𝑬 = 𝟏 𝟐 𝑩 𝑫 = 𝟏 𝟐 (b-a). 连接 BF.∵F 是 AC 的中点, ∴𝑩 𝑭 = 𝟏 𝟐 (𝑩 𝑨 + 𝑩 𝑪 )= 𝟏 𝟐 (𝑩 𝑪 − 𝑨 𝑩 )= 𝟏 𝟐 (λb-a). ∴𝑬 𝑭 = 𝑩 𝑭 − 𝑩 𝑬 = 𝟏 𝟐 (λb-a)- 𝟏 𝟐 (b-a) = 𝟏 𝟐 𝝀 − 𝟏 𝟐 b= 𝟏 𝟐 𝝀- 𝟏 𝟐 · 𝟏 𝝀 𝑩 𝑪 , ∴𝑬 𝑭 ∥ 𝑩 𝑪 . 又 E,F,B,C 四点不共线,∴EF∥BC

延伸探究 导期 试用坐标法证明本例题 证明:如图,建立平面直角坐标系 由题意,设B(0,0),C(m,0),A(,t),D(,), 由中点坐标公式,得E吃》F(生,), (B) 承=((0酽1元 又E,F,B,C四点不共线,.EF∥BC 反思感悟平面几何中证明两直线平行问题,可转化为证明向 量共线问题,即寻找一个实数2,使得一个向量可以用另一个向 量的2倍表示,也可以通过坐标运算进行
导航 试用坐标法证明本例题. 证明:如图,建立平面直角坐标系. 由题意,设B(0,0),C(m,0),A(s,t),D(r,t). 由中点坐标公式,得 E 𝒓 𝟐 , 𝒕 𝟐 ,F 𝒎+𝒔 𝟐 , 𝒕 𝟐 , ∴𝑬 𝑭 = 𝒎+𝒔-𝒓 𝟐 ,𝟎 ,∴𝑬 𝑭 ∥ 𝑩 𝑪 . 又 E,F,B,C 四点不共线,∴EF∥BC. 反思感悟 平面几何中证明两直线平行问题,可转化为证明向 量共线问题,即寻找一个实数λ,使得一个向量可以用另一个向 量的λ倍表示,也可以通过坐标运算进行
【变式训练1】已知AD,BE,CF是△ABC的三条高,它们交于航 点O,DG⊥BE于点G,DH⊥CF于点H.求证:HGIEE 证明:.DG⊥BE,AE⊥BE, .GD∥AC,∴.GD I AC. 由已知条件可证得△AOE∽△DOG, 同理△AOF∽△DOH. 设0A=20D(0≠0), 则A正=DG,同理可得AF=D五, ..FE=AE-AF=DG-DH=A(DG-DH)=HG..'.HG FE, 又H,G,F,E四点不共线,.HG∥FE
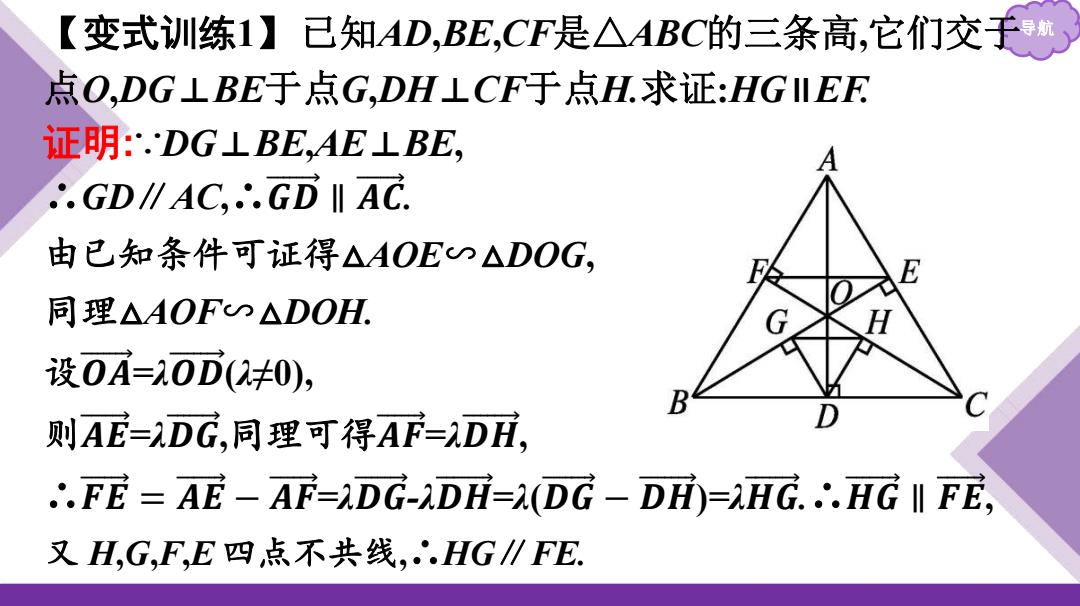
【变式训练 导航 1】已知AD,BE,CF是△ABC的三条高,它们交于 点O,DG⊥BE于点G,DH⊥CF于点H.求证:HG∥EF. 证明:∵DG⊥BE,AE⊥BE, ∴GD∥AC,∴𝑮 𝑫 ∥ 𝑨 𝑪 . 由已知条件可证得△AOE∽△DOG, 同理△AOF∽△DOH. 设𝑶 𝑨 =λ𝑶 𝑫 (λ≠0), 则𝑨 𝑬 =λ𝑫 𝑮 ,同理可得𝑨 𝑭 =λ𝑫 𝑯 , ∴𝑭 𝑬 = 𝑨 𝑬 − 𝑨 𝑭 =λ𝑫 𝑮 -λ𝑫 𝑯 =λ(𝑫 𝑮 − 𝑫 𝑯 )=λ𝑯 𝑮 .∴𝑯 𝑮 ∥ 𝑭 𝑬 , 又 H,G,F,E 四点不共线,∴HG∥FE

探究二证明三点共线问题 导航 【例2】如图,点O是平行四边形ABCD的中心,E,F分别在边 CD1B上,号=5=求证:点E,0F在同-直线上 E A B 分析:要证,点E,O,F共线,只需证FO=m0E(m∈R), 可选用基底AB,AD来表示FO及OE,进而可使问题得到解决
导航 分析:要证点 E,O,F 共线,只需证𝑭 𝑶 =m𝑶 𝑬 (m∈R), 可选用基底𝑨 𝑩 ,𝑨 𝑫 来表示𝑭 𝑶 及𝑶 𝑬 ,进而可使问题得到解决. 探究二 证明三点共线问题 【例2】如图,点O是平行四边形ABCD的中心,E,F分别在边 CD,AB 上,且 𝑪𝑬 𝑬𝑫 = 𝑨𝑭 𝑭𝑩 = 𝟏 𝟐 ,求证:点 E,O,F 在同一直线上

证明:设丽=,A丽b,由EF分别在边CD,B上,号 AF 2 得F0=FA+A0-+号AC-含a+a+b) 2a+2b, OE -OC+CE=AC+CD=(a+b) 1 .F0=0E. 又O为其公共点,∴点E,O,F在同一直线上 反思感悟要证明三点共线,只需要证明包含这三个点的两个 向量共线,从而把点共线问题转化成向量共线问题
导航 证明:设𝑨 𝑩 =a,𝑨 𝑫 =b,由 E,F 分别在边 CD,AB 上,且 𝑪𝑬 𝑬𝑫 = 𝑨𝑭 𝑭𝑩 = 𝟏 𝟐 , 得𝑭 𝑶 = 𝑭 𝑨 + 𝑨 𝑶 =- 𝟏 𝟑 a+ 𝟏 𝟐 𝑨 𝑪 =- 𝟏 𝟑 a+ 𝟏 𝟐 (a+b)= 𝟏 𝟔 a+ 𝟏 𝟐 b, 𝑶 𝑬 = 𝑶 𝑪 + 𝑪 𝑬 = 𝟏 𝟐 𝑨 𝑪 + 𝟏 𝟑 𝑪 𝑫 = 𝟏 𝟐 (a+b)- 𝟏 𝟑 a= 𝟏 𝟔 a+ 𝟏 𝟐 b. ∴𝑭 𝑶 = 𝑶 𝑬 . 又O为其公共点,∴点E,O,F在同一直线上. 反思感悟 要证明三点共线,只需要证明包含这三个点的两个 向量共线,从而把点共线问题转化成向量共线问题