
全程设计 复习课 第3课时 立体几何步
复习课 第3课时 立体几何初步

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破
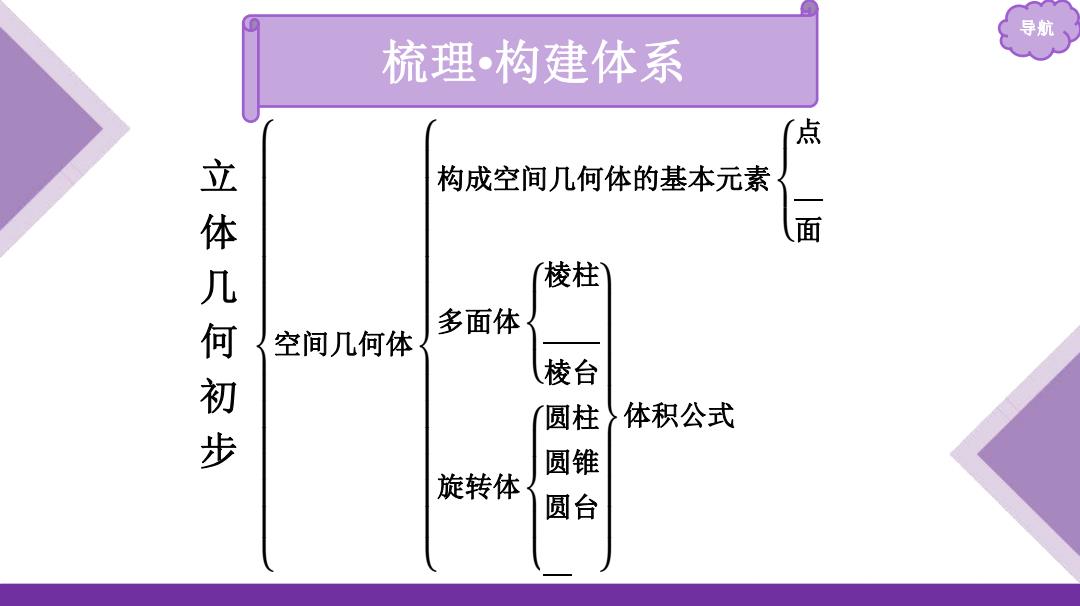
导航 梳理•构建体系 点 构成空间几何体的基本元素 立体几何初步 面 棱柱 多面体 空间几何体 棱台 圆柱 体积公式 圆锥 旋转体 圆台
导航 梳理 •构建体系 立体几何初步 空间几何体 构成空间几何体的基本元素 点线面 多面体 棱柱 棱锥 棱台 旋转体 圆柱 圆锥 圆台球 体积公式
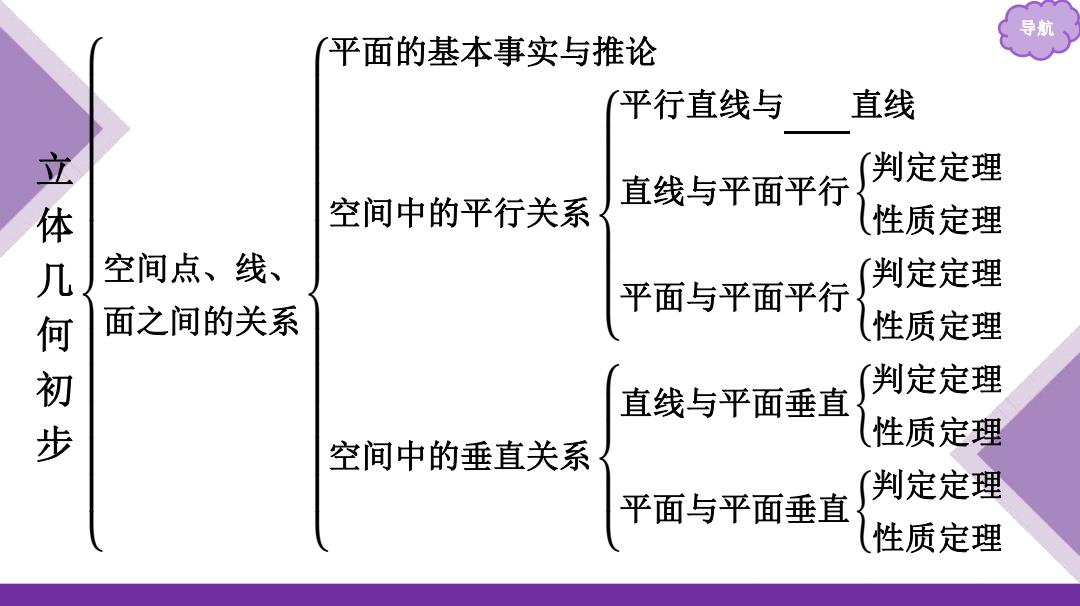
导期 平面的基本事实与推论 平行直线与 直线 判定定理 立体几何初步 空间中的平行关系 直线与平面平行 性质定理 空间点、线、 判定定理 平面与平面平行 面之间的关系 性质定理 判定定理 直线与平面垂直 性质定理 空间中的垂直关系 判定定理 平面与平面垂直 性质定理
导航 立体几何初步 空间点、线、 面之间的关系 平面的基本事实与推论 空间中的平行关系 平行直线与异面直线 直线与平面平行 判定定理 性质定理 平面与平面平行 判定定理 性质定理 空间中的垂直关系 直线与平面垂直 判定定理 性质定理 平面与平面垂直 判定定理 性质定理

要点梳理 1用斜二测画法作图时应着重把握哪两点? 提示:(1)在平面图形中互相垂直的x轴和y轴,在直观图中作出与之 对应的x'轴和y'轴,使得它们正方向的夹角为45°(或135°) (2)平面图形中与x轴平行(或重合)的线段画成与x'轴平行(或重合) 的线段,且长度不变 平面图形中与y轴平行(或重合)的线段画成与y轴平行(或重合)的 线段,且长度为原来长度的一半 2.构成空间几何体的基本元素有哪些? 提示:点、线、面
导航 要点梳理 1.用斜二测画法作图时应着重把握哪两点? 提示:(1)在平面图形中互相垂直的x轴和y轴,在直观图中作出与之 对应的x'轴和y'轴,使得它们正方向的夹角为45°(或135°). (2)平面图形中与x轴平行(或重合)的线段画成与x'轴平行(或重合) 的线段,且长度不变. 平面图形中与y轴平行(或重合)的线段画成与y'轴平行(或重合)的 线段,且长度为原来长度的一半. 2.构成空间几何体的基本元素有哪些? 提示:点、线、面
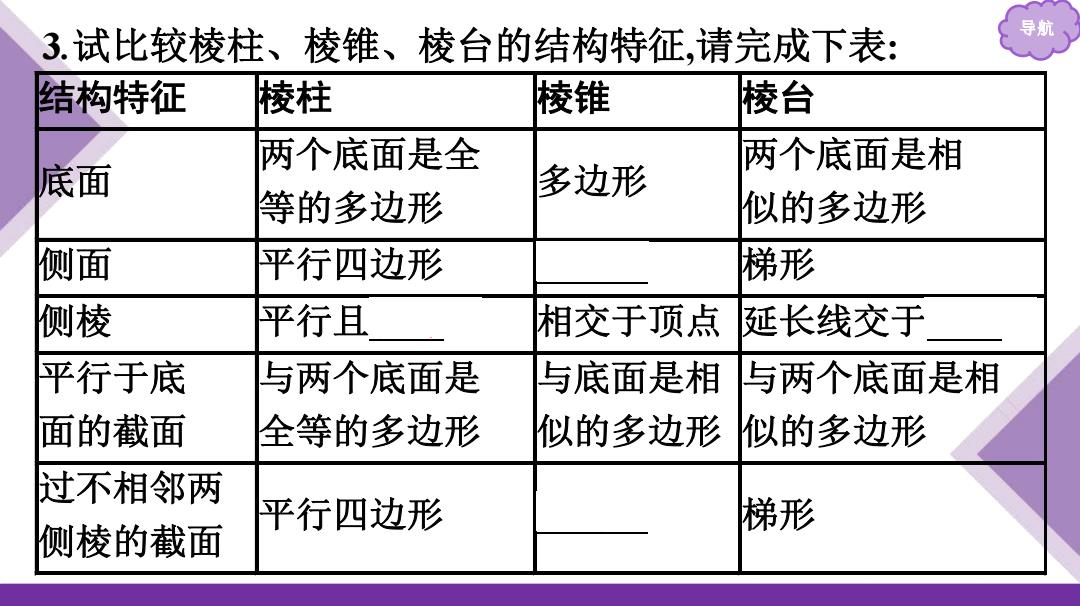
3.试比较棱柱、棱锥、棱台的结构特征,请完成下表: 导航、 结构特征 棱柱 棱锥 棱台 两个底面是全 两个底面是相 底面 多边形 等的多边形 似的多边形 侧面 平行四边形 梯形 侧棱 平行且 相交于顶点 延长线交于 平行于底 与两个底面是 与底面是相 与两个底面是相 面的截面 全等的多边形 似的多边形 似的多边形 过不相邻两 平行四边形 梯形 侧棱的截面
导航 3.试比较棱柱、棱锥、棱台的结构特征,请完成下表: 结构特征 棱柱 棱锥 棱台 底面 两个底面是全 等的多边形 多边形 两个底面是相 似的多边形 侧面 平行四边形 三角形 梯形 侧棱 平行且相等 相交于顶点 延长线交于一点 平行于底 面的截面 与两个底面是 全等的多边形 与底面是相 似的多边形 与两个底面是相 似的多边形 过不相邻两 侧棱的截面 平行四边形 三角形 梯形

导航 4.常见的四棱柱(长方体、直平行六面体、正方体、平行六 面体、正四棱柱、四棱柱)的关系是怎样的?
导航 4.常见的四棱柱(长方体、直平行六面体、正方体、平行六 面体、正四棱柱、四棱柱)的关系是怎样的?
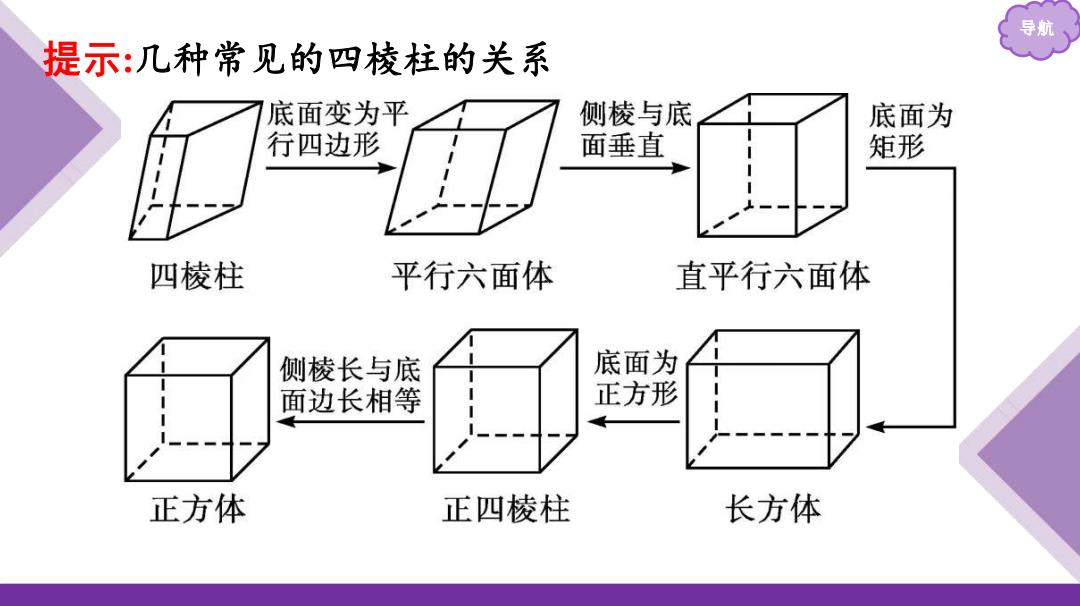
导航 提示:几种常见的四棱柱的关系 底面变为平 侧棱与底 底面为 行四边形 面垂直 矩形 四棱柱 平行六面体 直平行六面体 侧棱长与底 底面为 面边长相等 正方形 正方体 正四棱柱 长方体
导航 提示 :几种常见的四棱柱的关系
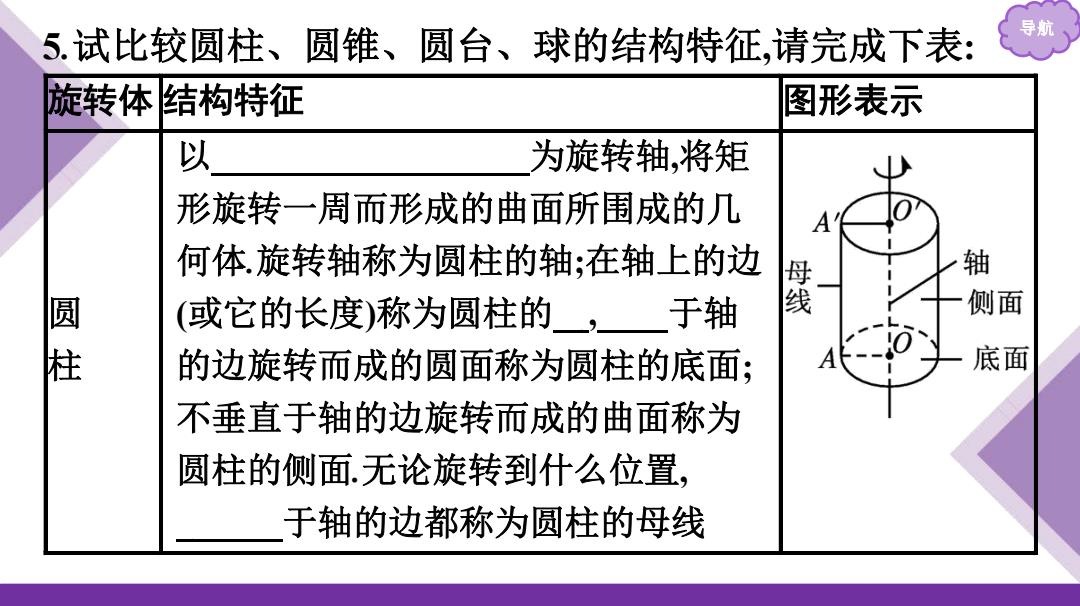
导 5.试比较圆柱、圆锥、圆台、球的结构特征,请完成下表: 旋转体结构特征 图形表示 以 为旋转轴,将矩 形旋转一周而形成的曲面所围成的几 何体.旋转轴称为圆柱的轴;在轴上的边 屋 轴 (或它的长度)称为圆柱的,于轴 侧面 圆柱 的边旋转而成的圆面称为圆柱的底面; 底面 不垂直于轴的边旋转而成的曲面称为 圆柱的侧面.无论旋转到什么位置, 于轴的边都称为圆柱的母线
导航 5.试比较圆柱、圆锥、圆台、球的结构特征,请完成下表: 旋转体 结构特征 图形表示 圆 柱 以矩形的一边所在直线为旋转轴,将矩 形旋转一周而形成的曲面所围成的几 何体.旋转轴称为圆柱的轴;在轴上的边 (或它的长度)称为圆柱的高,垂直于轴 的边旋转而成的圆面称为圆柱的底面; 不垂直于轴的边旋转而成的曲面称为 圆柱的侧面.无论旋转到什么位置, 不垂直于轴的边都称为圆柱的母线
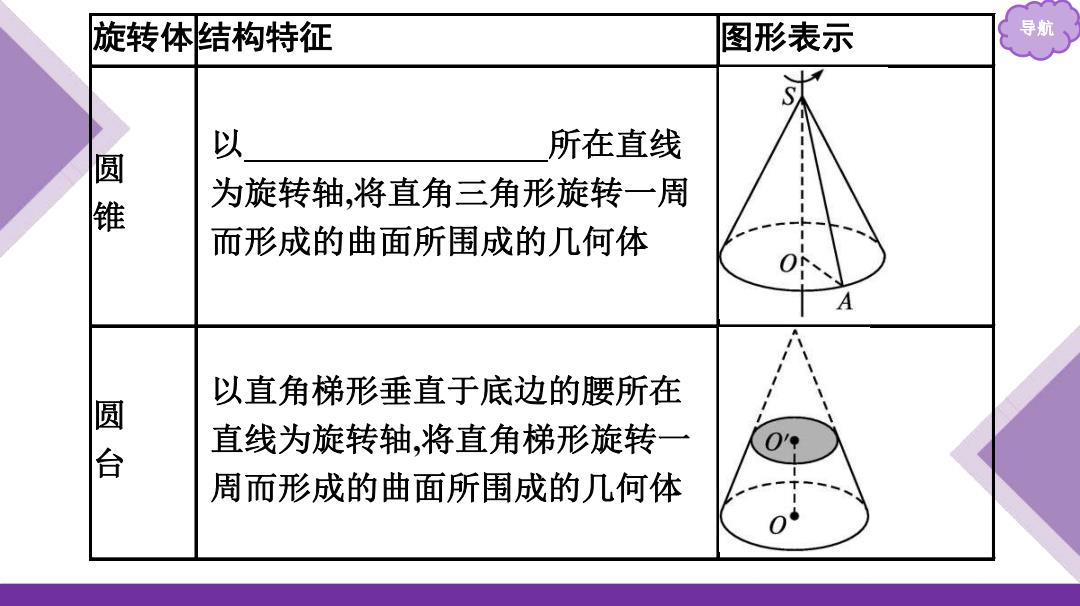
旋转体结构特征 图形表示 导航、 以 所在直线 圆锥 为旋转轴,将直角三角形旋转一周 而形成的曲面所围成的几何体 A 以直角梯形垂直于底边的腰所在 圆 直线为旋转轴,将直角梯形旋转一 周而形成的曲面所围成的几何体
旋转体结构特征 图形表示 导航 圆 锥 以直角三角形一直角边所在直线 为旋转轴,将直角三角形旋转一周 而形成的曲面所围成的几何体 圆 台 以直角梯形垂直于底边的腰所在 直线为旋转轴,将直角梯形旋转一 周而形成的曲面所围成的几何体