
全程设计 第十一章立体几何初步 11.4 空间中的垂直关系 11.4.2 平面与平面垂直
第十一章立体几何初步 11.4 空间中的垂直关系 11.4.2 平面与平面垂直
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解二面角的定义 2.了解面面垂直的定义, 3.掌握面面垂直的判定定理和性质定理,并能灵活应用定理解 决一些简单问题 4.体会数学抽象的过程;加强逻辑推理能力的培养
导航 课标定位素养阐释 1.了解二面角的定义. 2.了解面面垂直的定义. 3.掌握面面垂直的判定定理和性质定理,并能灵活应用定理解 决一些简单问题. 4.体会数学抽象的过程;加强逻辑推理能力的培养

导航 课前·基础认知 一、二面角 【问题思考】 1.两条相交直线我们可以用它们的夹角刻画它们的状态,那么 两个相交平面能否借助于角来刻画它们的情况呢? 提示:能
导航 课前·基础认知 一、二面角 【问题思考】 1.两条相交直线我们可以用它们的夹角刻画它们的状态,那么 两个相交平面能否借助于角来刻画它们的情况呢? 提示:能

导航 2.填空: (1)二面角的定义:平面内的一条直线把一个平面分成两部分, 其中的每一部分都称为一个从一条直线出发的两个 所组成的图形称为二面角,这条 称为二面角的棱, 这两个半平面称为二面角的面
导航 2.填空: (1)二面角的定义:平面内的一条直线把一个平面分成两部分, 其中的每一部分都称为一个半平面.从一条直线出发的两个 半平面所组成的图形称为二面角,这条直线称为二面角的棱, 这两个半平面称为二面角的面
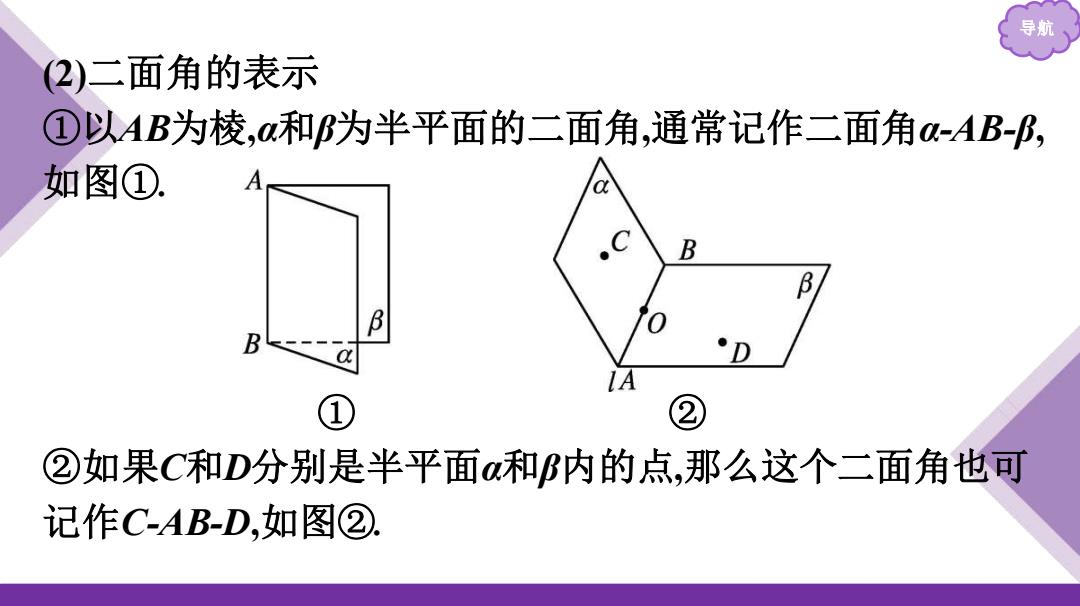
导 2)二面角的表示 ①以AB为棱,a和B为半平面的二面角,通常记作二面角a-AB-B, 如图①. B B B ②如果C和D分别是半平面a和B内的点,那么这个二面角也可 记作CAB-D,如图②
导航 (2)二面角的表示 ①以AB为棱,α和β为半平面的二面角,通常记作二面角α-AB-β, 如图①. ① ② ②如果C和D分别是半平面α和β内的点,那么这个二面角也可 记作C-AB-D,如图②

导航 3)二面角的平面角 在二面角a--的棱上任取一点O,以O为垂足,分别在半平面a 和B内作垂直于的射线OA和OB,则射线OA和OB所成的角 称为二面角的平面角.二面角的大小用它的 的大小来 度量,即二面角大小等于它的平面角大小.平面角是的二 面角称为直二面角
导航 (3)二面角的平面角 在二面角α-l-β的棱上任取一点O,以O为垂足,分别在半平面α 和β内作垂直于棱的射线OA和OB,则射线OA和OB所成的角 称为二面角的平面角.二面角的大小用它的平面角的大小来 度量,即二面角大小等于它的平面角大小.平面角是直角的二 面角称为直二面角
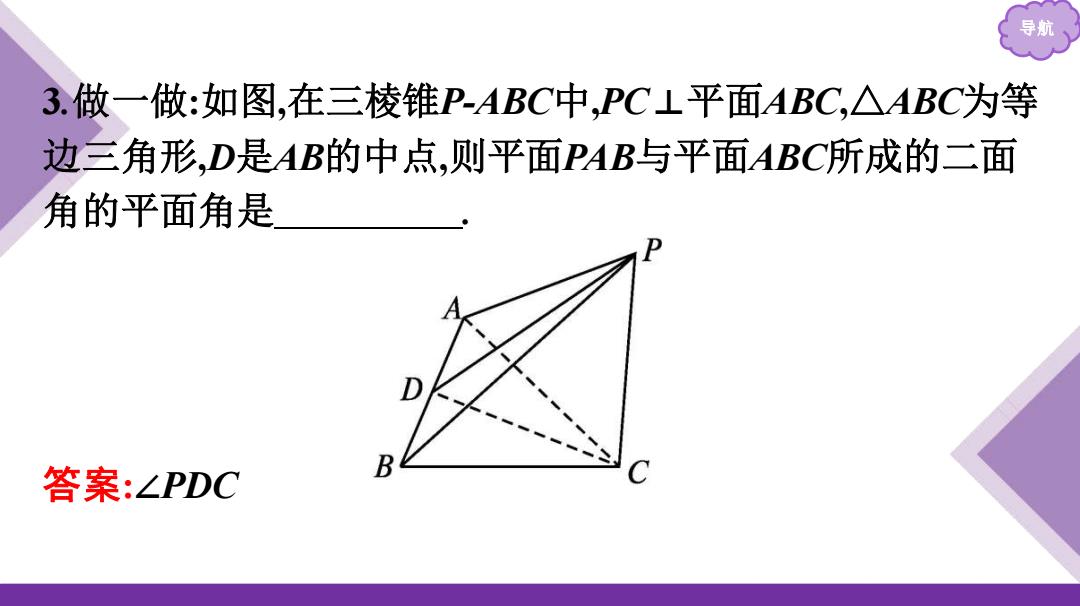
导航 3.做一做:如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为等 边三角形,D是AB的中点,则平面PAB与平面ABC所成的二面 角的平面角是 答案:∠PDC B
导航 3.做一做:如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为等 边三角形,D是AB的中点,则平面PAB与平面ABC所成的二面 角的平面角是 . 答案:∠PDC

导航 二、平面与平面垂直的判定定理 【问题思考】 1很多大型超市的门口装有旋转门,门轴所在直线与地面是垂 直的,门在旋转时,门扇与地面是否始终垂直? 提示:是
导航 二、平面与平面垂直的判定定理 【问题思考】 1.很多大型超市的门口装有旋转门,门轴所在直线与地面是垂 直的,门在旋转时,门扇与地面是否始终垂直? 提示:是

导 2.填空: (1)平面与平面垂直的定义:如果两个平面a与所成角的大小 为 ,则称这两个平面互相垂直,记作 (2)面面垂直的判定定理 文字语言 图形表示 符号语言 如果一个平面经过另外一 个平面的 ,那么这 1B →⊥ 两个平面互相垂直
导航 2.填空: (1)平面与平面垂直的定义:如果两个平面α与β所成角的大小 为 90° ,则称这两个平面互相垂直,记作α⊥β . (2)面面垂直的判定定理 文字语言 图形表示 符号语言 如果一个平面经过另外一 个平面的一条垂线,那么这 两个平面互相垂直 𝐥 ⊂ 𝛂 𝐥 ⊥ 𝛃 ⇒ 𝜶 ⊥β