
全程设计 第一章 空间向量与立体几何 1.2空间向量在立体几何中的应用 1.2.4二面角
第一章 空间向量与立体几何 1.2 空间向量在立体几何中的应用 1.2.4 二面角
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.了解二面角及其平面角的概念 2.掌握求二面角的两种方法:几何法和向量法」 3.体会数学抽象的过程,加强逻辑推理和数学运算能力的培养
导航 课标定位素养阐释 1.了解二面角及其平面角的概念. 2.掌握求二面角的两种方法:几何法和向量法. 3.体会数学抽象的过程,加强逻辑推理和数学运算能力的培养

导航 课前·基础认知 一、二面角及其度量 【问题思考】 1.将课本的封面绕书脊旋转少许与将封面掀开并展开,两者状 态不一样,可如何刻画掀开封面的不同状态? 提示:可用旋转的角度
导航 课前·基础认知 一、二面角及其度量 【问题思考】 1.将课本的封面绕书脊旋转少许与将封面掀开并展开,两者状 态不一样,可如何刻画掀开封面的不同状态? 提示:可用旋转的角度

导航 2.填空:(1)二面角的定义 平面内的一条直线把一个平面分成两部分,其中的每一部分 都称为一个半平面. 从一条直线出发的两个半平面所组成的图形称为,这 条直线称为 ,这两个半平面称为二面角的
导航 2.填空:(1)二面角的定义 平面内的一条直线把一个平面分成两部分,其中的每一部分 都称为一个半平面. 从一条直线出发的两个半平面所组成的图形称为二面角,这 条直线称为二面角的棱,这两个半平面称为二面角的面
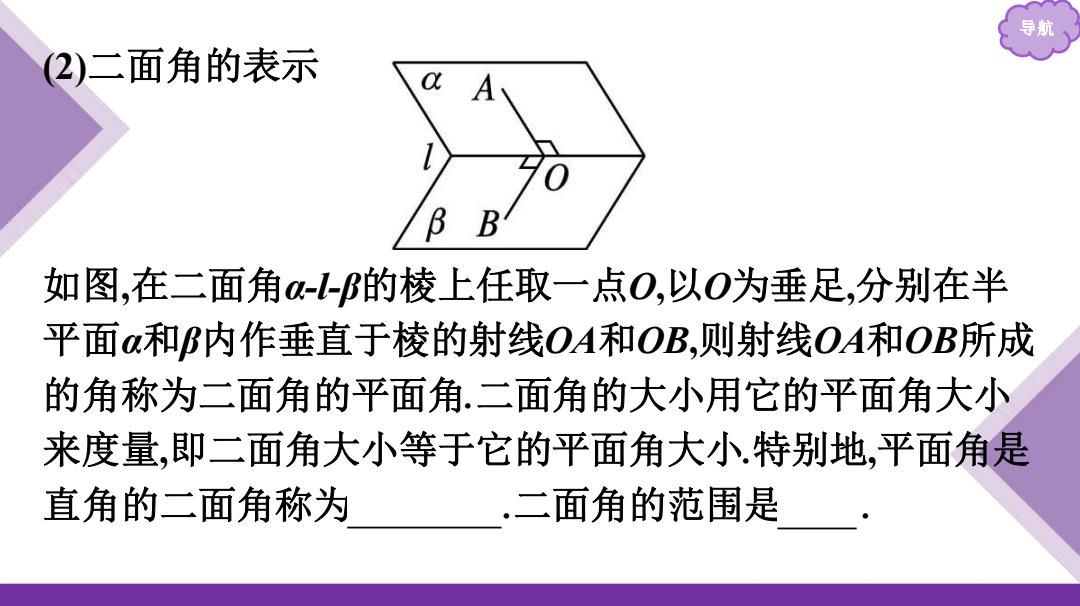
导航 2)二面角的表示 如图,在二面角-1-的棱上任取一点O,以O为垂足,分别在半 平面a和B内作垂直于棱的射线OA和OB,则射线OA和OB所成 的角称为二面角的平面角.二面角的大小用它的平面角大小 来度量,即二面角大小等于它的平面角大小特别地,平面角是 直角的二面角称为 .二面角的范围是
导航 (2)二面角的表示 如图,在二面角α-l-β的棱上任取一点O,以O为垂足,分别在半 平面α和β内作垂直于棱的射线OA和OB,则射线OA和OB所成 的角称为二面角的平面角.二面角的大小用它的平面角大小 来度量,即二面角大小等于它的平面角大小.特别地,平面角是 直角的二面角称为直二面角.二面角的范围是[0,π]

导航 3做一做:在正方体ABCD-A1BCD1中,二面角A-CD1-C的平 面角是( A.∠AD1D B.∠AD1C C.∠AC1C D.∠D1C1C 答案:A
导航 3.做一做:在正方体ABCD-A1B1C1D1中,二面角A-C1D1 -C的平 面角是( ) A.∠AD1D B.∠AD1C C.∠AC1C D.∠D1C1C 答案:A

导 二、用平面的法向量求二面角 【问题思考】 1.已知二面角的两个半平面的法向量分别为n1,n2,则二面角的 大小与一定相等吗? 提示:不一定.二面角的大小与相等或互补 2.填空:如果向量n1n2分别是二面角的两个半平面的一个法 向量,设二面角的大小为0,则0= ,特别 地,sin0=sin
导航 二、用平面的法向量求二面角 【问题思考】 1.已知二面角的两个半平面的法向量分别为n1 ,n2 ,则二面角的 大小与一定相等吗? 提示:不一定.二面角的大小与相等或互补. 2.填空:如果向量n1 ,n2分别是二面角的两个半平面的一个法 向量,设二面角的大小为θ,则θ=或θ=π-,特别 地,sin θ=sin

导航 3.做一做:设a=(0,1,1),b=(1,0,1)分别是平面a,的两个法向量, 则锐二面角a--的大小是() A.45° B.90° C.60°D.120° 解析:设锐二面角a--B的大小是0, 则cos0la-hl 1 lallbl 2故0=60° 答案:C
导航 3.做一做:设a=(0,1,1),b=(1,0,1)分别是平面α,β的两个法向量, 则锐二面角α-l-β的大小是( ) A.45° B.90° C.60°D.120° 解析:设锐二面角α-l-β的大小是θ, 答案:C 则 cos θ= |𝒂·𝒃| |𝒂||𝒃| = 𝟏 𝟐× 𝟐 = 𝟏 𝟐 ,故 θ=60°

导航 【思考辨析】 判断正误(正确的画“√,错误的画“×) (①)二面角的取值范围是[0,.( ) (2)若平面a,的法向量分别为n1,2,则等于二面角的大 小.( 3)平面角是直角的二面角叫直二面角.( (4)任何一个二面角有很多平面角.()
导航 【思考辨析】 判断正误.(正确的画“ ”,错误的画“×”) (1)二面角的取值范围是 .( × ) (2)若平面α,β的法向量分别为n1 ,n2 ,则等于二面角的大 小.( × ) (3)平面角是直角的二面角叫直二面角.( ) (4)任何一个二面角都有很多平面角.( ) 𝟎, 𝛑 𝟐