
全程设计 第一章 空间向量与立体几何 1.2 空间向量在立体几何中的应用 1.2.5空间中的距离
第一章 空间向量与立体几何 1.2 空间向量在立体几何中的应用 1.2.5 空间中的距离
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导 课标定位素养阐释 1.了解空间中两点之间的距离、点到直线的距离及两平行平 面的距离等 2.能够利用向量法求各种空间距离 3.体会数学抽象的过程,加强逻辑推理及数学运算能力的培养
导航 课标定位素养阐释 1.了解空间中两点之间的距离、点到直线的距离及两平行平 面的距离等. 2.能够利用向量法求各种空间距离. 3.体会数学抽象的过程,加强逻辑推理及数学运算能力的培养

导航 课前·基础认知 -、 两点之间的距离 【问题思考】 1给定空间中不重合的两点A,B,以A,B为端点的曲线段有多 少条?是否存在长度最短的线段? 提示:无数.存在 2.填空:空间中两点之间的距离指的是这两个点连线的
导航 课前·基础认知 一、两点之间的距离 【问题思考】 1.给定空间中不重合的两点A,B,以A,B为端点的曲线段有多 少条?是否存在长度最短的线段? 提示:无数.存在. 2.填空:空间中两点之间的距离指的是这两个点连线的 线段长
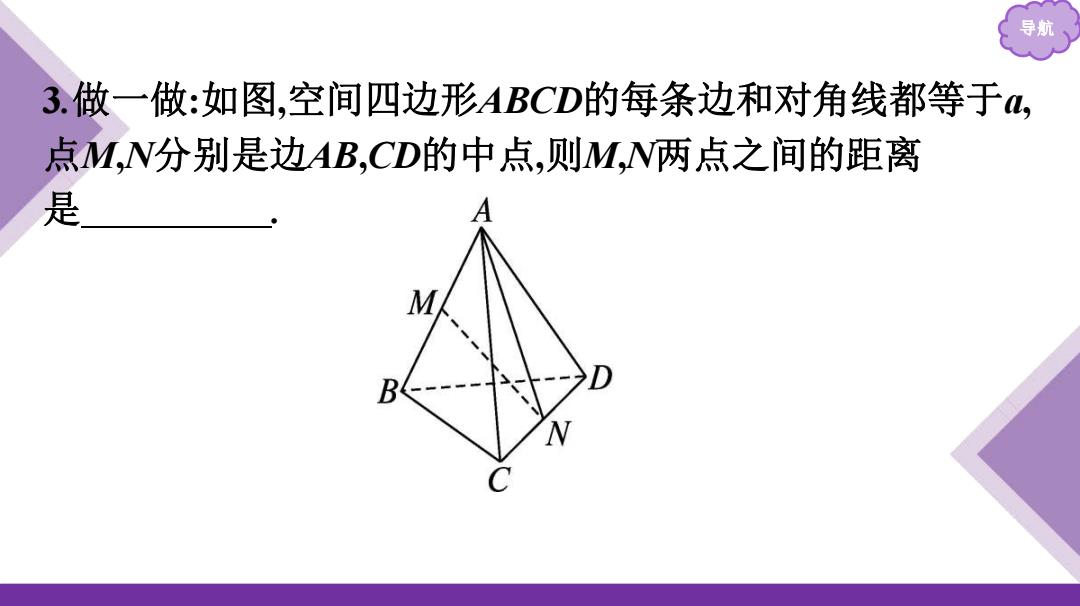
导航 3.做一做:如图,空间四边形ABCD的每条边和对角线都等于, 点MN分别是边AB,CD的中点,则M,N两点之间的距离 是 M B
导航 3.做一做:如图,空间四边形ABCD的每条边和对角线都等于a, 点M,N分别是边AB,CD的中点,则M,N两点之间的距离 是

导航 解析:设AB=p,AC=q,AD=r,则pl=q=r=a, 且p,q>==<,qP=60°, N-AN-A丽=aC+AD号AE=q+rp ..MNP-(q+r-p)-iq+r-+p+2(qr-qp-rpl “MM空,即M,N两点之间的距离为汽 答案
导航 解析:设𝑨 𝑩 =p,𝑨 𝑪 =q,𝑨 𝑫 =r,则|p|=|q|=|r|=a, 且===60°, ∴𝑴 𝑵 = 𝑨 𝑵 − 𝑨 𝑴 = 𝟏 𝟐 (𝑨 𝑪 + 𝑨 𝑫 )- 𝟏 𝟐 𝑨 𝑩 = 𝟏 𝟐 (q+r-p), ∴|𝑴 𝑵 | 2 = 𝟏 𝟒 (q+r-p)2 = 𝟏 𝟒 [q2 +r2 +p2 +2(q·r-q·p-r·p)]= 𝒂 𝟐 𝟐 , ∴|𝑴 𝑵 |= 𝟐 𝟐 a,即 M,N 两点之间的距离为 𝟐 𝟐 a. 答案: 𝟐 𝟐 a

导月 二、点到直线的距离 【问题思考】 1.已知点A在直线外,点P是直线L上的一个动点,AP是否存在 最小值?若存在,请说明AP最小时点P的位置 提示:存在.当APL时,AP存在最小值 2.填空:给定空间中一条直线及外一点A,因为与A能确定一 个平面,所以过A可以作直线的一条 ,这条 的长 称为点A到直线的距离. ()点到直线的距离是这个点与直线上点的最短 的长度 (2)如果点A是直线上的点,则约定A到直线的距离为
导航 二、点到直线的距离 【问题思考】 1.已知点A在直线l外,点P是直线l上的一个动点,AP是否存在 最小值?若存在,请说明AP最小时点P的位置. 提示:存在.当AP⊥l时,AP存在最小值. 2.填空:给定空间中一条直线l及l外一点A,因为l与A能确定一 个平面,所以过A可以作直线l的一条垂线段,这条垂线段的长 称为点A到直线l的距离. (1)点到直线的距离是这个点与直线上点的最短连线的长度. (2)如果点A是直线l上的点,则约定A到直线l的距离为0
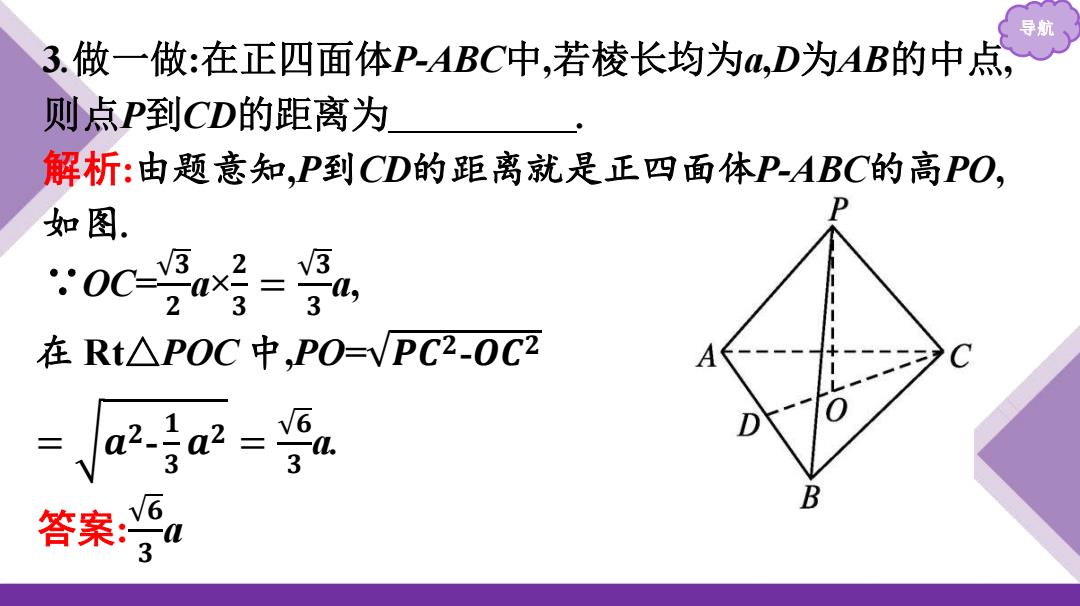
导 3.做一做:在正四面体P-ABC中,若棱长均为a,D为AB的中点, 则点P到CD的距离为 解析:由题意知,P到CD的距离就是正四面体P-ABC的高PO, 如图 OC- 2 2 =a, 3 在Rt△POC中,PO=VPC2-0C2 答案 B
导航 3.做一做:在正四面体P-ABC中,若棱长均为a,D为AB的中点, 则点P到CD的距离为 . 解析:由题意知,P到CD的距离就是正四面体P-ABC的高PO, 如图. ∵OC= 𝟑 𝟐 a× 𝟐 𝟑 = 𝟑 𝟑 a, 在 Rt△POC 中,PO= 𝑷𝑪𝟐-𝑶𝑪𝟐 = 𝒂𝟐- 𝟏 𝟑 𝒂𝟐 = 𝟔 𝟑 a. 答案: 𝟔 𝟑 a

导航 三、点到平面的距离 【问题思考】 1.若点P平面a,点M∈a,P在平面a内的射影为P,则PM与PPo 的大小关系如何? 提示:PMzPPo
导航 三、点到平面的距离 【问题思考】 1.若点P∉平面α,点M∈α,P在平面α内的射影为P0 ,则PM与PP0 的大小关系如何? 提示:PM≥PP0

2.填空:给定空间中一个平面a及a外一点A,过A可以作平面a 的一条 这条 的长称为点A到平面a的距离. ()点到平面的距离是这个点与平面内点的连线的长度: (2)如果点A是平面a内一点,则约定A到平面a的距离为· (3)若A是平面a外一点,B是平面a内一点,n是平面a的一个法 向量,则点A到平面的距离d=
导航 2.填空:给定空间中一个平面α及α外一点A,过A可以作平面α 的一条垂线段,这条垂线段的长称为点A到平面α的距离. (1)点到平面的距离是这个点与平面内点的最短连线的长度. (2)如果点A是平面α内一点,则约定A到平面α的距离为0 . (3)若A是平面α外一点,B是平面α内一点,n是平面α的一个法 向量,则点A到平面α的距离d= . |𝑩 𝑨 ·𝒏| |𝒏|