
全程设计 第一章 空间向量与立体几何 1.1 空间向量及其运算 1.1.1 空间向量及其运算 第1课时 空间向量的概念与运算
第一章 空间向量与立体几何 1.1 空间向量及其运算 1.1.1 空间向量及其运算 第1课时 空间向量的概念与运算
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.通过类比平面向量,掌握空间向量的有关概念 2.掌握空间向量的加法、减法与数乘运算. 3.体会数学抽象的过程,加强直观想象和逻辑推理、运算能力 的培养
导航 课标定位素养阐释 1.通过类比平面向量,掌握空间向量的有关概念. 2.掌握空间向量的加法、减法与数乘运算. 3.体会数学抽象的过程,加强直观想象和逻辑推理、运算能力 的培养

导航 课前·基础认知 一、 空间向量的概念 【问题思考】 1.在一个平面上,若两个非零向量a,b的方向相同,则aIb.将此 命题中的“在一个平面上”改为“在空间中”,命题是否仍成立? 提示:成立 2.将平面向量的有关概念与约定推广到空间中,是否仍成立? 提示:成立
导航 课前·基础认知 一、空间向量的概念 【问题思考】 1.在一个平面上,若两个非零向量a,b的方向相同,则a∥b.将此 命题中的“在一个平面上”改为“在空间中”,命题是否仍成立? 提示:成立. 2.将平面向量的有关概念与约定推广到空间中,是否仍成立? 提示:成立

导月 3.填空:(1)空间中既有 又有 的量称为空间向量(简称 为向量). (2)大小相等、 的向量称为相等的向量 (3)方向 的两个非零向量互相平行. (4)一般地,空间中的多个向量,如果表示它们的有向线段通过 平移之后,都能在 内,则称这些向量共面;否则,称这 些向量不共面
导航 3.填空:(1)空间中既有大小又有方向的量称为空间向量(简称 为向量). (2)大小相等、方向相同的向量称为相等的向量. (3)方向相同或者相反的两个非零向量互相平行. (4)一般地,空间中的多个向量,如果表示它们的有向线段通过 平移之后,都能在同一平面内,则称这些向量共面;否则,称这 些向量不共面

导航 4.做一做:如图,在长方体ABCD-A1B1C1D1中,AD=3,AA1=4, AB=5.在长方体的所有棱对应的向量中, B (1)与AA1相等的向量有 (2)与AA平行的向量有 (3)与AA,DC共面的向量有
导航 4.做一做:如图,在长方体ABCD-A1B1C1D1中,AD=3,AA1 =4, AB=5.在长方体的所有棱对应的向量中, (1)与𝑨𝑨𝟏 相等的向量有______________. (2)与𝑨𝑨𝟏 平行的向量有______________. (3)与𝑨𝑨𝟏 ,𝑫 𝑪 共面的向量有______________

导航 答案:(I)BB1,CC,DD1 (2)BBi,CCi,DDi,A1A,BiB,CiC,DiD 3A A,AB,BA,BB BB,A Bi,B AL CD,DD,DD.CCT CIC,DiC1,C1D1
导航 答案:(1)𝑩𝑩𝟏 , 𝑪𝑪𝟏 ,𝑫𝑫𝟏 (2)𝑩𝑩𝟏 ,𝑪𝑪𝟏 ,𝑫𝑫𝟏 ,𝑨 𝟏 𝑨 , 𝑩 𝟏 𝑩 , 𝑪 𝟏 𝑪 ,𝑫 𝟏 𝑫 (3)𝑨 𝟏 𝑨 ,𝑨 𝑩 , 𝑩 𝑨 , 𝑩𝑩𝟏 , 𝑩 𝟏 𝑩 ,𝑨𝟏 𝑩𝟏 , 𝑩𝟏 𝑨𝟏 ,𝑪 𝑫 , 𝑫𝑫𝟏 ,𝑫 𝟏 𝑫 ,𝑪𝑪𝟏 , 𝑪 𝟏 𝑪 ,𝑫𝟏 𝑪𝟏 ,𝑪𝟏 𝑫𝟏

导航 二、空间向量的加法运算 【问题思考】 1.平面向量加法的三角形法则、平行四边形法则和多边形法 则对于空间向量是否适用? 提示:适用
导航 二、空间向量的加法运算 【问题思考】 1.平面向量加法的三角形法则、平行四边形法则和多边形法 则对于空间向量是否适用? 提示:适用

导航、 2.填空:(1)空间向量的加法运算 已知空间中任意两个向量a,b,在空间中任取一点O,作 OA=a,AB=b,如图所示. B a
导航 2.填空:(1)空间向量的加法运算 已知空间中任意两个向量a,b,在空间中任取一点O,作 𝑶 𝑨 =a,𝑨 𝑩 =b,如图所示
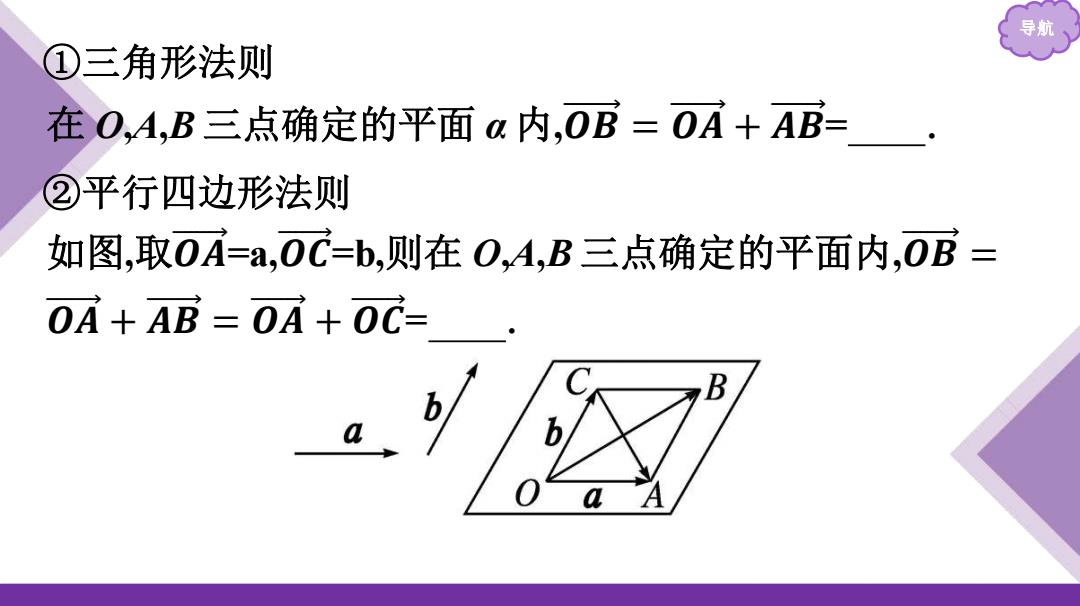
导航 ①三角形法则 在0,A,B三点确定的平面a内,0B=0A+AB= ②平行四边形法则 如图,取0A=a,0C=b,则在O,A,B三点确定的平面内,0B= OA+AB=0A+OC= B
导航 ①三角形法 则 在 O,A,B 三点确定的平面 α 内,𝑶 𝑩 = 𝑶 𝑨 + 𝑨 𝑩 = a + b . ②平行四边形法 则 如图,取 𝑶 𝑨 =a, 𝑶 𝑪 =b,则在 O,A,B 三点确定的平面内,𝑶 𝑩 = 𝑶 𝑨 + 𝑨 𝑩 = 𝑶 𝑨 + 𝑶 𝑪 = a + b