
全程设计 第一章 空间向量与立体几何 1.2 空间向量在立体几何中的应用 1.2.3直线与平面的夹角
第一章 空间向量与立体几何 1.2 空间向量在立体几何中的应用 1.2.3 直线与平面的夹角
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解直线与平面所成角的定义及性质, 2.能够使用空间向量求直线与平面的夹角. 3.加强直观想象和数学运算能力的培养
导航 课标定位素养阐释 1.了解直线与平面所成角的定义及性质. 2.能够使用空间向量求直线与平面的夹角. 3.加强直观想象和数学运算能力的培养

导航 课前·基础认知 直线与平面的夹角 【问题思考】 1.若直线l是平面a的一条斜线,l在平面a内的射影为l',直线a是 平面α内一条直线,设直线与'所成角为0,直线与所成角为 02,请问01,02的大小关系是什么? 提示:01≤02
导航 课前·基础认知 一、直线与平面的夹角 【问题思考】 1.若直线l是平面α的一条斜线,l在平面α内的射影为l',直线a是 平面α内一条直线,设直线l与l'所成角为θ1 ,直线l与a所成角为 θ2 ,请问θ1 ,θ2的大小关系是什么? 提示:θ1≤θ2

导 2,填空:(1)直线与平面的夹角 ①如果一条直线与一个平面垂直,则称这条直线与这个平面 所成的角为 ②如果一条直线与一个平面平行,或直线在平面内,则称这条 直线与这个平面所成的角为 ③平面的斜线与它在平面内的 所成的锐角,称为这条斜 线与平面所成的角. ④直线与平面的夹角的范围是
导航 2.填空:(1)直线与平面的夹角 ①如果一条直线与一个平面垂直,则称这条直线与这个平面 所成的角为 90° . ②如果一条直线与一个平面平行,或直线在平面内,则称这条 直线与这个平面所成的角为 0° . ③平面的斜线与它在平面内的射影所成的锐角,称为这条斜 线与平面所成的角. ④直线与平面的夹角的范围是 𝟎, 𝛑 𝟐
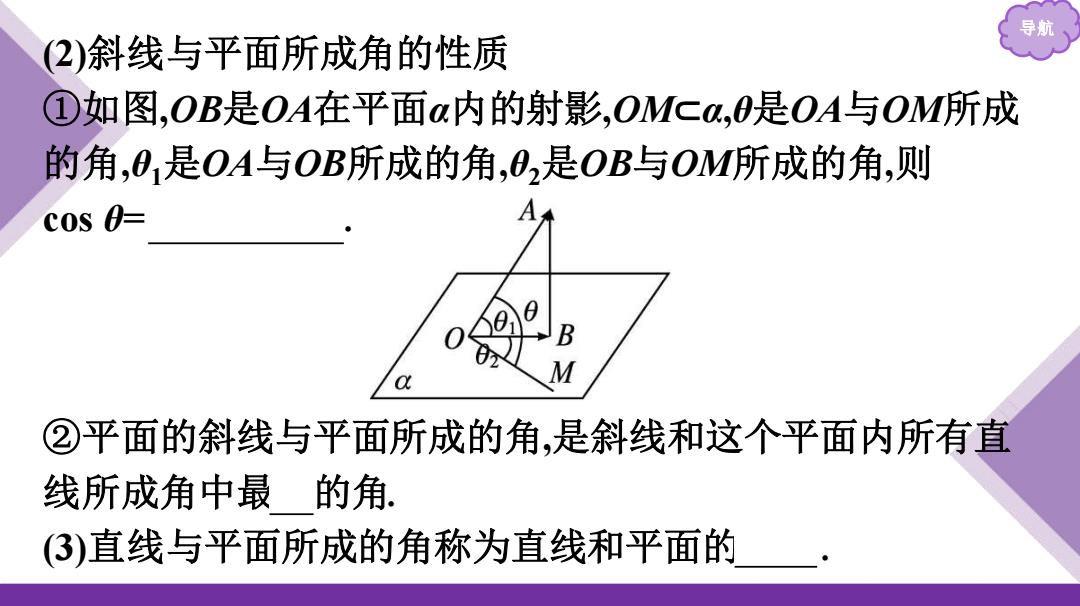
2)斜线与平面所成角的性质 ①如图,OB是OA在平面a内的射影,OMca,0是OA与OM所成 的角,01是OA与OB所成的角,02是OB与OM所成的角,则 cos 0= ②平面的斜线与平面所成的角,是斜线和这个平面内所有直 线所成角中最的角. 3)直线与平面所成的角称为直线和平面的
导航 (2)斜线与平面所成角的性质 ①如图,OB是OA在平面α内的射影,OM⊂α,θ是OA与OM所成 的角,θ1是OA与OB所成的角,θ2是OB与OM所成的角,则 cos θ= cos θ1 cos θ2 . ②平面的斜线与平面所成的角,是斜线和这个平面内所有直 线所成角中最小的角. (3)直线与平面所成的角称为直线和平面的夹角

导航 3.做一做:在正方体ABCD-A1BC1D1中,O为侧面BCC1B1的中 心,则AO与平面ABCD所成角的正弦值为( 3 A. B D
导航 3.做一做:在正方体ABCD-A1B1C1D1中,O为侧面BCC1B1的中 心,则AO与平面ABCD所成角的正弦值为( ) A. 𝟑 𝟑 B.𝟏 𝟐 C. 𝟔 𝟔 D. 𝟑 𝟐

导航 解析:如图,设BC的中点为E,连接AE,OE,易知AE⊥OE,则 ∠OAE就是AO与平面ABCD所成角. D 设正方体的棱长为 在Rt△0AE中,AE=a2+()》 2 a 5 2 40=2+(臣a) 6 D = 2 .0Eza…sin∠0AE- OE = V6 6 答案:C
导航 解析:如图,设BC的中点为E,连接AE,OE,易知AE⊥OE,则 ∠OAE就是AO与平面ABCD所成角. 设正方体的棱长为a. 在 Rt△OAE 中,∵AE= 𝒂𝟐 + 𝒂 𝟐 𝟐 = 𝟓 𝟐 a, AO= 𝒂 𝟐 𝟐 + 𝟓 𝟐 𝒂 𝟐 = 𝟔 𝟐 a, ∴OE=𝟏 𝟐 a.∴sin∠OAE=𝑶𝑬 𝑨𝑶 = 𝟔 𝟔 . 答案:C

导 二、借助直线的方向向量、平面的法向量研究直线与平面所 成角的关系 【问题思考】 1.直线l是平面a的一条斜线,v是的一个方向向量,u是平面a的 一个法向量,和1与a所成的角0有什么关系? 提示:077
导航 二、借助直线的方向向量、平面的法向量研究直线与平面所 成角的关系 【问题思考】 1.直线l是平面α的一条斜线,v是l的一个方向向量,u是平面α的 一个法向量,和l与α所成的角θ有什么关系? 提示:θ= 𝛑 𝟐 -或 θ=- 𝛑 𝟐

导航 2.填空:若v是直线1的一个方向向量,n是平面a的一个法向 量,设直线1与平面a所成角大小为0,则0= .特别地,cos0= ,sin 0=
导航 2.填空:若 v 是直线 l 的一个方向向量,n 是平面 α 的一个法向 量,设直线 l 与平面 α 所成角大小为 θ,则 θ= 𝛑 𝟐 -或 θ=- 𝛑 𝟐 .特别地,cos θ= sin ,sin θ= |cos|