
全程设计 第二章 平面解析几何 2.5 椭圆及其方程 2.5.2 椭圆的几何性质
第二章 平面解析几何 2.5 椭圆及其方程 2.5.2 椭圆的几何性质
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.熟练掌握椭圆的几何性质及简单应用. 2.能利用椭圆的性质解决一些简单问题 3.加强直观想象和数学运算能力的培养
导航 课标定位素养阐释 1.熟练掌握椭圆的几何性质及简单应用. 2.能利用椭圆的性质解决一些简单问题. 3.加强直观想象和数学运算能力的培养

导航 课前·基础认知 椭圆的几何性质 【问题思考】 1.我们知道由曲线的方程可以研究曲线具有的性质.若曲线F 的方程是二+2=1,则曲线F有哪些性质? 提示:(1)x∈[-V2,V2]y∈[-1,1.(2)曲线F关于x轴、y轴、原 点对称.(3)曲线F与坐标轴的交点的坐标为(仕√2,0),(0,±1等
导航 课前·基础认知 椭圆的几何性质 【问题思考】 1.我们知道由曲线的方程可以研究曲线具有的性质.若曲线F 的方程是 +y 2=1,则曲线F有哪些性质? 𝒙 𝟐 𝟐 提示:(1)x∈[- 𝟐, 𝟐],y∈[-1,1].(2)曲线 F 关于 x 轴、y 轴、原 点对称.(3)曲线 F 与坐标轴的交点的坐标为(± 𝟐,0),(0,±1)等
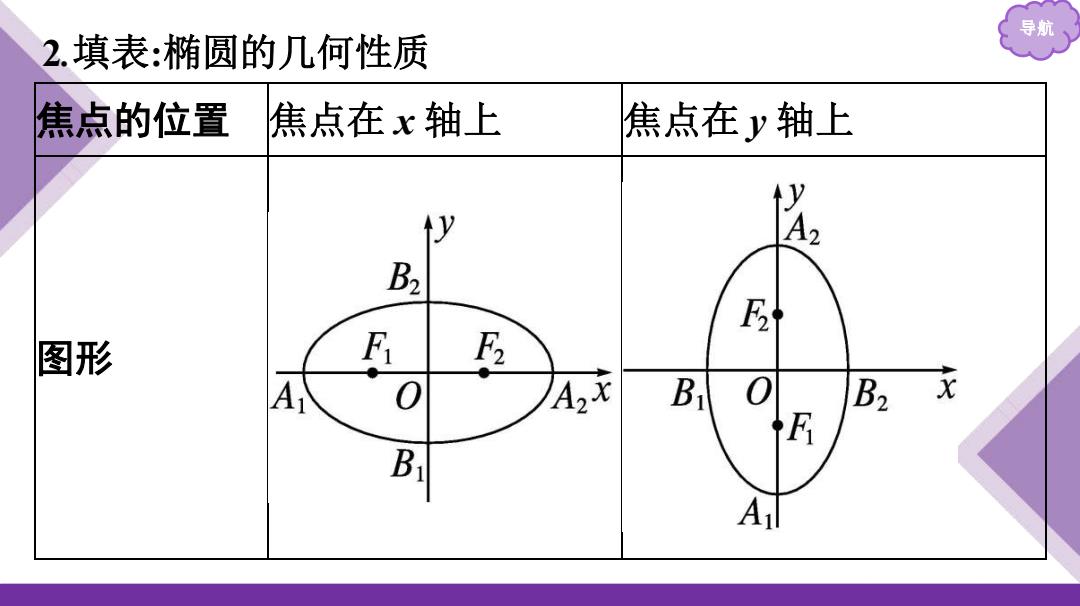
导航 2.填表:椭圆的几何性质 焦点的位置 焦点在x轴上 焦点在y轴上 y 送 B2 F2 卧 图形 A 0 A2x Bi 0 B2 E A
导航 2 .填表 :椭圆的几何性 质 焦点的位置 焦点在 x 轴上 焦点在 y 轴上 图形

导航 焦点的位置 焦点在x轴上 焦点在y轴上 标准方程 ¥+-iab0 范围 ,-b<y<b -bs≤b, A1(-4,0),A2(a,0) A1(0,-),A2(0,0 顶点 B1(-b,0),B2(b,0)
导航 焦点的位置 焦点在 x 轴上 焦点在 y 轴上 标准方程 𝐱 𝟐 𝐚 𝟐 + 𝐲 𝟐 𝐛𝟐 =1(a>b>0) 𝐲 𝟐 𝐚 𝟐 + 𝐱 𝟐 𝐛𝟐 =1(a>b>0) 范围 -a≤x≤a ,-b≤y≤b -b≤x≤b, -a≤y≤a 顶点 A1(-a,0),A2(a,0) B1(0,-b),B2(0,b) A1(0,-a),A2(0,a) B1(-b,0),B2(b,0)

导航 焦点的位置 焦点在x轴上 焦点在y轴上 轴长 长轴长=,短轴长= 焦点 F1(-C,0),F2(C,0) 焦距 2c 对称性 对称轴: ,对称中心: 离心率 (0<e<1)
导航 焦点的位置 焦点在 x 轴上 焦点在 y 轴上 轴长 长轴长= 2a ,短轴长= 2b 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c) 焦距 2c 对称性 对称轴:坐标轴,对称中心:原点(0,0) 离心率 e= 𝐜 𝐚 (0<e<1)

导航 3微一做:椭圆后+若1的焦点坐标是 25 ;焦距 是 ;长轴长为 ;离心率e= 答案:(0,3)610 3-5
导航 3.做一做:椭圆𝒙 𝟐 𝟏𝟔 + 𝒚 𝟐 𝟐𝟓 =1 的焦点坐标是 ;焦距 是 ;长轴长为 ;离心率 e= . 答案:(0,±3) 6 10 𝟑 𝟓

导航 【思考辨析】 判断正误(正确的画“√”,错误的画“义”) 椭圆是轴对称图形() (2)在椭圆中,焦距越大,离心率越大( 3)椭圆号+号1的长销长为3( ④在方程器+兰1a>0中,y的取值范围均为 (-0,+0).(
导航 【思考辨析】 判断正误 . (正确的画 “ ”,错误的画 “ ×”) (1)椭圆是轴对称图形 . ( ) (2)在椭圆中 ,焦距越大 ,离心率越大 .( × ) (3)椭圆 𝒙 𝟐𝟒 + 𝒚 𝟐𝟗 =1 的长轴长为 3.( × ) (4)在方程 𝒙 𝟐 𝒂 𝟐 + 𝒚 𝟐 𝒃 𝟐 =1(a>b>0) 中,x,y 的取值范围均为 (-∞,+∞).( × )

导航、 课堂·重难突破 探究一椭圆的几何性质 【例1】求椭圆9x2+16y2=144的长轴长、短轴长、离心率、 焦点坐标和顶点坐标
导航 课堂·重难突破 探究一 椭圆的几何性质 【例1】求椭圆9x 2+16y 2=144的长轴长、短轴长、离心率、 焦点坐标和顶点坐标