
全程设计 5.2.2 等差数列的前n项和 第1课时 等差数列的前n须和
5.2.2 等差数列的前n项和 第1课时 等差数列的前n项和
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 L.理解等差数列前项和公式的推导方法一倒序相加法, 2.掌握等差数列前n项和公式,掌握等差数列五个量 a1,n,d,amSn之间的关系. 3.掌握由Sn求Ln的方法 4.提高逻辑推理、数学运算和数学抽象的能力
导航 课标定位素养阐释 1.理解等差数列前n项和公式的推导方法——倒序相加法. 2.掌握等差数列前n项和公式,掌握等差数列五个量 a1 ,n,d,an ,Sn之间的关系. 3.掌握由Sn求an的方法. 4.提高逻辑推理、数学运算和数学抽象的能力

导航 课前·基础认知 等差数列的前n项和 【问题思考】 1.如图,建筑工地上堆放着一些钢管,最上面的一层有4根,下面 的每一层都比上一层多一根,共6层在不逐个相加的情况下, 你能想办法算出这些钢管共有多少根吗?
导航 课前·基础认知 等差数列的前n项和 【问题思考】 1.如图,建筑工地上堆放着一些钢管,最上面的一层有4根,下面 的每一层都比上一层多一根,共6层.在不逐个相加的情况下, 你能想办法算出这些钢管共有多少根吗?
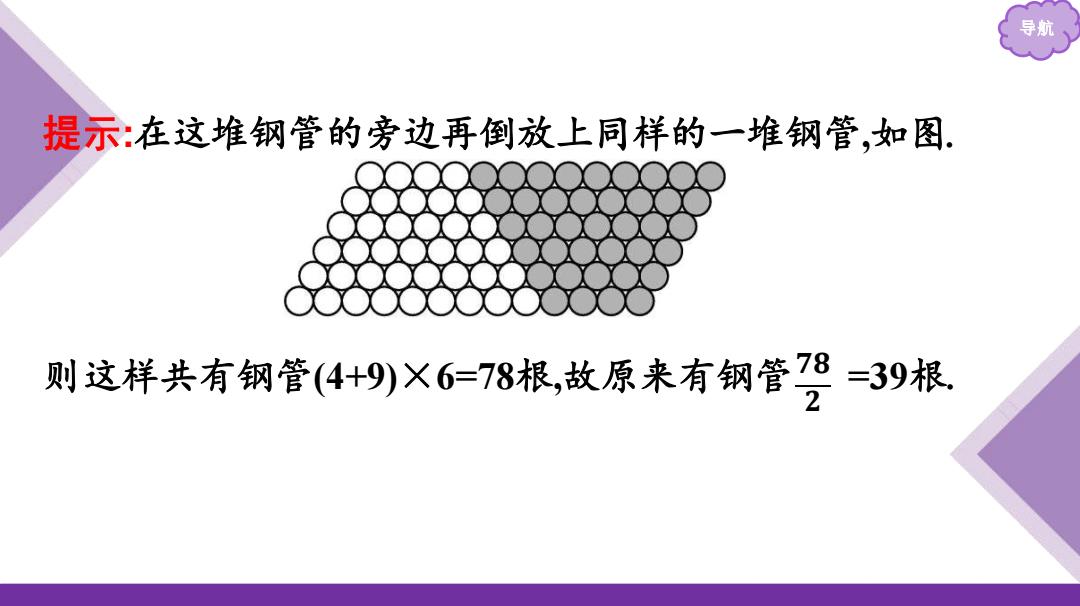
导航 提示:在这堆钢管的旁边再倒放上同样的一堆钢管,如图 则这样共有钢管(4+9)×6=78根,故原来有钢管7=39根
导航 提示:在这堆钢管的旁边再倒放上同样的一堆钢管,如图. 则这样共有钢管(4+9)×6=78根,故原来有钢管 =39根. 𝟕𝟖 𝟐

2.你知道高斯求和的故事吗?请同学们交流一下,高斯是怎样 求1+2+3+…+100的结果的? 提示:对于这个问题,著名数学家高斯的思路和解答方法是 S=1+2+3+…+99+100, 把加数倒序写一遍S=100+99+98++2+1. 所以有2S=(1+100)+(2+99)++(99+2)+(100+1)=100×101, 所以S=50×101=5050
导航 2.你知道高斯求和的故事吗?请同学们交流一下,高斯是怎样 求1+2+3+…+100的结果的? 提示:对于这个问题,著名数学家高斯的思路和解答方法是 S=1+2+3+…+99+100, 把加数倒序写一遍S=100+99+98+…+2+1. 所以有2S=(1+100)+(2+99)+…+(99+2)+(100+1)=100×101, 所以S=50×101=5 050

导 3.你能借鉴上面两个问题中的计算方法推导出一般等差数列 {a,}的前n项和公式吗? 提示:Sm=a1+2+3++m-l+0w Sm=n+0n-1tan-2+…+2+01, ..2S,-(atan)Xn, .S matan 2
导航 3.你能借鉴上面两个问题中的计算方法推导出一般等差数列 {an }的前n项和公式吗? 提示:∵Sn=a1+a2+a3+…+an-1+an , Sn=an+an-1+an-2+…+a2+a1 , ∴2Sn =(a1+an )×n, ∴Sn = 𝒏(𝒂𝟏 +𝒂𝒏) 𝟐

导航 4.你能将等差数列{a}的前n项和公式用其首项a1,公差d,项数 n表达出来吗? 提示:S=na1t2(Un-l)M
导航 4.你能将等差数列{an }的前n项和公式用其首项a1 ,公差d,项数 n表达出来吗? 提示:Sn=na1+ 𝟏 𝟐 n(n-1)d

导航 5.填空:等差数列前项和公式的推导方法为“倒序相加法,等 差数列的前n项和公式如下表所示. 已知量 首项、末项与项数 首项、公差与项数 求和公式 S= (ai+an) 2 Sn=
导航 5.填空:等差数列前n项和公式的推导方法为“倒序相加法”,等 差数列的前n项和公式如下表所示. 已知量 首项、末项与项数 首项、公差与项数 求和公式 Sn= 𝐧(𝐚𝟏 +𝐚𝐧) 𝟐 Sn=na1+ 𝐧(𝐧-𝟏) 𝟐 d

导 6.做一做:(1)已知数列{a}的通项公式m=n2+1,若其前n项和 为Sm则S3= (2)已知数列{a}为等差数列,首项a1=2,公差d=2,则其前n项和 S (3)已知数列{a}为等差数列,1=2,4,=10Sm=72,则 n= 答案:1)17 (2)n2+n (3)12
导航 6.做一做:(1)已知数列{an }的通项公式an=n2+1,若其前n项和 为Sn ,则S3 = . (2)已知数列{an }为等差数列,首项a1 =2,公差d=2,则其前n项和 Sn = . (3)已知数列{an }为等差数列,a1 =2,an =10,Sn =72,则 n= . 答案:(1)17 (2)n 2+n (3)12