
全程设计 6.1.1 数的平均变化率
6.1.1 函数的平均变化率
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导 课标定位素养阐释 1理解函数平均变化率的含义,会求函数在区间上的平均变化 率 2.领会以直代曲的方法. 3.会求位移函数在某段时间内的平均速度,理解平均变化率的 物理意义 4通过对平均变化率的理解与运用,提高数学抽象、直观想象 与数学运算的核心素养
导航 课标定位素养阐释 1.理解函数平均变化率的含义,会求函数在区间上的平均变化 率. 2.领会以直代曲的方法. 3.会求位移函数在某段时间内的平均速度,理解平均变化率的 物理意义. 4.通过对平均变化率的理解与运用,提高数学抽象、直观想象 与数学运算的核心素养
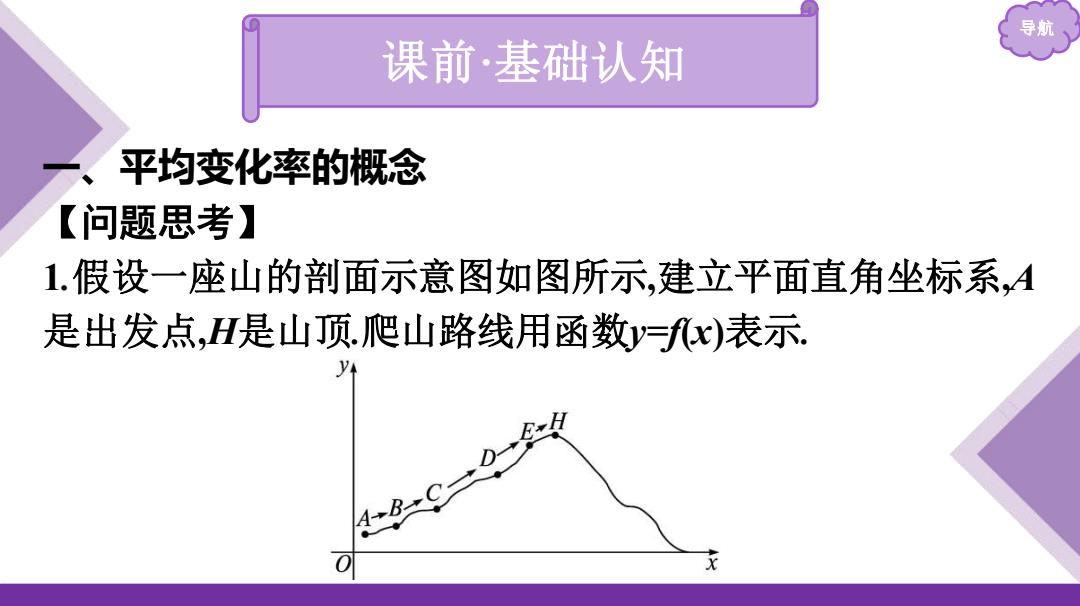
导航 课前·基础认知 一、平均变化率的概念 【问题思考】 1.假设一座山的剖面示意图如图所示建立平面直角坐标系,A 是出发点,H是山顶爬山路线用函数y=x)表示
导航 课前·基础认知 一、平均变化率的概念 【问题思考】 1.假设一座山的剖面示意图如图所示,建立平面直角坐标系,A 是出发点,H是山顶.爬山路线用函数y=f(x)表示

自变量x表示某旅游者的水平位置,函数值y=fx)表示此时旅 游者所在的高度.设点A的坐标为化1y),点B的坐标为(c2y2). ()若旅游者从点A爬到点B,自变量x和函数值y的改变量分别 是多少? 提示:自变量x的改变量为xx,记作△K,函数值的改变量为y2 y1,记作△ (2)根据y的改变量的大小能否判断山路的陡峭程度? 提示:不能.山路的陡峭程度也与自变量x的改变量有关
导航 自变量x表示某旅游者的水平位置,函数值y=f(x)表示此时旅 游者所在的高度.设点A的坐标为(x1 ,y1 ),点B的坐标为(x2 ,y2 ). (1)若旅游者从点A爬到点B,自变量x和函数值y的改变量分别 是多少? 提示:自变量x的改变量为x2 -x1 ,记作Δx,函数值的改变量为y2 - y1 ,记作Δy. (2)根据y的改变量的大小能否判断山路的陡峭程度? 提示:不能.山路的陡峭程度也与自变量x的改变量有关

导航 3)怎样用数量刻画弯曲山路AB的陡峭程度? 提示:对于山路AB,可用 Ay=y2y1 近似地刻画其陡峭程度, X2-X1
导航 (3)怎样用数量刻画弯曲山路AB的陡峭程度? 提示:对于山路AB,可用 近似地刻画其陡峭程度. 𝚫𝒚 𝚫𝒙 = 𝒚𝟐 -𝒚𝟏 𝒙𝟐-𝒙𝟏

2.填空:一般地,若函数y=fx)的定义域为D,且 X12∈D,x12y1fK1)y2f2),则称△=x2x1为 的改 变量;称△y=yy(或Ax2)x)为相应的 的改变量; 称 为函数y=fx)在以1,x2为端 点的闭区间上的平均变化率.由于x2=1+x,而且 2fc1+Ax),因此平均变化率上=fx1+△fx △X (x1+△x)-x1 f(x1+△x)-f(x1) △x
导航 2.填空:一般地,若函数y=f(x)的定义域为D,且 x1 ,x2∈D,x1≠x2 ,y1=f(x1 ),y2=f(x2 ),则称Δx=x2 -x1为自变量 的改 变量;称Δy=y2 -y1 (或Δf=f(x2 )-f(x1 ))为相应的 因变量 的改变量; 称 𝚫𝒚 𝚫𝒙 = 𝒚𝟐 -𝒚𝟏 𝒙𝟐-𝒙𝟏 (或 𝚫𝒇 𝚫𝒙 = 𝒇(𝒙𝟐)-𝒇(𝒙𝟏) 𝒙𝟐-𝒙𝟏 )为函数 y=f(x)在以 x1,x2为端 点的闭区间上的平均变化率.由于 x2=x1+Δx,而且 f(x2)=f(x1+Δx),因此平均变化率𝚫𝒇 𝚫𝒙 = 𝒇(𝒙𝟏 +𝚫𝒙)-𝒇(𝒙𝟏) (𝒙𝟏 +𝚫𝒙)-𝒙𝟏 = 𝒇(𝒙𝟏 +𝚫𝒙)-𝒇(𝒙𝟏) 𝚫𝒙

导航、 3.△x的取值一定是正值吗? 提示:不一定.x可以为正,也可以为负. 4.公式中,若将△x改为x1x2,则△是否还是fx2)fx)? 提示:若△x=x2x1,则△ffx2)x1);若△x=x1x2,则△Fx1)fx2)
导航 3.Δx的取值一定是正值吗? 提示:不一定.Δx可以为正,也可以为负. 4.公式中,若将Δx改为x1 -x2 ,则Δf是否还是f(x2 )-f(x1 )? 提示:若Δx=x2 -x1 ,则Δf=f(x2 )-f(x1 );若Δx=x1 -x2 ,则Δf=f(x1 )-f(x2 )

导 5.做一做:已知函数f孔x)=2x+1,则函数fx)在以x和xo+x为端 点的闭区间上的平均变化率为( A.-2 B.2 C.3 D.不确定 答案:B 解析:fxo+△x)f孔x0)=2Ko+x)+1-2x-1=2△,故平均变化率为 fxo+△x)-fxo= 2Ax=2. △X △X
导航 5.做一做:已知函数f(x)=2x+1,则函数f(x)在以x0和x0+Δx为端 点的闭区间上的平均变化率为( ) A.-2 B.2 C.3 D.不确定 答案:B 解析:f(x0+Δx)-f(x0 )=2(x0+Δx)+1-2x0 -1=2Δx,故平均变化率为 𝒇(𝒙𝟎 +𝚫𝒙)-𝒇(𝒙𝟎) 𝚫𝒙 = 𝟐𝚫𝒙 𝚫𝒙 =2
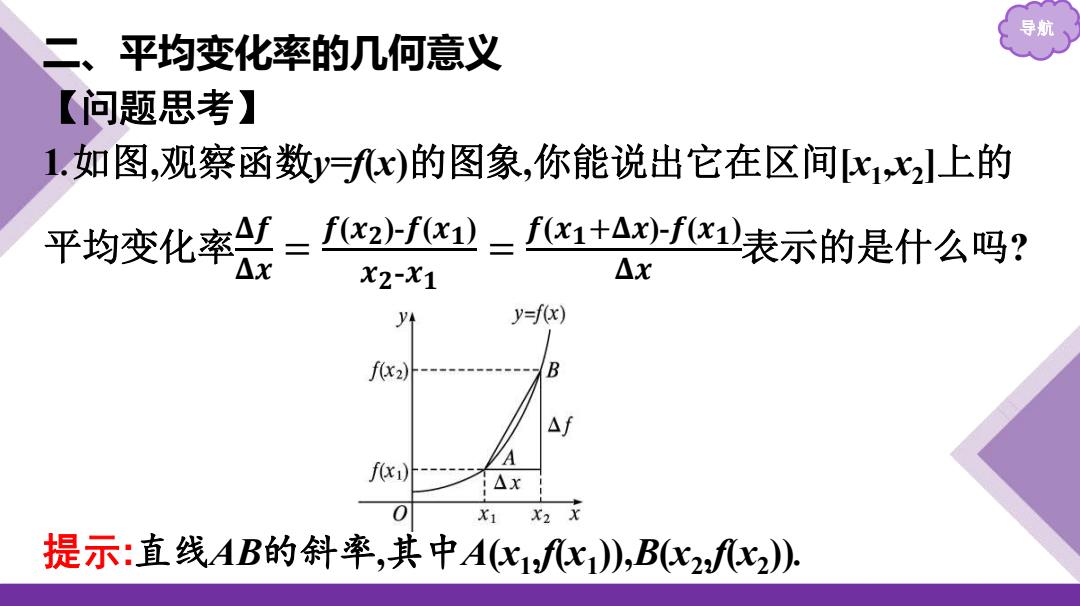
导期 二、平均变化率的几何意义 【问题思考】 1.如图,观察函数y=x)的图象,你能说出它在区间K1心上的 平均变化率g=f2少f)-1+Axf表示的是什么吗? △X X2-X1 △X y y=f(x) f(x2)-- B Af f(x) △x X1 X2 X 提示:直线AB的斜率,其中A(c11),B(心22)
导航 二、平均变化率的几何意义 【问题思考】 1.如图,观察函数y=f(x)的图象,你能说出它在区间[x1 ,x2 ]上的 平均变化率𝚫𝒇 𝚫𝒙 = 𝒇(𝒙𝟐)-𝒇(𝒙𝟏) 𝒙𝟐-𝒙𝟏 = 𝒇(𝒙𝟏 +𝚫𝒙)-𝒇(𝒙𝟏) 𝚫𝒙 表示的是什么吗? 提示:直线AB的斜率,其中A(x1 ,f(x1 )),B(x2 ,f(x2 ))