
全程设计 复习课 第2课时 概率与统计
复习课 第2课时 概率与统计

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破
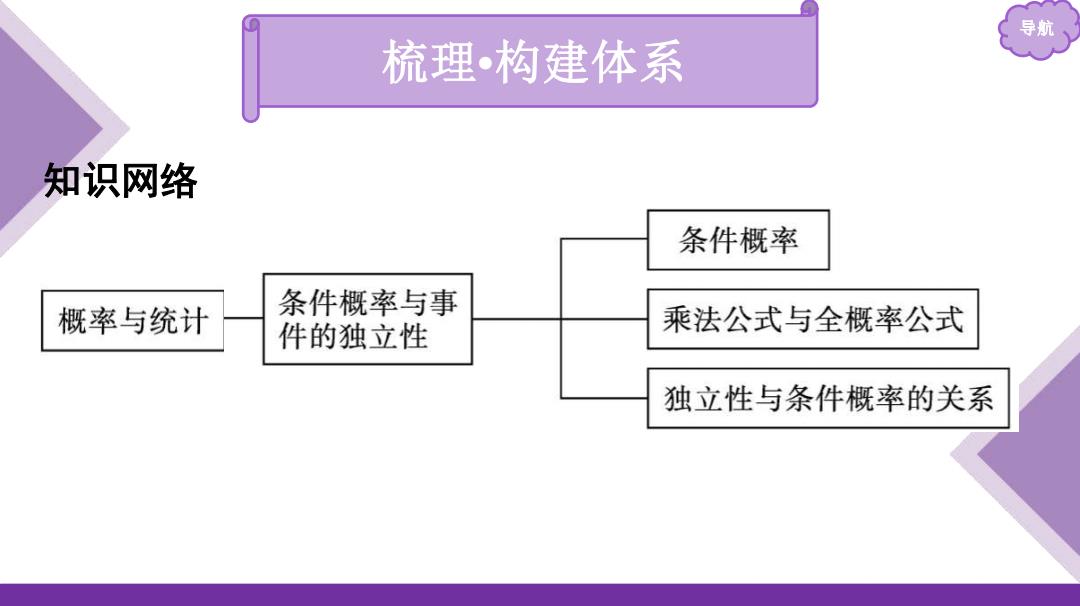
导航 梳理构建体系 知识网络 条件概率 概率与统计 条件概率与事 件的独立性 乘法公式与全概率公式 独立性与条件概率的关系
导航 梳理 •构建体系 知识网 络
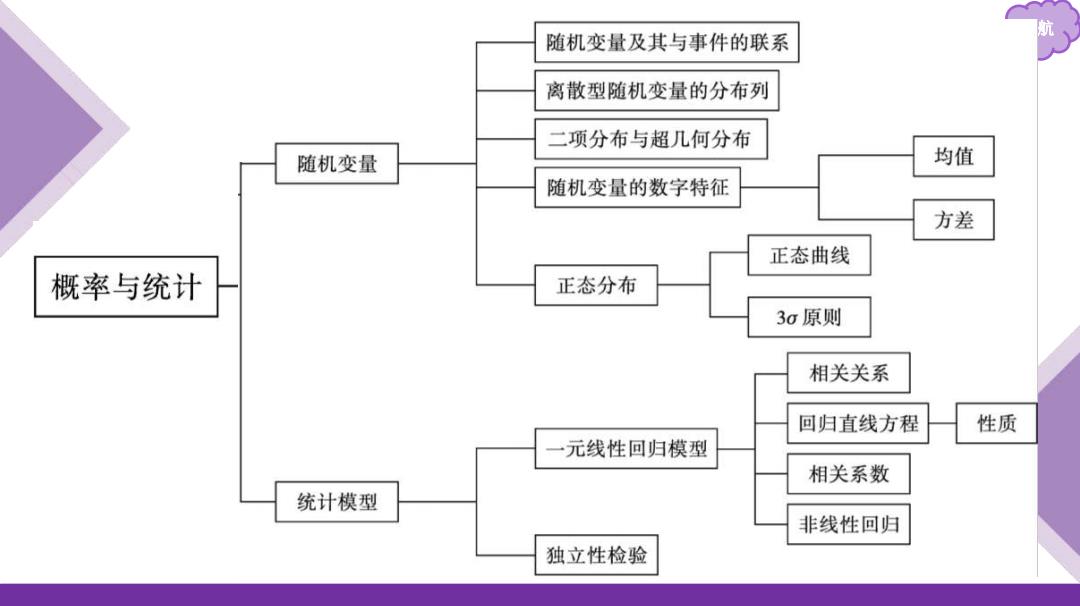
随机变量及其与事件的联系 离散型随机变量的分布列 二项分布与超几何分布 随机变量 均值 随机变量的数字特征 方差 正态曲线 概率与统计 正态分布 30原则 相关关系 回归直线方程 性质 元线性回归模型 相关系数 统计模型 非线性回归 独立性检验
导航

导期 要点梳理 1.条件概率的概念是什么?具有什么性质? 提示:(1)一般地,当事件B发生的概率大于0时(即P(B)>0),已知 事件B发生的条件下事件A发生的概率,称为条件概率,记作 P4B,而且PAB)=PAn8 P(B) (2)假设A,B,C都是事件,且P(A>0,根据条件概率的定义,可得 ①0≤P(BA)1;②P(AA)=1;③如果B与C互斥,则 P((BUC)A)=P(BA)+P(CA)
导航 要点梳理 1.条件概率的概念是什么?具有什么性质? 提示:(1)一般地,当事件B发生的概率大于0时(即P(B)>0),已知 事件B发生的条件下事件A发生的概率,称为条件概率,记作 P(A|B),而且P(A|B) = (2)假设A,B,C都是事件,且P(A)>0,根据条件概率的定义,可得 ①0≤P(B|A)≤1;②P(A|A) =1;③如果B与C互斥,则 P((B∪C)|A)=P(B|A)+P(C|A). 𝑷(𝑨⋂𝑩) 𝑷(𝑩)

导航 2.乘法公式与全概率公式是什么? 提示:(山由条件概率的计算公式P(BA) PBA可知,PBA)=PA) P(A) P(BA),这就是说,根据事件A发生的概率,以及已知事件A发生 的条件下事件B发生的概率,可以求出A与B同时发生的概率 一般地,这个结论称为乘法公式
导航 2.乘法公式与全概率公式是什么? 提示:(1)由条件概率的计算公式 可知,P(BA)=P(A) P(B|A),这就是说,根据事件A发生的概率,以及已知事件A发生 的条件下事件B发生的概率,可以求出A与B同时发生的概率. 一般地,这个结论称为乘法公式. P(B|A)= 𝑷(𝑩𝑨) 𝑷(𝑨)

(2)一般地,如果样本空间为2,而A,B为事件,则BA与BA是互 斥的,且B=B2=B(A+A=BA+BA,从而 P(B)=P(A)P(BA)+P(A)P(BA).这称为全概率公式. 若样本空间2中的事件A1,A2,,An满足: ①任意两个事件均互斥,即A=⑦,i=1,2,,n,j; ②A1+A2+..+Am=2; ③P(A)>0,i=1,2,…,n. 则对2中的任意事件B,都有B=BA1+BA2+..+BA, 且P(B)=∑P(BA)=∑PA)P(BA.上述公式也称为全概率公式 i=1 =1
导航 (2)一般地,如果样本空间为 Ω,而 A,B 为事件,则 BA 与 B𝑨是互 斥的,且 B=BΩ=B(A+𝑨)=BA+B𝑨,从而 P(B)=P(A)P(B|A)+P(𝑨)P(B|𝑨).这称为全概率公式. 若样本空间 Ω 中的事件 A1,A2,…,An满足: ①任意两个事件均互斥,即 AiAj=⌀,i,j=1,2,…,n,i≠j; ②A1+A2+…+An=Ω; ③P(Ai)>0,i=1,2,…,n. 则对 Ω 中的任意事件 B,都有 B=BA1+BA2+…+BAn, 且 P(B)= ∑ 𝒊=𝟏 𝒏 P(BAi)= ∑ 𝐢=𝟏 𝐧 P(Ai)P(B|Ai).上述公式也称为全概率公式

3.离散型随机变量的分布列是什么?它有什么性质? 提示:()分布列的定义:一般地,当离散型随机变量X的取值范 围是{化1,水2,,比n}时,如果对任意k∈{1,2,,m,概率PX=x=P 都是已知的,则称X的概率分布是已知的.离散型随机变量X的 概率分布可以用如下形式的表格表示,这个表格称为X的概率 分布或分布列. X xL X2 Xk ●●e Xn P P2 。… Pk (2)分布列的性质 n ①p20,k=l,2,n②④p1tp2+.t忆m=1
导航 3.离散型随机变量的分布列是什么?它有什么性质? 提示:(1)分布列的定义:一般地,当离散型随机变量X的取值范 围是{x1 ,x2 ,…,xn }时,如果对任意k∈{1,2,…,n},概率P(X=xk )=pk 都是已知的,则称X的概率分布是已知的.离散型随机变量X的 概率分布可以用如下形式的表格表示,这个表格称为X的概率 分布或分布列. X x1 x2 … xk … xn P p1 p2 … pk … pn (2)分布列的性质 ①pk≥0,k=1,2,…,n;② ∑ pk=p1+p2+…+pn =1. 𝒌=𝟏 𝒏

导 4.什么是二项分布? 提示:一般地,如果一次伯努利试验中,出现“成功”的概率为p, 记q=1-p,且n次独立重复试验中出现“成功”的次数为X,则X的 取值范围是{0,1,…,k,…,, 而且PX=k)=Ckpq-k,k=0,1,,n, 因此X的分布列如下表所示 X o k n P Cop'g" Cnp g"-1 ..Cpfgk Cnp"go
导航 4.什么是二项分布? 提示:一般地,如果一次伯努利试验中,出现“成功”的概率为p, 记q=1-p,且n次独立重复试验中出现“成功”的次数为X,则X的 取值范围是{0,1,…,k,…,n}, 而且P(X=k)= pkq n-k ,k=0,1,…,n, 因此X的分布列如下表所示. X 0 1 … k … n P 𝑪𝐧 𝟎 p 0 q n 𝑪𝐧 𝟏 p 1 q n-1 … 𝑪𝐧 𝐤 p k q n-k … 𝑪𝐧 𝐧 p n q 0 𝐂𝒏 𝒌

导航 注意到上述X的分布列第二行中的概率值都是二项展开式 (q+p)"=CDq"+Chq-1+..+Cq-k+.+Cp”q中对应项的 值,因此称X服从参数为n,p的二项分布,记作X~B(np)
导航 注意到上述 X 的分布列第二行中的概率值都是二项展开式 (q+p) n =𝐂𝒏 𝟎 p 0 q n +𝐂𝒏 𝟏 p 1 q n-1 +…+𝐂𝒏 𝒌 p k q n-k +…+𝐂𝒏 𝒏 p n q 0 中对应项的 值,因此称 X 服从参数为 n,p 的二项分布,记作 X~B(n,p)