
全程设计 第四章 概率与统计 4.2 随机变量 4.2.5 正态分布
第四章 概率与统计 4.2 随机变量 4.2.5 正态分布
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位 素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.理解正态曲线的概念及性质. 2.理解正态分布的均值、方差及其含义, 3.了解3σ原则,会用正态分布解决实际问题 4体会正态曲线、正态分布的发现过程,加强数学抽象和数据 分析能力的培养
导航 课标定位 素养阐释 1.理解正态曲线的概念及性质. 2.理解正态分布的均值、方差及其含义. 3.了解3σ原则,会用正态分布解决实际问题. 4.体会正态曲线、正态分布的发现过程,加强数学抽象和数据 分析能力的培养
导航 课前·基础认知 正态分布 【问题思考】 2 L函数f (x-四) e22,x∈R的图象如图所示. 1 ty 10J2元 72 X
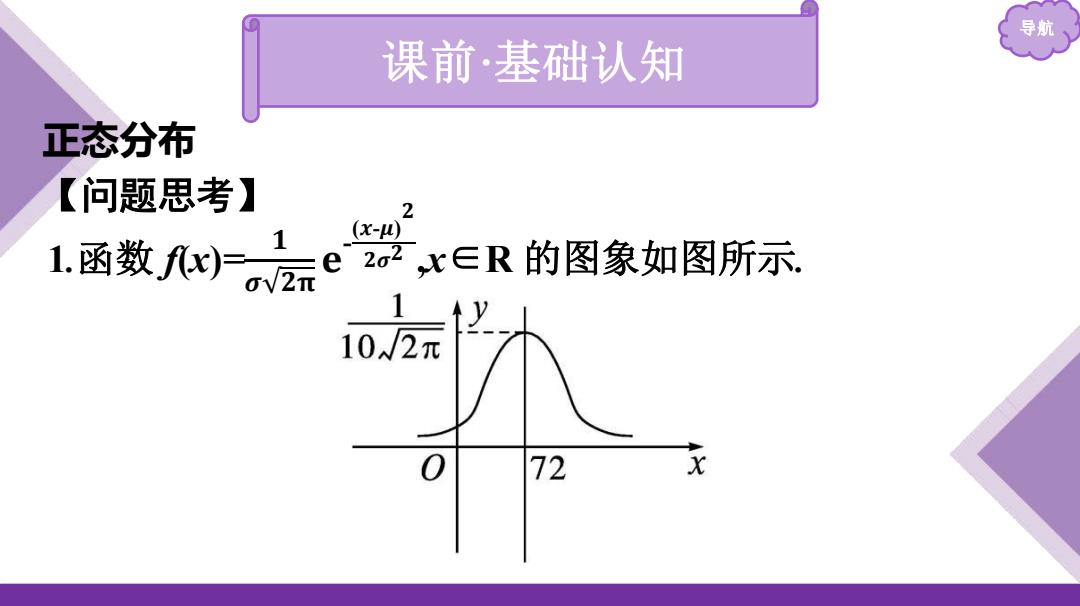
导航 课前 ·基础认知 正态分布 【问题思考】 1.函数 f(x)= 𝟏 𝝈 𝟐𝛑 𝐞-(𝒙-𝝁)𝟐 𝟐𝝈𝟐 ,x∈R 的图象如图所示

导 )由图可以得到函数x)的图象关于哪条直线对称? 提示:直线x=72. (2)当函数fx)取得最大值时x的值是什么?由此可以得到的 值是什么? 提示:x=72,=72. (3)由以上的讨论得到函数fx)的解析式是什么? 2 (x-72) 提示oze c∈R)
导航 (1)由图可以得到函数f(x)的图象关于哪条直线对称? 提示:直线x=72. (2)当函数f(x)取得最大值时,x的值是什么?由此可以得到μ的 值是什么? 提示:x=72,μ=72. (3)由以上的讨论得到函数f(x)的解析式是什么? 提示:f(x)= 𝟏 𝟏𝟎 𝟐𝛑 𝐞 - (𝒙-𝟕𝟐) 𝟐 𝟐𝟎𝟎 (x∈R)
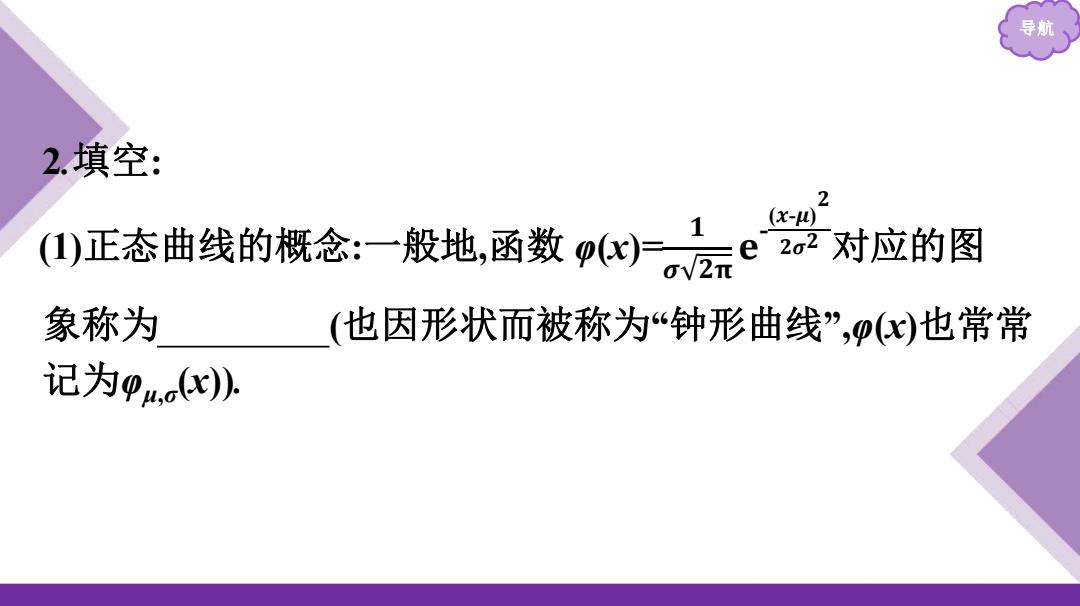
导航 2.填空: 2 山正态曲线的橱念:一股地,函数)、” =e22 对应的图 象称为 (也因形状而被称为“钟形曲线”,p(x)也常常 记为pu.ax)
导航 2.填空: 象称为 正态曲线 (也因形状而被称为“钟形曲线”,φ(x)也常常 记为φμ,σ (x)). (1)正态曲线的概念:一般地,函数 φ(x)= 𝟏 𝝈 𝟐𝛑 𝐞 - (𝒙-𝝁) 𝟐 𝟐𝝈𝟐 对应的图

导加 (2)正态曲线的性质: ①正态曲线关于 对称(即决定正态曲线对称轴的位置), 具有中间高、两边低的特点; ②正态曲线与x轴所围成的图形面积为; ③σ决定正态曲线的“胖瘦:σ ,说明标准差越大,数据的 集中程度越弱,所以曲线越“胖”,σ,说明标准差越小,数据 的集中程度越强,所以曲线越“瘦
导航 (2)正态曲线的性质: ①正态曲线关于 x=μ 对称(即 μ 决定正态曲线对称轴的位置), 具有中间高、两边低的特点; ②正态曲线与x轴所围成的图形面积为1 ; ③σ决定正态曲线的“胖瘦”:σ 越大 ,说明标准差越大,数据的 集中程度越弱,所以曲线越“胖”,σ 越小 ,说明标准差越小,数据 的集中程度越强,所以曲线越“瘦”

导航 3)正态分布的概念:一般地,如果随机变量X落在区间α,b1内 的概率,总是等于pux)对应的正态曲线与x轴在区间[a,b]内 围成的面积,则称X服从参数为μ与c的正态分布,记作 ,此时p,o(x)称为X的概率密度函数此时u是X的均 值,而σ是X的标准差,是X的方差
导航 (3)正态分布的概念:一般地,如果随机变量X落在区间[a,b]内 的概率,总是等于φμ,σ (x)对应的正态曲线与x轴在区间[a,b]内 围成的面积,则称X服从参数为μ与σ的正态分布,记作 X~N(μ,σ 2 ) ,此时φμ,σ (x)称为X的概率密度函数.此时μ是X的均 值,而σ是X的标准差, σ 2 是X的方差

导航 (43o”原则:如果X~N(,62),那么 P(X<u)=P(X=u)= P(K-o)=P(-o≤XKu+o≈ P(X-2o)=P(-2osX≤+2o)≈ P(X-3o)=P(u-3osX≤u+3σ)≈ 最后的式子意味着X约有 的可能会落在距均值3个标 准差的范围之内,也就是说只有约0.3%的可能会落入这一范 围之外(这样的事件可看成小概率事件),这一结论通常称为正 态分布的“3σ原则
导航 (4)“3σ”原则:如果X~N(μ,σ 2 ),那么 P(X≤μ)=P(X≥μ)= 50% ; P(|X-μ|≤σ)=P(μ-σ≤X≤μ+σ)≈ 68.3% ; P(|X-μ|≤2σ)=P(μ-2σ≤X≤μ+2σ) ≈ 95.4% ; P(|X-μ|≤3σ)=P(μ-3σ≤X≤μ+3σ) ≈ 99.7% . 最后的式子意味着,X约有99.7% 的可能会落在距均值3个标 准差的范围之内,也就是说只有约0.3%的可能会落入这一范 围之外(这样的事件可看成小概率事件),这一结论通常称为正 态分布的“3σ原则”

导航 (⑤)标准正态分布:=0且=1的正态分布称为标准正态分布.如 果X~N(0,1),那么对于任意a,通常记()=PX<,也就是说 Φ()表示N(0,1)对应的正态曲线与x轴在区间(-oo,)内所围的 面积
导航 (5)标准正态分布:μ=0且σ=1的正态分布称为标准正态分布.如 果 X~N(0,1),那么对于任意a,通常记Φ(a)=P(X<a),也就是说 Φ(a)表示N(0,1)对应的正态曲线与x轴在区间(-∞,a)内所围的 面积