
全程设计 第四章 概率与统计 4.3 统计模型 4.3.2 独立性检验
第四章 概率与统计 4.3 统计模型 4.3.2 独立性检验
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位 素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.通过实例,理解2×2列联表的统计意义, 2.通过实例,理解独立性检验及其应用. 3.体会数学抽象的过程,加强数学建模和数学运算能力的培养
导航 课标定位 素养阐释 1.通过实例,理解2×2列联表的统计意义. 2.通过实例,理解独立性检验及其应用. 3.体会数学抽象的过程,加强数学建模和数学运算能力的培养
导 课前·基础认知 独立性检验 【问题思考】 1某省教育厅大力推行素质教育,增加了高中生的课外活动时 间,某校调查了学生的课外活动方式,结果如下表 性别 课外活动 体育 文娱 总计 男生 210 230 440 女生 60 290 350 总计 270 520 790
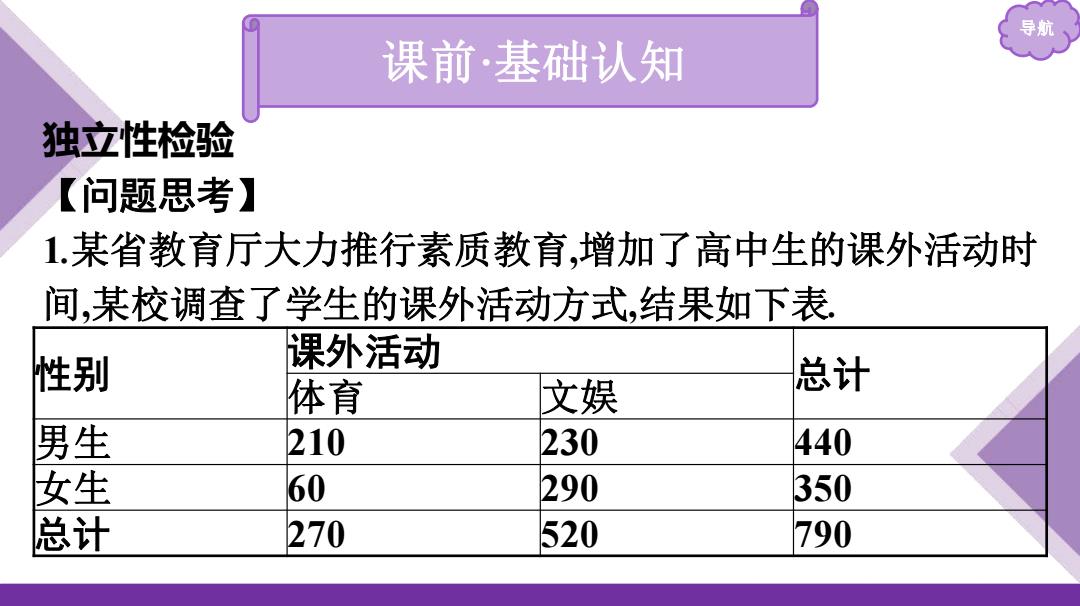
导航 课前·基础认知 独立性检验 【问题思考】 1.某省教育厅大力推行素质教育,增加了高中生的课外活动时 间,某校调查了学生的课外活动方式,结果如下表. 性别 课外活动 总计 体育 文娱 男生 210 230 440 女生 60 290 350 总计 270 520 790

导航 如何判定“喜欢体育还是文娱与性别是否有联系”? 提示:可通过表格与图形进行直观分析,也可通过统计分析定 量判断
导航 如何判定“喜欢体育还是文娱与性别是否有联系”? 提示:可通过表格与图形进行直观分析,也可通过统计分析定 量判断
导航 2填空: (1)如果随机事件A与B的样本数据的2×2列联表如下. A A 总计 B L b a+b B c d c+d 总计 a+c b+d a+b+c+d 2 i记n=a+btc+l.设X-e9eo+ n(ad-bc
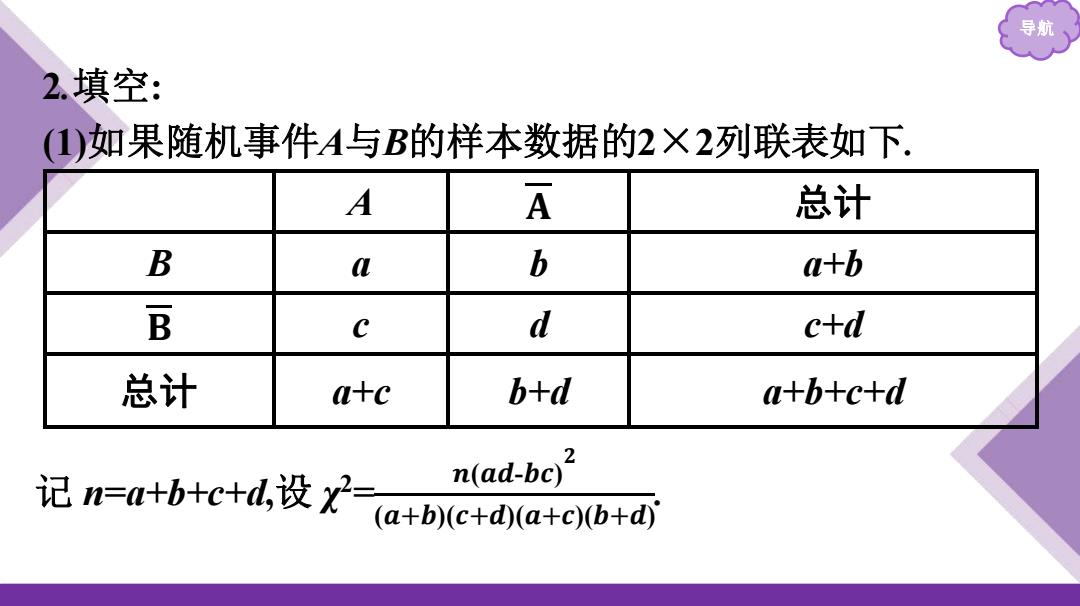
导航 2.填空: (1)如果随机事件A与B的样本数据的2×2列联表如下. A 𝐀 总计 B a b a+b 𝐁 c d c+d 总计 a+c b+d a+b+c+d 记 n=a+b+c+d,设 χ 2 = 𝒏(𝒂𝒅-𝒃𝒄) 𝟐 (𝒂+𝒃)(𝒄+𝒅)(𝒂+𝒄)(𝒃+𝒅)

任意给定一个α(称为显著性水平,通常取为0.05,0.01等),可以 找到满足条件Px≥)=a的数k(称为显著性水平a对应的分位 数).如果根据样本数据算出x的值后,发现≥k成立,就称在犯 错误的概率不超过α的前提下,可以认为A与B不独立(也称为 A与B有关);或说有1-的把握认为A与B有关若x2<k成立,就 称不能得到前述结论.这一过程通常称为独立性检验 (2)独立性检验通常得到的结果,或者是有1-α的把握认为A与 B有关,或者没有1-a的把握认为A与B有关
导航 任意给定一个α(称为显著性水平,通常取为0.05,0.01等),可以 找到满足条件P(χ 2≥k)=α的数k(称为显著性水平α对应的分位 数).如果根据样本数据算出χ 2的值后,发现χ 2≥k成立,就称在犯 错误的概率不超过α的前提下,可以认为A与B不独立(也称为 A与B有关);或说有1-α的把握认为A与B有关.若χ 2<k成立,就 称不能得到前述结论.这一过程通常称为独立性检验. (2)独立性检验通常得到的结果,或者是有1-α的把握认为A与 B有关,或者没有1-α的把握认为A与B有关
导则 3.做一做:对甲、乙两个班的学生在某次考试中的数学成绩 优秀和及格的人数进行统计,得到如下2×2列联表, 班级 数学成绩 优秀 及格 总计 甲班 11 34 45 乙班 8 37 45 总计 19 71 90 则随机变量x的值约为( A.0.600 B.0.828 C.2.712 D.6.004 答案:A
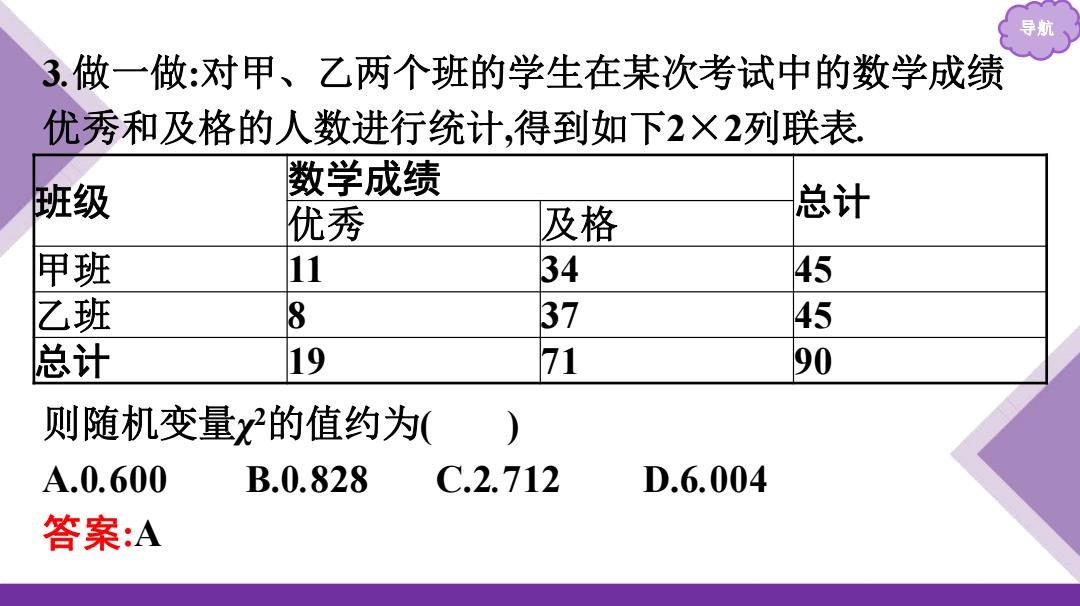
导航 3.做一做:对甲、乙两个班的学生在某次考试中的数学成绩 优秀和及格的人数进行统计,得到如下2×2列联表. 班级 数学成绩 总计 优秀 及格 甲班 11 34 45 乙班 8 37 45 总计 19 71 90 则随机变量χ 2的值约为( ) A.0.600 B.0.828 C.2.712 D.6.004 答案:A

导航 解析:根据2×2列联表中的数据,可得 X-90x1x37382≈0.60,故选A. 45×45×19×71
导航 解析:根据 2×2 列联表中的数据,可得 χ 2 = 𝟗𝟎×(𝟏𝟏×𝟑𝟕-𝟑𝟒×𝟖) 𝟐 𝟒𝟓×𝟒𝟓×𝟏𝟗×𝟕𝟏 ≈0.600.故选 A

导 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” (1)2×2列联表中的数据是两个事件的频数.( (2)事件A与B无关,即两个事件互不影响.( 3)x的大小是判断事件A与B是否相关的统计量.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)2×2列联表中的数据是两个事件的频数.( √ ) (2)事件A与B无关,即两个事件互不影响.( √ ) (3)χ 2的大小是判断事件A与B是否相关的统计量.( √ )