
全程设计 第四章 概率与统计 4.4 数学探究活动:了解高考选考科目 的确定是否与性别有关
第四章 概率与统计 4.4 数学探究活动:了解高考选考科目 的确定是否与性别有关

课标定位素养阐释 课堂·重难突破 随堂训练
课标定位 素养阐释 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.掌握用独立性检验解决实际问题的步骤 2.加强数学建模和数学运算能力的培养
导航 课标定位 素养阐释 1.掌握用独立性检验解决实际问题的步骤. 2.加强数学建模和数学运算能力的培养

导航 课堂·重难突破 探究独立性检验的实际应用 【例题】在一次天气恶劣的飞行航程中,调查了男女乘客在 飞机上晕机的情况:男乘客晕机的有24人,不晕机的有31人;女 乘客晕机的有8人,不晕机的有26人.根据所给数据,能否在犯 错误的概率不超过10%的前提下认为在天气恶劣的飞行航程 中,男乘客比女乘客更容易晕机?
导航 课堂·重难突破 探究 独立性检验的实际应用 【例题】在一次天气恶劣的飞行航程中,调查了男女乘客在 飞机上晕机的情况:男乘客晕机的有24人,不晕机的有31人;女 乘客晕机的有8人,不晕机的有26人.根据所给数据,能否在犯 错误的概率不超过10%的前提下认为在天气恶劣的飞行航程 中,男乘客比女乘客更容易晕机?
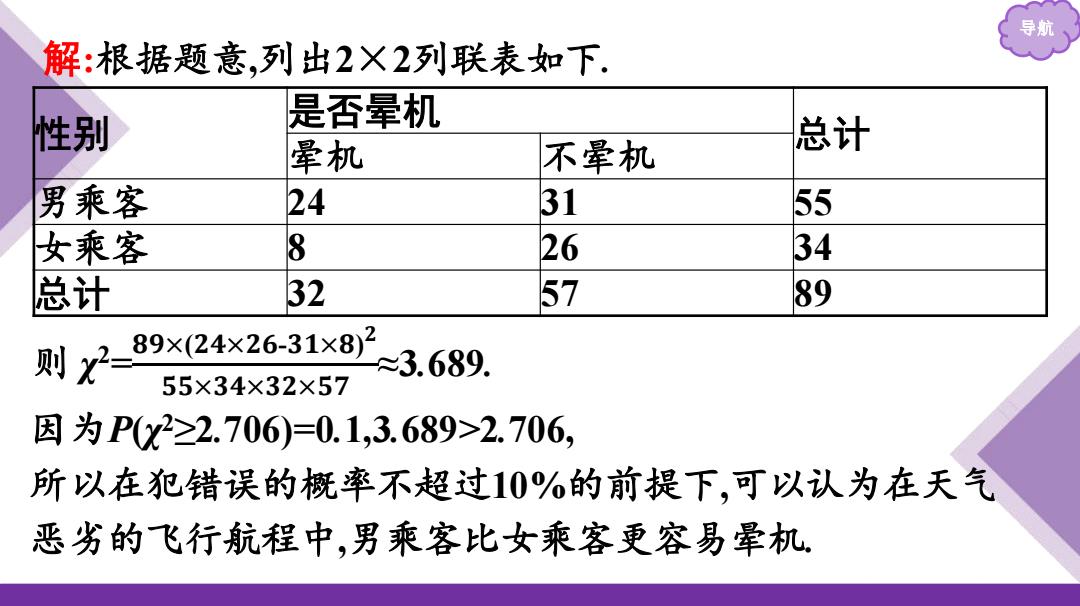
导航 解:根据题意,列出2×2列联表如下. 性别 是否晕机 晕机 不晕机 总计 男乘客 24 31 55 女乘客 8 26 34 总计 32 57 89 则x2 89×24×26-31×82 3.689. 55×34×32×57 因为Px2≥2.706)=0.1,3.689>2.706, 所以在犯错误的概率不超过10%的前提下,可以认为在天气 恶劣的飞行航程中,男乘客比女乘客更容易晕机
导航 解:根据题意,列出2×2列联表如下. 性别 是否晕机 总计 晕机 不晕机 男乘客 24 31 55 女乘客 8 26 34 总计 32 57 89 则 χ 2 = 𝟖𝟗×(𝟐𝟒×𝟐𝟔-𝟑𝟏×𝟖) 𝟐 𝟓𝟓×𝟑𝟒×𝟑𝟐×𝟓𝟕 ≈3.689. 因为P(χ 2≥2.706)=0.1,3.689>2.706, 所以在犯错误的概率不超过10%的前提下,可以认为在天气 恶劣的飞行航程中,男乘客比女乘客更容易晕机

导航 反思感悟 利用独立性检验解决实际问题的步骤: (1)根据相关数据,列出2×2列联表; (2)根据2×2列联表中的数据,计算x2的值; (3)比较x2与分位数; (4)得出结论
导航 利用独立性检验解决实际问题的步骤: (1)根据相关数据,列出2×2列联表; (2)根据2×2列联表中的数据,计算χ 2的值; (3)比较χ 2与分位数k; (4)得出结论

导 【变式训练】某大型企业人力资源部为了研究企业员工工 作积极性和对待企业改革态度的关系,随机抽取了189名员工 进行调查,所得数据如下表所示 工作情况 是否积极支持企业改革 积极支持企业改革不太赞成企业改革 总计 工作积极 54 40 94 工作一般 32 63 95 总计 86 103 189
导航 【变式训练】某大型企业人力资源部为了研究企业员工工 作积极性和对待企业改革态度的关系,随机抽取了189名员工 进行调查,所得数据如下表所示. 工作情况 是否积极支持企业改革 总计 积极支持企业改革 不太赞成企业改革 工作积极 54 40 94 工作一般 32 63 95 总计 86 103 189

对于人力资源部的研究项目,根据上述数据能得出什么结论? 李明和张宇都对该题进行了独立性检验的分析,李明的结论 是“在犯错误的概率不超过1%的前提下,认为企业员工的工 作积极性和对待企业改革的态度有关系”;张宇的结论是“在 犯错误的概率不超过0.5%的前提下,认为企业员工的工作积 极性和对待企业改革的态度有关系”. 他们两个的结论正确吗?为什么他们的结论不一样?
导航 对于人力资源部的研究项目,根据上述数据能得出什么结论? 李明和张宇都对该题进行了独立性检验的分析,李明的结论 是“在犯错误的概率不超过1%的前提下,认为企业员工的工 作积极性和对待企业改革的态度有关系”;张宇的结论是“在 犯错误的概率不超过0.5%的前提下,认为企业员工的工作积 极性和对待企业改革的态度有关系” . 他们两个的结论正确吗?为什么他们的结论不一样?

导航 解:由题意,可知 189x154×63-40x3210.759. 94×95×86×103 因为Px2≥6.635)=0.01,Px2≥7.879)=0.005,10.759>7.879>6.635, 所以李明和张宇的结论都正确 造成结论不一样的原因是他们两人采用了两种不同的判断规 则,即所选用的分位数k不同」
导航 解:由题意,可知 因为P(χ 2≥6.635)=0.01,P(χ 2≥7.879)=0.005,10.759>7.879>6.635, 所以李明和张宇的结论都正确. 造成结论不一样的原因是他们两人采用了两种不同的判断规 则,即所选用的分位数k不同. χ 2 = 𝟏𝟖𝟗×(𝟓𝟒×𝟔𝟑-𝟒𝟎×𝟑𝟐) 𝟐 𝟗𝟒×𝟗𝟓×𝟖𝟔×𝟏𝟎𝟑 ≈10.759

导航 随堂训练 1用旧设备和改造后的新设备冶炼某种金属,为了检验用这两 种设备生产的产品中所含杂质的关系,调查结果如下表所示 设备 含杂质的高低 杂质高 杂质低 旧设备 37 121 新设备 22 202
导航 随堂训练 1.用旧设备和改造后的新设备冶炼某种金属,为了检验用这两 种设备生产的产品中所含杂质的关系,调查结果如下表所示. 设备 含杂质的高低 杂质高 杂质低 旧设备 37 121 新设备 22 202