
全程设计 第四章 概率与统计 4.2 随机变量 4.2.2 离牧型随机变量的分布列
第四章 概率与统计 4.2 随机变量 4.2.2 离散型随机变量的分布列
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位 素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.通过具体实例,理解离散型随机变量的分布列 2.通过具体实例,了解伯努利试验 3.体会数学抽象的过程,加强数学建模和数据分析能力的培养
导航 课标定位 素养阐释 1.通过具体实例,理解离散型随机变量的分布列. 2.通过具体实例,了解伯努利试验. 3.体会数学抽象的过程,加强数学建模和数据分析能力的培养

导航 课前·基础认知 离散型随机变量的分布列 【问题思考】 1投掷一枚均匀的骰子,所得点数为X (1)X可取哪些数字? 提示:X=1,2,3,4,5,6. (2)当X取不同的值时,其概率P分别是多少? 提示:都等于
导航 课前·基础认知 一、离散型随机变量的分布列 【问题思考】 1.投掷一枚均匀的骰子,所得点数为X. (1)X可取哪些数字? 提示:X=1,2,3,4,5,6. (2)当X取不同的值时,其概率P分别是多少? 提示:都等于𝟏 𝟔
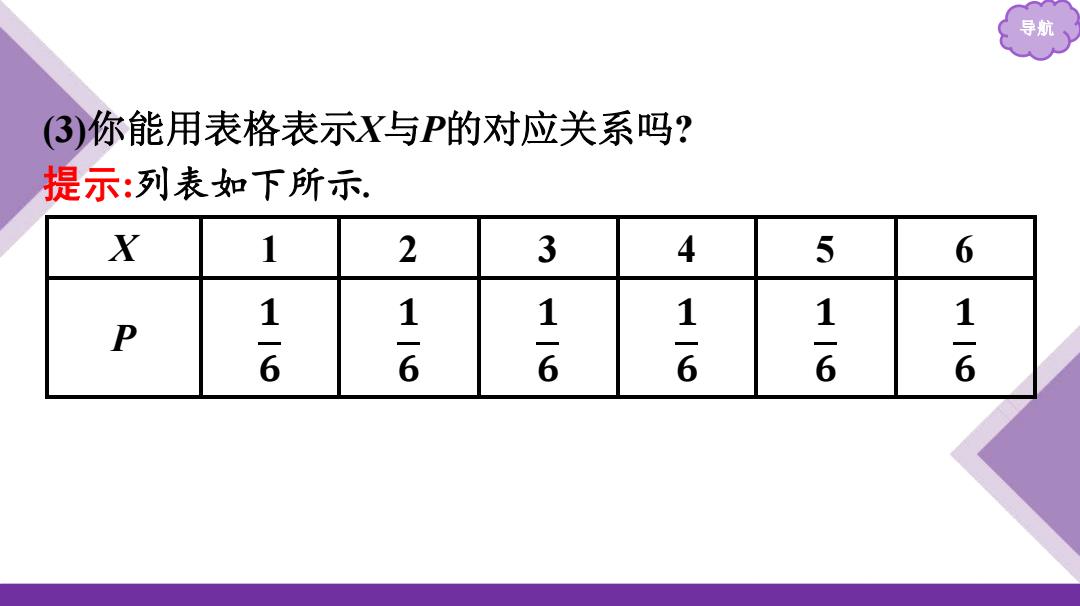
导航 (3)你能用表格表示X与P的对应关系吗? 提示:列表如下所示 X 1 2 3 4 5 6 P 1-6 1-6 1-6 1-6 1-6 1-6
导航 (3)你能用表格表示X与P的对应关系吗? 提示:列表如下所示. X 1 2 3 4 5 6 P 𝟏 𝟔 𝟏 𝟔 𝟏 𝟔 𝟏 𝟔 𝟏 𝟔 𝟏 𝟔
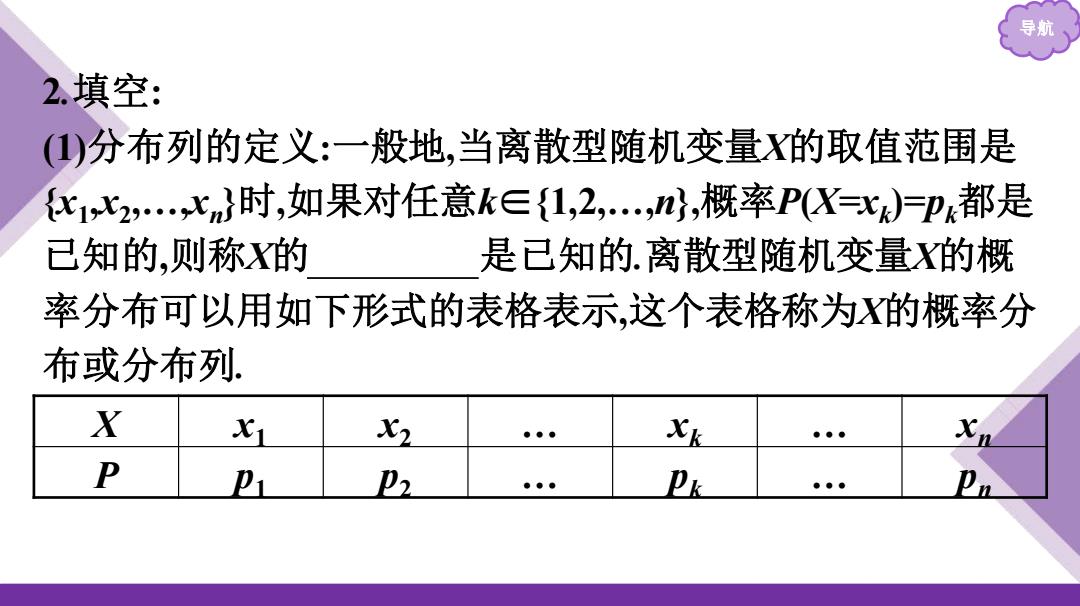
导航 2.填空: ()分布列的定义:一般地,当离散型随机变量X的取值范围是 {化1水2,…X}时,如果对任意k∈{1,2,,},概率P(X=式=p都是 已知的,则称X的 是已知的.离散型随机变量X的概 率分布可以用如下形式的表格表示,这个表格称为的概率分 布或分布列. X x1 X2 Xk P Pr 卫 Pk
导航 2.填空: (1)分布列的定义:一般地,当离散型随机变量X的取值范围是 {x1 ,x2 ,…,xn }时,如果对任意k∈{1,2,…,n},概率P(X=xk )=pk都是 已知的,则称X的 概率分布 是已知的.离散型随机变量X的概 率分布可以用如下形式的表格表示,这个表格称为X的概率分 布或分布列. X x1 x2 … xk … xn P p1 p2 … pk … pn

导航 2)分布列的性质: ①p2,k=1,2,3,,; n ② ∑pkp1tp2+.…tpm=_ k=
导航 (2)分布列的性质 : ①p k≥ 0 ,k=1,2,3,…, n ; ② ∑𝒌=𝟏𝒏 p k=p1+p 2 + …+p n = 1

导期 3做一做:设随机变量5的分布列为P(G==a((),=1,23,则a 的值为( 11 A.1 B. 13 3 13 答案:C 解析:由分布列的性质,得(侣+写+》1,得a韶
导航 3.做一做:设随机变量 ξ 的分布列为 P(ξ=i)= 𝐚 𝟏𝟑 𝐢,i=1,2,3, 则 a 的值为( ) A.1 B. 𝟗𝟏𝟑 C. 𝟐 𝟕 𝟏 𝟑 D. 𝟏 𝟏 𝟏 𝟑 答案 :C 解析:由分布列的性质,得 a 𝟏𝟑 + 𝟏𝟗 + 𝟏𝟐𝟕 =1, 得 a= 𝟐 𝟕 𝟏 𝟑

导航 二、两点分布 【问题思考】 1.利用随机变量研究一类问题,如抽取的奖券是否中奖,买回 的一件产品是否为正品,新生婴儿的性别,投篮是否命中等,这 些有什么共同点? 提示:这些问题的共同点是随机试验只有两个可能的结果
导航 二、两点分布 【问题思考】 1.利用随机变量研究一类问题,如抽取的奖券是否中奖,买回 的一件产品是否为正品,新生婴儿的性别,投篮是否命中等,这 些有什么共同点? 提示:这些问题的共同点是随机试验只有两个可能的结果
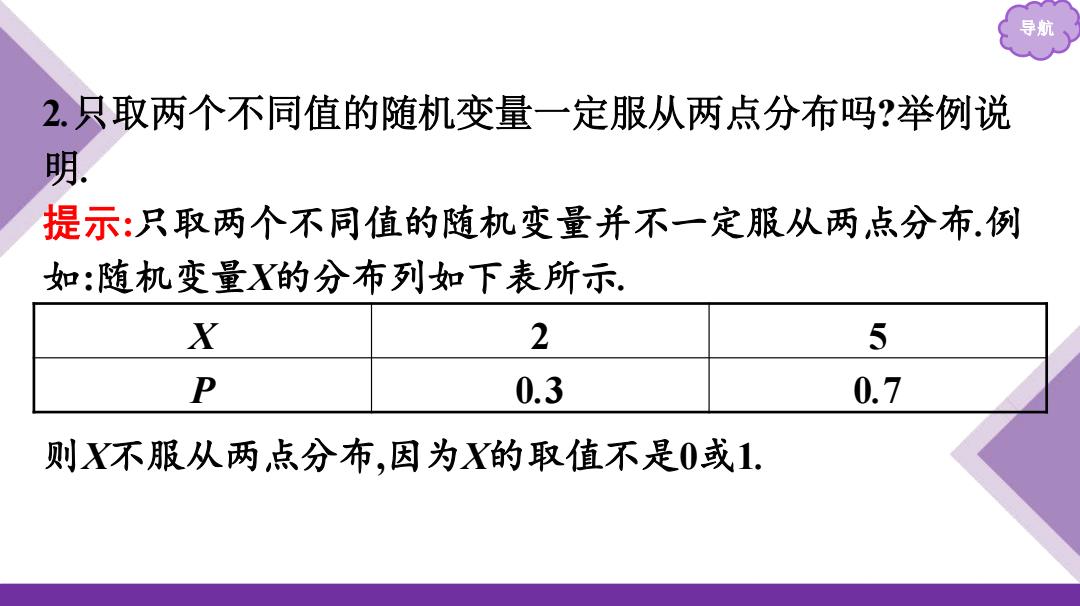
导航 2只取两个不同值的随机变量一定服从两点分布吗?举例说 明。 提示:只取两个不同值的随机变量并不一定服从两点分布.例 如:随机变量X的分布列如下表所示. X 2 5 D 0.3 0.7 则X不服从两,点分布,因为X的取值不是0或1
导航 2.只取两个不同值的随机变量一定服从两点分布吗?举例说 明. 提示:只取两个不同值的随机变量并不一定服从两点分布.例 如:随机变量X的分布列如下表所示. 则X不服从两点分布,因为X的取值不是0或1. X 2 5 P 0.3 0.7