
全程设计 第四章 概率与统计 4.2 随机变量 4.2.4 随机变量的数字特征 第2课时 离牧型随机变量的方差
第四章 概率与统计 4.2 随机变量 4.2.4 随机变量的数字特征 第2课时 离散型随机变量的方差
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位 素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.通过具体实例,理解离散型随机变量的方差 2.理解两点分布、二项分布的方差及方差的性质,并能解决简 单的实际问题 3.体会随机变量方差的数学抽象的过程,加强数据分析和数学 运算能力的培养」
导航 课标定位 素养阐释 1.通过具体实例,理解离散型随机变量的方差. 2.理解两点分布、二项分布的方差及方差的性质,并能解决简 单的实际问题. 3.体会随机变量方差的数学抽象的过程,加强数据分析和数学 运算能力的培养
导航 课前·基础认知 离散型随机变量的方差 【问题思考】 1.A,B两台机床同时加工零件,每加工一批数量较大的零件,出 现的次品数与对应的概率如下表 A机床: B机床: 次品 0 3 次品 数X1 0 2 数X P 0.7 0.2 0.060.04 0.8 0.060.040.1
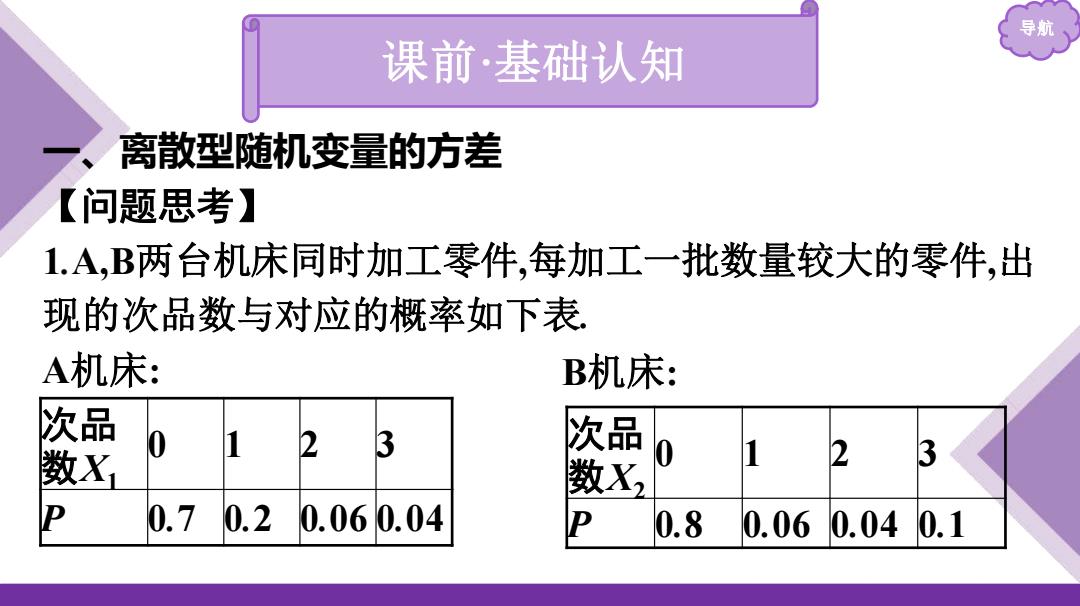
导航 课前·基础认知 一、离散型随机变量的方差 【问题思考】 1.A,B两台机床同时加工零件,每加工一批数量较大的零件,出 现的次品数与对应的概率如下表. A机床: 次品 数X1 0 1 2 3 P 0.7 0.2 0.06 0.04 B机床: 次品 数X2 0 1 2 3 P 0.8 0.06 0.04 0.1

导航 (1)EX)与EX2)有什么关系? 提示:EX1)=0×0.7+1×0.2+2×0.06+3×0.04=0.44, EX2)=0×0.8+1X0.06+2×0.04+3×0.1=0.44,EX)=EX2) (2)能说明两台机床加工零件的质量一样吗? 提示:不能. (3)还需利用什么指标才可以比较两台机床的加工质量? 提示:方差或标准差
导航 (1)E(X1 )与E(X2 )有什么关系? 提示:E(X1 )=0×0.7+1×0.2+2×0.06+3×0.04=0.44, E(X2 )=0×0.8+1×0.06+2×0.04+3×0.1=0.44,E(X1 )=E(X2 ). (2)能说明两台机床加工零件的质量一样吗? 提示:不能. (3)还需利用什么指标才可以比较两台机床的加工质量? 提示:方差或标准差

导期 2.填空:方差及标准差的定义 ()设离散型随机变量X的分布列如下表所示 X xI X2 Xk Xn P 卫2 卫k Pn 因为X的均值为E),所以D)= 能够刻画X 相对于均值的离散程度(或波动大小),这称为离散型随机变量 X的方差离散型随机变量X的方差D)也可用DX表示 (2)一般地√D☒称为离散型随机变量X的标准差,它也可以 刻画一个离散型随机变量的离散程度(或波动大小)
导航 2.填空:方差及标准差的定义 (1)设离散型随机变量X的分布列如下表所示. X x1 x2 … xk … xn P p1 p2 … pk … pn 因为X的均值为E(X),所以D(X)= ∑ 𝒊=𝟏 𝒏 [xi-E(X)]2 pi 能够刻画X 相对于均值的离散程度(或波动大小),这称为离散型随机变量 X 的方差.离散型随机变量 X 的方差 D(X)也可用 DX 表示. (2)一般地, 𝐃(𝐗)称为离散型随机变量 X 的标准差,它也可以 刻画一个离散型随机变量的离散程度(或波动大小)

导航 3.做一做:已知离散型随机变量X的可能取值为x1二1,x20, x3=1,且EX)=0.1,DX)=0.89,则x1水23对应的概率p1P23分别 为 答案:0.4 0.10.5
导航 3.做一做:已知离散型随机变量X的可能取值为x1 =-1,x2 =0, x3 =1,且E(X)=0.1,D(X)=0.89,则x1 ,x2 ,x3对应的概率p1 ,p2 ,p3分别 为 , , . 答案:0.4 0.1 0.5

导航 解析:由题意可知, P1+p2+p3=1, -p1+p3=0.1, 1.21p1+0.01p2+0.81p3=0.89, P1=0.4, 解得{卫2=0.1, p3=0.5
导航 解析 :由题意可知, 𝒑𝟏 + 𝒑𝟐 + 𝒑𝟑 = 𝟏, -𝒑𝟏 + 𝒑𝟑 = 𝟎.𝟏, 𝟏.𝟐𝟏𝒑𝟏 + 𝟎.𝟎𝟏𝒑𝟐 + 𝟎.𝟖𝟏𝒑𝟑 = 𝟎.𝟖𝟗, 解得 𝒑 𝟏 = 𝟎.𝟒, 𝒑𝟐 = 𝟎.𝟏, 𝒑𝟑 = 𝟎.𝟓

导航 二、几类特殊分布的方差与方差的性质 【问题思考】 1.已知随机变量X服从参数为p的两点分布,其分布列为 X 1 0 P 1-p (1)两点分布的方差D)与参数即有什么关系? 提示:D)=p(1-p) (2)若随机变量Y=2X+1,则D()与D)有什么关系? 提示:D(Y)=4DX)
导航 二、几类特殊分布的方差与方差的性质 【问题思考】 1.已知随机变量X服从参数为p的两点分布,其分布列为 X 1 0 P p 1-p (1)两点分布的方差D(X)与参数p有什么关系? 提示:D(X)=p(1-p). (2)若随机变量Y=2X+1,则D(Y)与D(X)有什么关系? 提示:D(Y)=4D(X)

导航 2填空:(1)若X服从参数为p的两点分布,则D)= (2)若X服从参数为n,p的二项分布,即X~B(np), 则D(X)= (3)方差的性质:若X与Y都是离散型随机变量,且Y=X+b(0), 则D(Y)=
导航 2.填空:(1)若X服从参数为p的两点分布,则D(X)= p(1-p) . (2)若X服从参数为n,p的二项分布,即X~B(n,p), 则D(X)= np(1-p) . (3)方差的性质:若X与Y都是离散型随机变量,且Y=aX+b(a≠0), 则D(Y)= a 2D(X)