
全程设计 复习课 第1课时 排列、组合与二项式定理
复习课 第1课时 排列、组合与二项式定理

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破
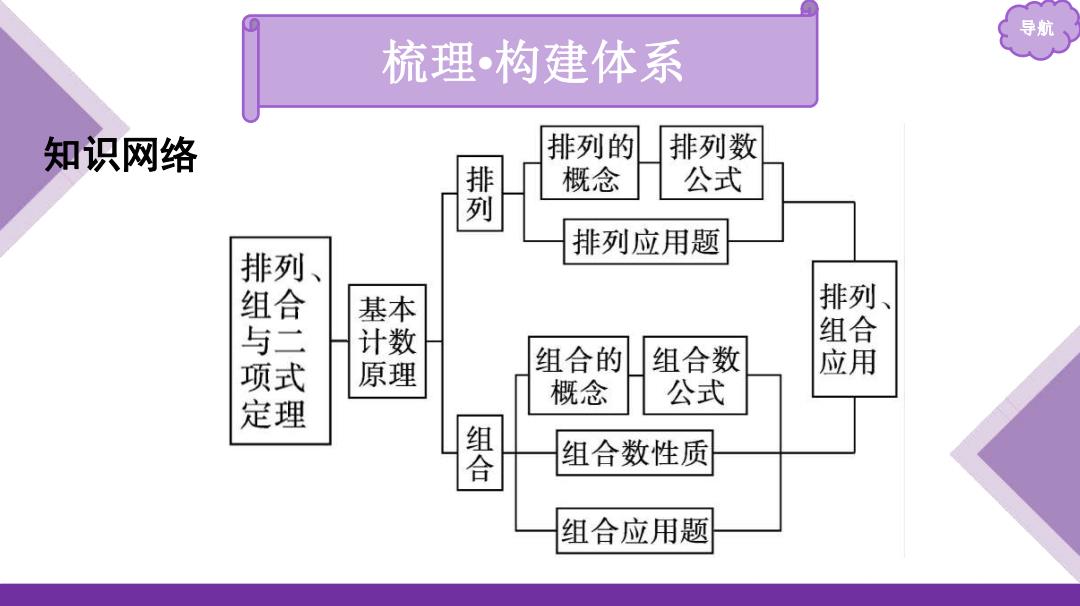
导航 梳理•构建体系 知识网络 排列的 排列数 概念 公式 列 排列应用题 排列 组合 基本 排列、 计数 组合 项式 原理 组合的 组合数 应用 概念 公式 定理 合 组合数性质 组合应用题
导航 梳理 •构建体系 知识网 络
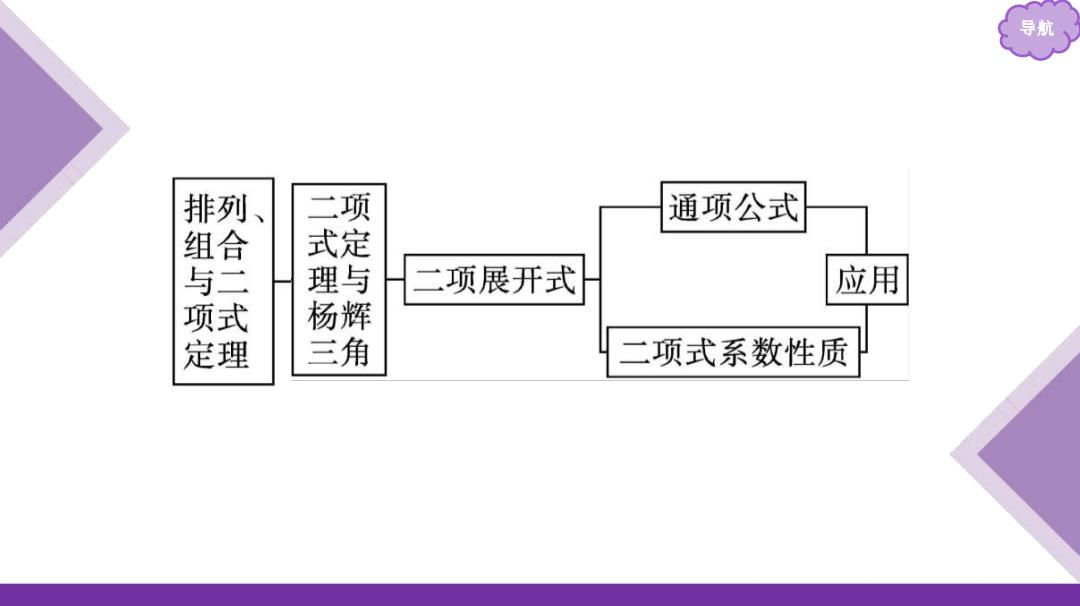
导航 排列 二项 通项公式 二项展开式 应用 杨辉 定理 二项式系数性质
导航

要点梳理 1.两个基本计数原理的内容是什么? 提示:(1)分类加法计数原理:完成一件事,如果有类办法,且: 第一类办法中有m,种不同的方法,第二类办法中有m,种不同 的方法...第n类办法中有m,种不同的方法,那么完成这件事 共有N=m1+m2+..+mn种不同的方法. (2)分步乘法计数原理:完成一件事,如果需要分成个步骤,且: 做第一步有m,种不同的方法,做第二步有m种不同的方 法..做第n步有mn种不同的方法,那么完成这件事共有 N=m1X2X.…Xmn种不同的方法
导航 要点梳理 1.两个基本计数原理的内容是什么? 提示:(1)分类加法计数原理:完成一件事,如果有n类办法,且: 第一类办法中有m1种不同的方法,第二类办法中有m2种不同 的方法……第n类办法中有mn种不同的方法,那么完成这件事 共有N=m1+m2+…+mn种不同的方法. (2)分步乘法计数原理:完成一件事,如果需要分成n个步骤,且: 做第一步有m1种不同的方法,做第二步有m2种不同的方 法……做第n步有mn种不同的方法,那么完成这件事共有 N=m1×m2×…×mn种不同的方法

2.排列数与组合数公式是什么?各有什么性质?请完成下表 内容 排列与排列数 组合与组合数 排列数公式Am=n(n-1) 组合数公式CT= 公式 A册 n! n(n-1)..[n-(m-1)月 n! (n-m)! m×(m-1)×..×2×1 (n-m)!m! 性质 当m=n时,Am为全排 C9=Ch=1; = 列;A=n!;0!= CH C+C-1 备注 n,m∈N+,且sn
导航 2.排列数与组合数公式是什么?各有什么性质?请完成下表. 内容 排列与排列数 组合与组合数 公式 排列数公式𝑨𝐧 𝐦=n(n-1) … [n-(m-1)] = 𝐧! (𝐧-𝐦)! 组合数公式𝑪𝐧 𝐦 = 𝑨𝐧 𝐦 𝑨 𝐦 𝐦 = 𝐧(𝐧-𝟏)…[𝐧-(𝐦-𝟏)] 𝐦×(𝐦-𝟏)×…×𝟐×𝟏 = 𝐧! (𝐧-𝐦)!𝐦! 性质 当 m=n 时,𝑨𝐧 𝐦 为全排 列;𝑨𝐧 𝐧 =n!;0!= 1 𝑪𝐧 𝟎 = 𝑪𝐧 𝐧 =1; 𝑪𝐧 𝐦 = 𝑪𝐧 𝐧-𝐦 ; 𝑪𝐧 𝐦 + 𝑪𝐧 𝐦-𝟏 = 𝑪𝐧+𝟏 𝐦 备注 n,m∈N+,且 m≤n

导航 3.二项式定理的内容是什么?二项展开式的通项公式是什么? 提示:()二项式定理的内容: (a+b)"=CQa"+Cna"-b+...+Cka"kbk+...+Cnb"(nEN+). (2)通项公式:Tk+1=Ckd-b,k∈{0,1,2,…,n
导航 3.二项式定理的内容是什么?二项展开式的通项公式是什么? 提示:(1)二项式定理的内容: (a+b) n =𝐂𝒏 𝟎 a n +𝐂𝒏 𝟏 a n-1 b+…+𝐂𝒏 𝒌 a n-k b k +…+𝐂𝒏 𝒏 b n (n∈N+). (2)通项公式:Tk+1=𝐂𝒏 𝒌 a n-k b k ,k∈{0,1,2,…,n}

导 4二项式系数有哪些性质?二项式系数的和是什么? 提示:(1)与首末两端等距离的两个二项式系数相等, (2)当n是偶数时,中间一项(第?+1项)的二项式系数最大; 当n是奇数时,中间两项(第”项和第”牛+1项)的二项式系数 相等且最大. (3)C%+C7+C+..+Cn=2
导航 4.二项式系数有哪些性质?二项式系数的和是什么? 提示:(1)与首末两端等距离的两个二项式系数相等. (2)当 n 是偶数时,中间一项 第 𝒏 𝟐 + 𝟏项 的二项式系数最大; 当 n 是奇数时,中间两项(第 𝒏+𝟏 𝟐 项和第𝒏+𝟏 𝟐 +1 项)的二项式系数 相等且最大. (3)𝐂𝒏 𝟎 + 𝐂𝒏 𝟏 + 𝐂𝒏 𝟐 +…+𝐂𝒏 𝒏 =2 n

思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“义”. (1)在分类加法计数原理中,两类不同方案中的方法可以相同. (2)在分步乘法计数原理中,事情是分两步完成的,其中任何一 个单独的步骤都能完成这件事( (3)所有元素完全相同的两个排列为相同排列.( (4)一个组合中取出的元素讲究元素的先后顺序.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)在分类加法计数原理中,两类不同方案中的方法可以相同. ( × ) (2)在分步乘法计数原理中,事情是分两步完成的,其中任何一 个单独的步骤都能完成这件事.( × ) (3)所有元素完全相同的两个排列为相同排列.( × ) (4)一个组合中取出的元素讲究元素的先后顺序.( × )

导航 ⑤)若组合式C=C,则x=m成立.( (6)n+1)!-n.=nn.() (7)kck=nC:1.( (8)Cd-b是二项展开式的第k项.( (9)二项展开式中,系数最大的项为中间一项或中间两项! (10)(a+b)的展开式中某一项的二项式系数与,b无关.( (11)(+b)"的展开式中某项的系数是该项中非字母因数部分, 包括符号等,与该项的二项式系数不同(
导航 (5)若组合式𝐂𝒏 𝒙 = 𝐂𝒏 𝒎,则 x=m 成立.( × ) (6)(n+1)!-n!=n·n!.( √ ) (7)k𝐂𝒏 𝒌 =n𝐂𝒏-𝟏 𝒌-𝟏 .( √ ) (8)𝐂𝒏 𝒌 a n-k b k 是二项展开式的第 k 项.( × ) (9)二项展开式中,系数最大的项为中间一项或中间两项. ( × ) (10)(a+b) n的展开式中某一项的二项式系数与a,b无关.( √ ) (11)(a+b) n的展开式中某项的系数是该项中非字母因数部分, 包括符号等,与该项的二项式系数不同.( √ )