
全程设计 第四章 概率与统计 4.2 随机变量 4.2.3 二须分布与超几何分布 第2课时 超几何分布
第四章 概率与统计 4.2 随机变量 4.2.3 二项分布与超几何分布 第2课时 超几何分布
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位 素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1通过具体实例,了解超几何分布,并能解决简单的实际问题 2.体会数学抽象的过程,加强数学建模和数学运算能力的培养
导航 课标定位 素养阐释 1.通过具体实例,了解超几何分布,并能解决简单的实际问题. 2.体会数学抽象的过程,加强数学建模和数学运算能力的培养

导航 课前·基础认知 超几何分布的概念 【问题思考】 1.从有5名男生的100名学生中任选3人 (1)其中恰有1名男生的概率是多少? 提示c堡 Cioo (2)其中恰有2名男生的概率是多少? 提示: os 300
导航 课前·基础认知 超几何分布的概念 【问题思考】 1.从有5名男生的100名学生中任选3人. (1)其中恰有1名男生的概率是多少? (2)其中恰有2名男生的概率是多少? 提示: 𝐂𝟓 𝟏 𝐂𝟗𝟓 𝟐 𝐂𝟏𝟎𝟎 𝟑 . 提示: 𝐂𝟓 𝟐 𝐂𝟗𝟓 𝟏 𝐂𝟏𝟎𝟎 𝟑

导 2.填空:一般地,若有总数为N件的甲、乙两类物品,其中甲类 有M件(M<N),从所有物品中随机取出n件(≤N,则这n件中所 含甲类物品数X是一个离散型随机变量X能取不小于且不大 于s的所有自然数,其中s是M与n中的较小者,t在n不大于乙类 物品件数(即nsN-0时取0,否则t取n减乙类物品件数之差(即 t=n-N-M0),而且PX=k= C疏CR ,k=t,t什1,…,S, CN 这里的X称为服从参数为N,n,M的超几何分布,记作
导航 2.填空:一般地,若有总数为N件的甲、乙两类物品,其中甲类 有M件(M<N),从所有物品中随机取出n件(n≤N),则这n件中所 含甲类物品数X是一个离散型随机变量,X能取不小于t且不大 于s的所有自然数,其中s是M与n中的较小者,t在n不大于乙类 物品件数(即n≤N-M)时取0,否则t取n减乙类物品件数之差(即 t=n-(N-M)),而且P(X=k)= ,k=t,t+1,…,s, 这里的X称为服从参数为N,n,M的超几何分布,记作 X~H(N,n,M) . 𝑪 𝑴 𝒌 𝑪𝑵−𝑴 𝒏−𝒌 𝑪𝑵 𝒏
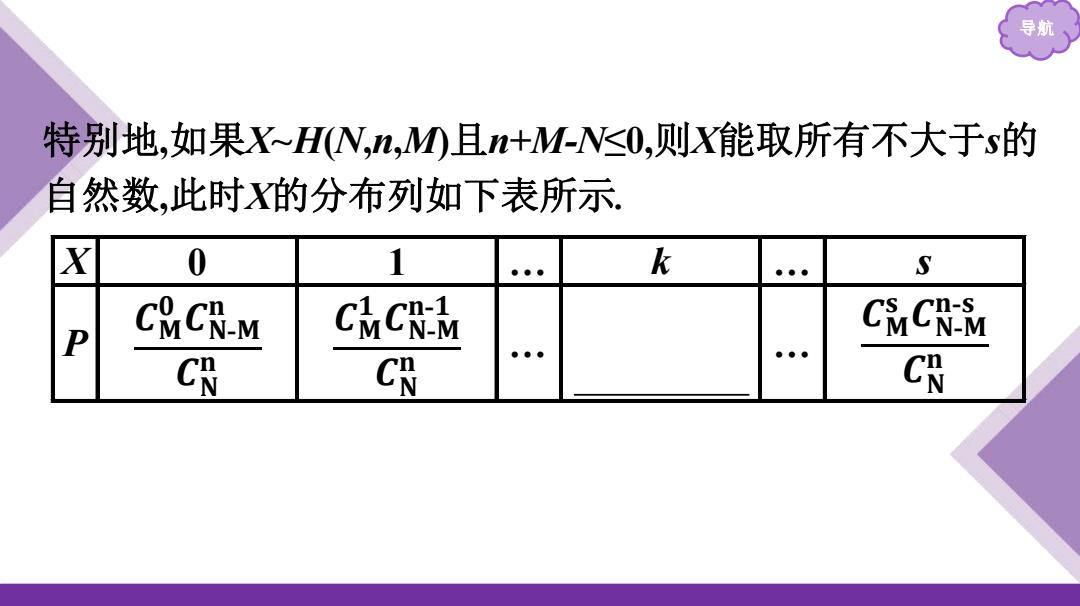
导航 特别地,如果X~HN,n,0且n+M-N≤0,则X能取所有不大于s的 自然数,此时X的分布列如下表所示 X 0 1 ●●● k S P CMCN-M CMCN-M CMCNM C囧 囧 ●… C囧
导航 特别地,如果X~H(N,n,M)且n+M-N≤0,则X能取所有不大于s的 自然数,此时X的分布列如下表所示. X 0 1 … k … s P 𝑪𝐌 𝟎 𝑪𝐍-𝐌 𝐧 𝑪𝐍 𝐧 𝑪𝐌 𝟏 𝑪𝐍-𝐌 𝐧-𝟏 𝑪𝐍 𝐧 … 𝑪𝐌 𝐤 𝑪𝐍-𝐌 𝐧-𝐤 𝑪𝐍 𝐧 … 𝑪𝐌 𝐬 𝑪𝐍-𝐌 𝐧-𝐬 𝑪𝐍 𝐧

导月 3.做一做:已知从4名男生和2名女生中任选3人参加数学竞赛, 则所选3人中,女生不超过1人的概率为 答案 解析:设所选女生的人数为X,则XH(6,3,2), 故PO≤I=PX=0+PK=I)-gs 4
导航 3.做一做:已知从4名男生和2名女生中任选3人参加数学竞赛, 则所选3人中,女生不超过1人的概率为 . 答案: 𝟒 𝟓 解析:设所选女生的人数为 X,则 X~H(6,3,2), 故 P(X≤1)=P(X=0)+P(X=1)= 𝐂𝟐 𝟎 𝐂𝟒 𝟑 𝐂𝟔 𝟑 + 𝐂𝟐 𝟏 𝐂𝟒 𝟐 𝐂𝟔 𝟑 = 𝟒 𝟓

导期 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√,错 误的画“X” (1)从4名男演员和3名女演员中选出4人,其中女演员的人数X 服从超几何分布.( (2)袋中有3个白球、4个黑球,每次从中取出1个球,有放回地 取3次,则白球的个数X服从超几何分布.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“×” . (1)从4名男演员和3名女演员中选出4人,其中女演员的人数X 服从超几何分布.( √ ) (2)袋中有3个白球、4个黑球,每次从中取出1个球,有放回地 取3次,则白球的个数X服从超几何分布.( × )

导航 课堂·重难突破 探究一超几何分布 【例1】一个袋中装有6个大小、质地完全相同的小球,其中 红球有3个,编号为1,2,3;黑球有2个,编号为1,2;白球有1个,编 号为1现从袋中一次随机取出3个球 (1)求取出的3个球的颜色都不相同的概率; (2)记取出编号为1的球的个数为X,求X的分布列
导航 课堂·重难突破 探究一 超几何分布 【例1】一个袋中装有6个大小、质地完全相同的小球,其中 红球有3个,编号为1,2,3;黑球有2个,编号为1,2;白球有1个,编 号为1.现从袋中一次随机取出3个球. (1)求取出的3个球的颜色都不相同的概率; (2)记取出编号为1的球的个数为X,求X的分布列

导航 解:(1)从袋中一次随机取出3个球,取法总数为C=20,取出的 3个球的颜色都不相同的取法种数为C3C2C1=6,故取出的3个 球的颜色都不相同的概率为P品0= 10 (2)由题意可知,X~H(6,3,3), 则P(X=0)= c- c昭 20 PX=1)= 9 c 203
导航 解:(1)从袋中一次随机取出 3 个球,取法总数为𝐂𝟔 𝟑 =20,取出的 3个球的颜色都不相同的取法种数为𝐂𝟑 𝟏 𝐂𝟐 𝟏 𝐂𝟏 𝟏 =6,故取出的3个 球的颜色都不相同的概率为 P= 𝟔 𝟐𝟎 = 𝟑 𝟏𝟎 . (2)由题意可知,X~H(6,3,3), 则 P(X=0)= 𝐂𝟑 𝟎 𝐂𝟑 𝟑 𝐂𝟔 𝟑 = 𝟏 𝟐𝟎 , P(X=1)= 𝐂𝟑 𝟏 𝐂𝟑 𝟐 𝐂𝟔 𝟑 = 𝟗 𝟐𝟎