
全程设计 4.3 ,统计模型 4.3.1 一元线性回归模型 第1时 相关关系、回归直线方程 回归直线方程的性质
4.3 统计模型 4.3.1 一元线性回归模型 第1课时 相关关系、回归直线方程、 回归直线方程的性质
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位 素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.理解两个变量的相关关系的概念,会利用散点图判断两个变 量是否具有相关关系 2.了解一元线性回归模型及最小二乘法,会求回归直线方程 3.针对实际问题,会用一元线性回归模型进行预测, 4.体会数学建模的过程,加强数学抽象和数学运算能力的培养
导航 课标定位 素养阐释 1.理解两个变量的相关关系的概念,会利用散点图判断两个变 量是否具有相关关系. 2.了解一元线性回归模型及最小二乘法,会求回归直线方程. 3.针对实际问题,会用一元线性回归模型进行预测. 4.体会数学建模的过程,加强数学抽象和数学运算能力的培养

导航 课前·基础认知 一、相关关系 【问题思考】 1.正方形的边长x与周长y之间有什么关系? 提示:y=4北,当x确定时y也确定, 2.在一定范围内,当施肥量确定时,粮食产量是一个确定的值 吗? 提示:不是
导航 课前·基础认知 一、相关关系 【问题思考】 1.正方形的边长x与周长y之间有什么关系? 提示:y=4x,当x确定时,y也确定. 2.在一定范围内,当施肥量确定时,粮食产量是一个确定的值 吗? 提示:不是

导期 3填空: ()相关关系:两个变量之间经常存在着相互影响、相互依赖 的关系这些关系常见的有两类,一类是变量之间的关系具有 确定性,当一个变量确定后,另一个变量就确定了;另一类是变 量之间确实有一定的关系,但没有达到可以互相决定的程度, 它们之间的关系带有一定的 ,这两个变量的关系,统计 学上称为相关关系
导航 3.填空: (1)相关关系:两个变量之间经常存在着相互影响、相互依赖 的关系.这些关系常见的有两类,一类是变量之间的关系具有 确定性,当一个变量确定后,另一个变量就确定了;另一类是变 量之间确实有一定的关系,但没有达到可以互相决定的程度, 它们之间的关系带有一定的 随机性 ,这两个变量的关系,统计 学上称为相关关系
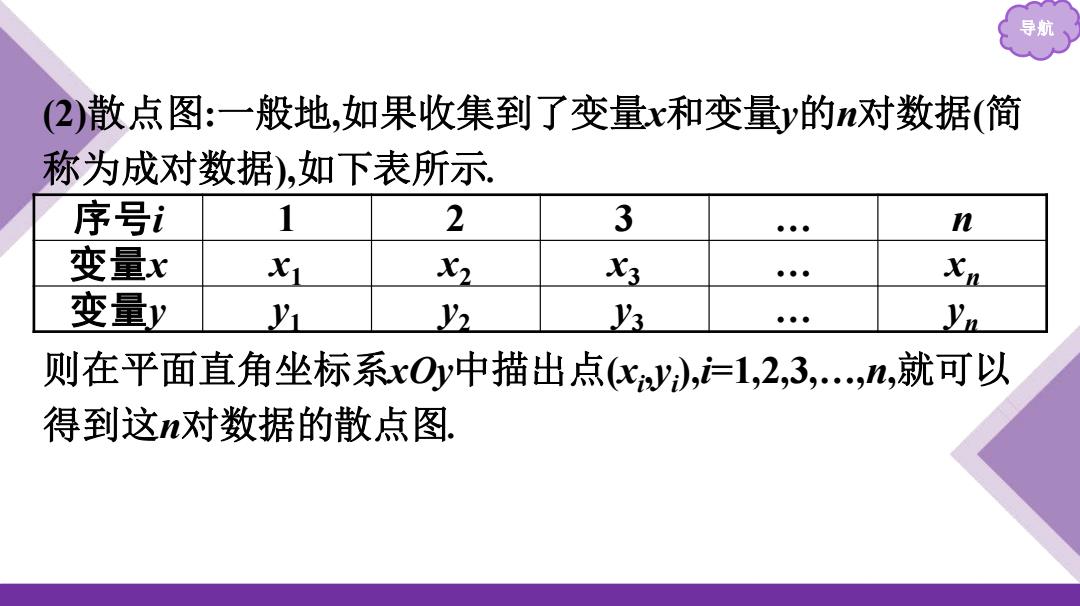
导 (2)散点图:一般地,如果收集到了变量x和变量y的n对数据(简 称为成对数据),如下表所示 序号i 1 2 3 ●●p n 变量x x1 X2 X3 ●●● Xn 变量y /i V2 V3 Yn 则在平面直角坐标系xOy中描出点(cy),i=1,2,3,,n,就可以 得到这n对数据的散点图
导航 (2)散点图:一般地,如果收集到了变量x和变量y的n对数据(简 称为成对数据),如下表所示. 序号i 1 2 3 … n 变量x x1 x2 x3 … xn 变量y y1 y2 y3 … yn 则在平面直角坐标系xOy中描出点(xi ,yi ),i=1,2,3,…,n,就可以 得到这n对数据的散点图

导 3)线性相关:如果由变量的成对数据、散点图或直观经验可 知,变量x与变量y之间的关系可以近似地用 来刻画, 则称x与y线性相关此时,如果一个变量增大,另一个变量大体 上也增大,则称这两个变量 ;如果一个变量增大,另一 个变量大体上,则称这两个变量负相关
导航 (3)线性相关:如果由变量的成对数据、散点图或直观经验可 知,变量x与变量y之间的关系可以近似地用 一次函数 来刻画, 则称x与y线性相关.此时,如果一个变量增大,另一个变量大体 上也增大,则称这两个变量正相关 ;如果一个变量增大,另一 个变量大体上 减少 ,则称这两个变量负相关

导航 4.做一做:下列说法正确的是( A.任何两个变量之间都有相关关系 B.根据身高和体重的相关关系可以确定身高对应的体重值 C相关关系是一种不确定的关系 D.以上说法都不正确 答案:C
导航 4.做一做:下列说法正确的是( ) A.任何两个变量之间都有相关关系 B.根据身高和体重的相关关系可以确定身高对应的体重值 C.相关关系是一种不确定的关系 D.以上说法都不正确 答案:C

导 二、回归直线方程 【问题思考】 1.如果变量x与线性相关,那么x与y的关系可以近似地用哪个 函数来刻画? 提示:一次函数 2.一次函数的解析式是什么?要求一次函数的解析式,需要求 出哪些参数? 提示:y=c+b(k0),需要求出k和b的值
导航 二、回归直线方程 【问题思考】 1.如果变量x与y线性相关,那么x与y的关系可以近似地用哪个 函数来刻画? 提示:一次函数. 2.一次函数的解析式是什么?要求一次函数的解析式,需要求 出哪些参数? 提示:y=kx+b(k≠0),需要求出k和b的值

3填空: ()回归直线方程:一般地,已知变量x与y的n对成对数据 (y),i=1,2,3,.,n.任意给定一个一次函数y=bx+,对每一个 已知的x,由直线方程可以得到一个估计值y=bx十,如果一 次函数y=bx+a能使(y1y)2+(y2y2)2+..+(ynym)2 n =∑yry)2取得最小值,则y=bx+a称为y关于x的回归直 i=1 线方程(对应的直线称为回归直线)
导航 3 .填空: (1)回归直线方程:一般地,已知变量 x 与 y 的 n 对成对数据 (xi,yi),i=1,2,3,…,n.任意给定一个一次函数 y=bx+a,对每一个 已知的 xi,由直线方程可以得到一个估计值 𝒚^𝐢 =bxi+a,如果一 次函数 𝐲^ = 𝒃^ x+ 𝒂^ 能使(𝒚^ 𝟏-y1)2 +(𝒚^ 𝟐-y 2)2 + … +(𝒚^ 𝒏-y n)2 = ∑𝒊=𝟏𝒏 (yi-𝒚^𝒊)2 取得最小值,则 𝒚^ = 𝒃^ x+ 𝒂^ 称为 y 关于 x 的回归直 线方程(对应的直线称为回归直线)