
全程设计 第四章 概率与统计 4.3 统计模型 4.3.1 一元线性回归模型 第2课时 相关系数、非线性回归
第四章 概率与统计 4.3 统计模型 4.3.1 一元线性回归模型 第2课时 相关系数、非线性回归
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位 素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.结合实例,了解相关系数的统计含义 2.会利用相关系数判断两个变量的相关性. 3.会根据数据求非线性回归方程, 4.体会数学建模的过程,加强数据分析和数学运算能力的培养
导航 课标定位 素养阐释 1.结合实例,了解相关系数的统计含义. 2.会利用相关系数判断两个变量的相关性. 3.会根据数据求非线性回归方程. 4.体会数学建模的过程,加强数据分析和数学运算能力的培养

导航 课前·基础认知 相关系数 【问题思考】 1.具有相关关系的两个变量的回归直线方程为y=bx+a. Λ (1)预报值y与真实值y一定一样吗? 提示:不一定
导航 课前·基础认知 一、相关系数 【问题思考】 1.具有相关关系的两个变量的回归直线方程为𝒚 ^ = 𝐛 ^ x+𝒂 ^ . (1)预报值𝒚 ^ 与真实值 y 一定一样吗? 提示:不一定

导航 (2)预报值y与真实值y之间的误差是越大越好还是越小越好? 提示:越小越好
导航 (2)预报值 与真实值y之间的误差是越大越好还是越小越好? 提示:越小越好. y ^
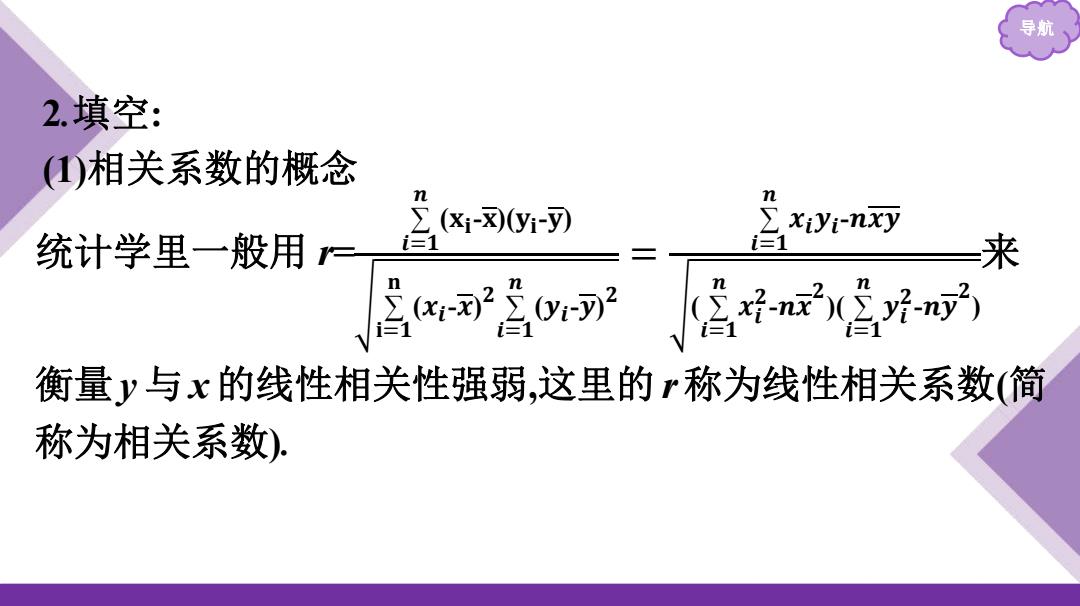
导航 2.填空: 相关系数的概念 n n (&1-8)y1-可) xiyi-nxy 统计学里一般用= 来 n :含02 衡量y与x的线性相关性强弱,这里的r称为线性相关系数(简 称为相关系数)
导航 2 .填空 : (1)相关系数的概念 统计学里一般用 r= ∑𝒊=𝟏𝒏 (𝐱𝐢-𝐱)( 𝐲𝐢-𝐲) ∑𝐢=𝟏𝐧 (𝒙𝒊-𝒙)𝟐 ∑𝒊=𝟏𝒏 (𝒚𝒊-𝒚)𝟐 = ∑𝒊=𝟏𝒏 𝒙𝒊𝒚𝒊-𝒏 𝒙 𝒚 ( ∑𝒊=𝟏𝒏 𝒙𝒊𝟐-𝒏 𝒙 𝟐 )( ∑𝒊=𝟏𝒏 𝒚𝒊𝟐-𝒏 𝒚 𝟐)来 衡量 y 与 x 的线性相关性强弱,这里的 r称为线性相关系数(简 称为相关系数)

导 2)相关系数的性质 ①≤1,且y与x正相关的充要条件是y与x负相关的充要 条件是 ②越小,说明两个变量之间的线性相关性 ,也就是得出 的回归直线方程越没有价值,即方程越不能反映真实的情 况r ,说明两个变量之间的线性相关性越强,也就是得 出的回归直线方程越有价值; 的充要条件是成对数据构成的点都在回归直线上
导航 (2)相关系数的性质 ①|r|≤1,且y与x正相关的充要条件是 r>0 ,y与x负相关的充要 条件是 r<0 ; ②|r|越小,说明两个变量之间的线性相关性 越弱 ,也就是得出 的回归直线方程越没有价值,即方程越不能反映真实的情 况;|r| 越大 ,说明两个变量之间的线性相关性越强,也就是得 出的回归直线方程越有价值; ③ |r|=1 的充要条件是成对数据构成的点都在回归直线上

导期 3.做一做:若分别计算具有线性相关关系的甲组数据和乙组 数据,得相关系数r甲=0.8,z二0.9,则相关关系较强的是( A.甲组数据 B.乙组数据 C.甲、乙两组数据一样强 D.不确定 答案:B
导航 3.做一做:若分别计算具有线性相关关系的甲组数据和乙组 数据,得相关系数r甲=0.8,r乙=-0.9,则相关关系较强的是( ) A.甲组数据 B.乙组数据 C.甲、乙两组数据一样强 D.不确定 答案:B
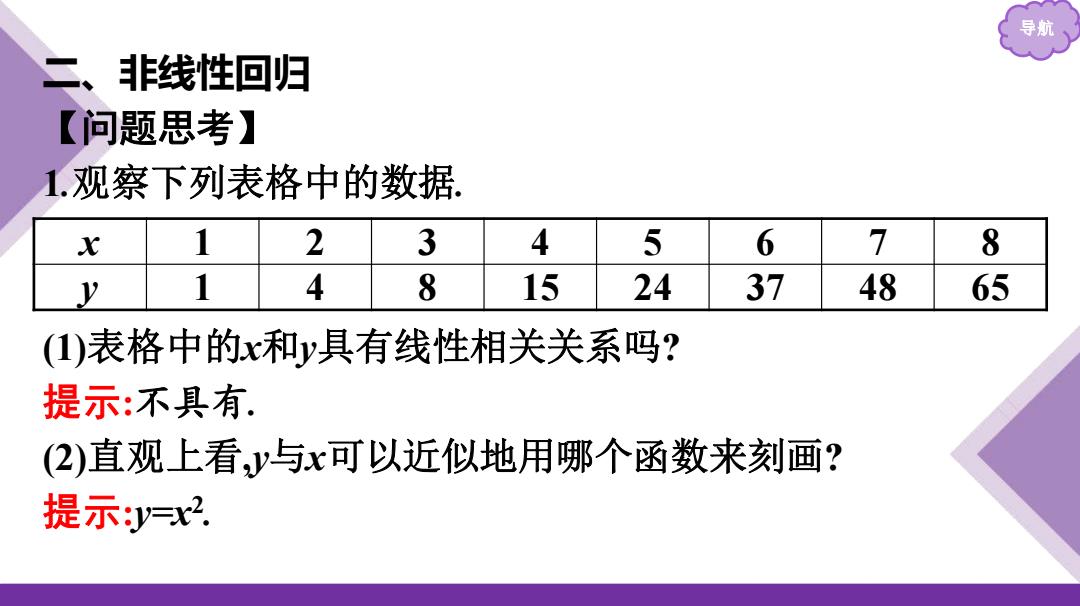
导航 二、非线性回归 【问题思考】 1.观察下列表格中的数据. X 1 2 3 4 5 6 7 8 y 1 4 8 15 24 37 48 65 (1)表格中的x和y具有线性相关关系吗? 提示:不具有. (2)直观上看y与x可以近似地用哪个函数来刻画? 提示:y=x2
导航 二、非线性回归 【问题思考】 1.观察下列表格中的数据. (1)表格中的x和y具有线性相关关系吗? 提示:不具有. (2)直观上看,y与x可以近似地用哪个函数来刻画? 提示:y=x2 . x 1 2 3 4 5 6 7 8 y 1 4 8 15 24 37 48 65

导 2.填空: (1)非线性相关关系与非线性回归方程:当变量y与x的关系不 是 时,称为非线性相关关系,所得到的方程称为 非线性回归方程(也简称为回归方程): (2)非线性回归方程的求解:一般地,非线性回归方程的曲线类 型可以通过作出散点图进行猜测,而回归方程有时可以通过 变量替换后,借助求回归直线的过程确定.当然,确定了非线性 回归方程之后,也可以利用它进行预测:
导航 2.填空: (1)非线性相关关系与非线性回归方程:当变量y与x的关系不 是 线性相关关系时,称为非线性相关关系,所得到的方程称为 非线性回归方程(也简称为回归方程). (2)非线性回归方程的求解:一般地,非线性回归方程的曲线类 型可以通过作出散点图进行猜测,而回归方程有时可以通过 变量替换后,借助求回归直线的过程确定.当然,确定了非线性 回归方程之后,也可以利用它进行预测