
全程设计 第二章 平面解析几何 习题课一圆锥曲线
第二章 平面解析几何 习题课——圆锥曲线
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解圆锥曲线的定义 2.掌握圆锥曲线的标准方程 3.能求解各种圆锥曲线的问题和直线与圆锥曲线的位置关系 问题 4.加强逻辑推理和数学运算能力的培养
导航 课标定位素养阐释 1.了解圆锥曲线的定义. 2.掌握圆锥曲线的标准方程. 3.能求解各种圆锥曲线的问题和直线与圆锥曲线的位置关系 问题. 4.加强逻辑推理和数学运算能力的培养

导航 课前·基础认知 椭圆的定义及标准方程 【问题思考】 1定义:如果F,F2是平面内的两个定点,是一个常数,且 2>FF,则平面内满足PF+PF,=2a的动点P的轨迹称为 椭圆。 2.标准方程: (>b>0), (a>b>0)
导航 课前·基础认知 一、椭圆的定义及标准方程 【问题思考】 1.定义:如果F1 ,F2是平面内的两个定点,a是一个常数,且 2a>|F1F2 |,则平面内满足|PF1 |+|PF2 |=2a的动点P的轨迹称为 椭圆. 2.标准方程: 𝒙 𝟐 𝒂𝟐 + 𝒚 𝟐 𝒃 𝟐 =1 (a>b>0), 𝒚 𝟐 𝒂𝟐 + 𝒙 𝟐 𝒃 𝟐 =1 (a>b>0)

导航 3.离心率ee∈ 4做一微:若椭圆+1的焦距为4则实数m的值 m-2 为 答案:4或8
导航 3.离心率 e= 𝒄 𝒂 ,e∈ (0,1) . 4.做一做:若椭圆 𝒙 𝟐 𝟏𝟎-𝒎 + 𝒚 𝟐 𝒎-𝟐 =1 的焦距为 4,则实数 m 的值 为 . 答案:4或8

导期 二、双曲线的定义及标准方程 【问题思考】 1定义:一般地,如果F,F2是平面内的两个定点,是一个正常 数,且20,b>0), (>0,b>0), 3.离心率e-e∈
导航 二、双曲线的定义及标准方程 【问题思考】 1.定义:一般地,如果F1 ,F2是平面内的两个定点,a是一个正常 数,且2a0,b>0),𝒚 𝟐 𝒂𝟐 − 𝒙 𝟐 𝒃𝟐 =1(a>0,b>0). 3.离心率 e= 𝒄 𝒂 ,e∈(1,+∞)

导航 4双曲线若-二-1a>,b0的渐近线方程为 双曲线器-三1a@b0的渐近线方程为 5做一做:若双曲线号-二-1>0b0)的焦点到其海近线的 距离等于实轴长,则其离心率e= 答案:√5
导航 4.双曲线𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃 𝟐 =1(a>0,b>0)的渐近线方程为 y=± 𝒃 𝒂 x ; 双曲线𝒚 𝟐 𝒂𝟐 − 𝒙 𝟐 𝒃 𝟐 =1(a>0,b>0)的渐近线方程为 y=± 𝒂 𝒃 x . 5.做一做:若双曲线𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃𝟐 =1(a>0,b>0)的焦点到其渐近线的 距离等于实轴长,则其离心率 e= . 答案: 𝟓

导航 三、抛物线的定义及标准方程 【问题思考】 1.定义:一般地,设F是平面内的一个定点,是不过点F的一条 定直线,则平面上到F的距离与到的距离相等的点的轨迹称 为抛物线
导航 三、抛物线的定义及标准方程 【问题思考】 1.定义:一般地,设F是平面内的一个定点,l是不过点F的一条 定直线,则平面上到F的距离与到l的距离相等的点的轨迹称 为抛物线
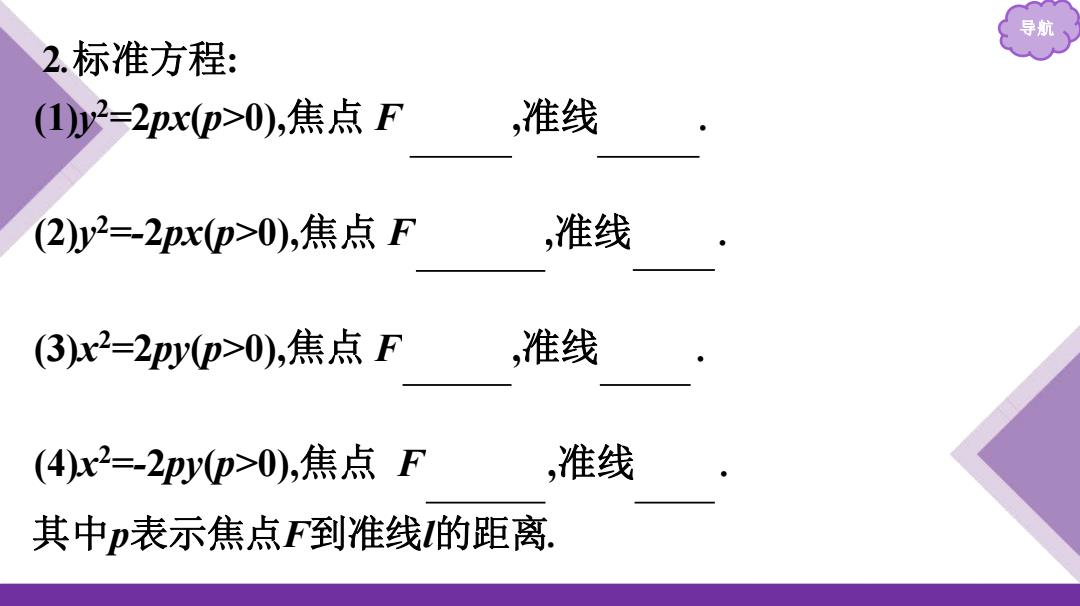
导航 2.标准方程: (1)y2=2px(p>0),焦点F ,准线 (2y2=-2px(D>0),焦点F ,准线 (3)x2=2pyp>0),焦点F ,准线 (4)x2=-2pyp>0),焦点F ,准线 其中p表示焦点F到准线的距离
导航 2.标准方程: (1)y 2 =2px(p>0),焦点 F 𝒑 𝟐 ,𝟎 ,准线 x=- 𝒑 𝟐 . (2)y 2 =-2px(p>0),焦点 F - 𝒑 𝟐 ,𝟎 ,准线 x= 𝒑 𝟐 . (3)x 2 =2py(p>0),焦点 F 𝟎, 𝒑 𝟐 ,准线 y=- 𝒑 𝟐 . (4)x 2 =-2py(p>0),焦点 F 𝟎,- 𝒑 𝟐 ,准线 y= 𝒑 𝟐 . 其中p表示焦点F到准线l的距离

导航 3.做一做:若抛物线y2=-2px的准线经过点(2,2),则该抛物线的 焦点坐标为 答案:(-2,0)
导航 3.做一做:若抛物线y 2=-2px的准线经过点(2,2),则该抛物线的 焦点坐标为 . 答案:(-2,0)