
全程设计 第二章 平面解析几何 2.6 双曲线及其方程 2.6.1 双曲线的标准方程
第二章 平面解析几何 2.6 双曲线及其方程 2.6.1 双曲线的标准方程
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解双曲线的定义、几何图形和标准方程的推导过程 2.会用定义法或待定系数法求双曲线的标准方程, 3.会利用双曲线的定义和标准方程解决简单的问题 4.加强直观想象、逻辑推理和数学运算能力的培养」
导航 课标定位素养阐释 1.了解双曲线的定义、几何图形和标准方程的推导过程. 2.会用定义法或待定系数法求双曲线的标准方程. 3.会利用双曲线的定义和标准方程解决简单的问题. 4.加强直观想象、逻辑推理和数学运算能力的培养

导期 课前·基础认知 双曲线的定义 【问题思考】 1.设F,F,是平面内不重合的两点,则到F和F,的距离之差为0 的点的轨迹是什么? 提示:线段FF的垂直平分线。 2若F,F2是平面内不重合的两点,则到F,和F,的距离之差的 绝对值等于FF的点的轨迹是什么? 提示:直线FF除去F,F2两点之间的部分,即两条射线
导航 课前·基础认知 一、双曲线的定义 【问题思考】 1.设F1 ,F2是平面内不重合的两点,则到F1和F2的距离之差为0 的点的轨迹是什么? 提示:线段F1F2的垂直平分线. 2.若F1 ,F2是平面内不重合的两点,则到F1和F2的距离之差的 绝对值等于|F1F2 |的点的轨迹是什么? 提示:直线F1F2除去F1 ,F2两点之间的部分,即两条射线

导 3.填空:一般地,如果F,F,是平面内的两个定点,是一个正常 数,且2aF1F,则平面上满足 的动点P的轨 迹称为双曲线,其中,两个定点F,F,称为双曲线的焦点,两个焦 点的距离FF,称为双曲线的焦距双曲线可以通过用平面截 两个特殊的圆锥面得到,因此双曲线是一种圆锥曲线
导航 3.填空:一般地,如果F1 ,F2是平面内的两个定点,a是一个正常 数,且2a < |F1F2 |,则平面上满足 ||PF1 |-|PF2 ||=2a 的动点P的轨 迹称为双曲线,其中,两个定点F1 ,F2称为双曲线的焦点,两个焦 点的距离|F1F2 |称为双曲线的焦距.双曲线可以通过用平面截 两个特殊的圆锥面得到,因此双曲线是一种圆锥曲线

导 4.做一做:已知F1(-8,3),F3(2,3),动点P满足PF-PF2=2a,当2a 为8,10时,点P的轨迹分别是( A.双曲线和一条直线 B.双曲线的一支和一条射线 C双曲线的一支和一条直线 D.双曲线和一条射线 答案:B
导航 4.做一做:已知F1 (-8,3),F2 (2,3),动点P满足|PF1 |-|PF2 |=2a,当2a 为8,10时,点P的轨迹分别是( ) A.双曲线和一条直线 B.双曲线的一支和一条射线 C.双曲线的一支和一条直线 D.双曲线和一条射线 答案:B

导航 二、双曲线的标准方程 【问题思考】 1.已知F,F2为定点,如何求出满足PF-PF,=2a(2<FF2) 的动点P的轨迹方程? 提示:坐标法
导航 二、双曲线的标准方程 【问题思考】 1.已知F1 ,F2为定点,如何求出满足||PF1 |-|PF2 ||=2a(2a<|F1F2 |) 的动点P的轨迹方程? 提示:坐标法
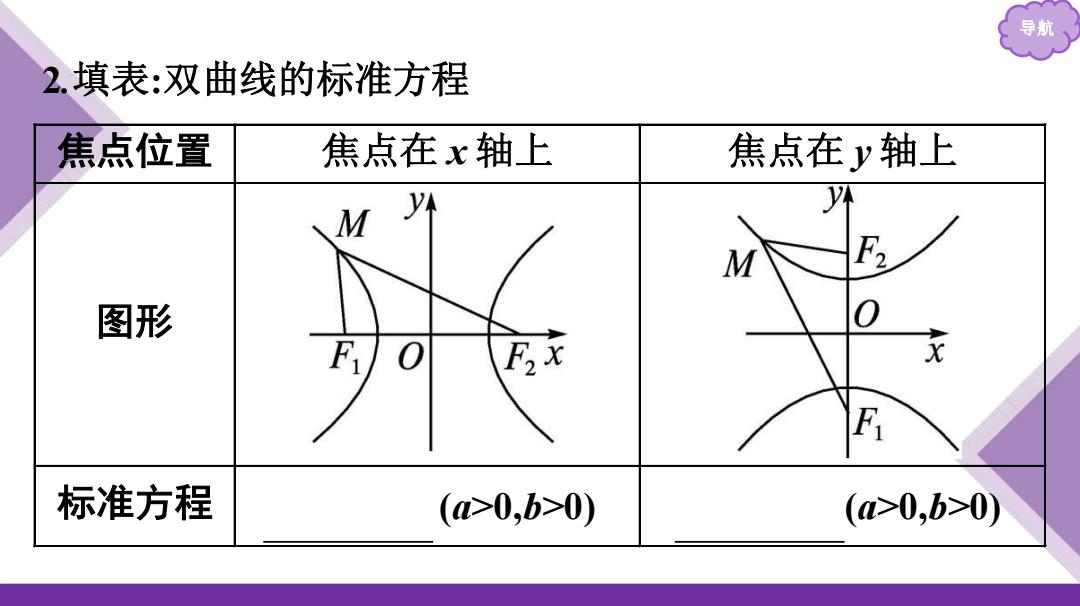
导航 2.填表:双曲线的标准方程 焦点位置 焦点在x轴上 焦点在y轴上 M y M 图形 0 F2x F 标准方程 (a>0,b>0) (a>0,b>0)
导航 2 .填表 :双曲线的标准方 程 焦点位置 焦点在 x 轴上 焦点在 y 轴上 图形 标准方程 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛 𝟐 =1 (a>0,b>0) 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛 𝟐 =1 (a>0,b>0)

导航 焦点位置 焦点在x轴上 焦点在y轴上 焦点坐标 F1(-c,0),Fz(C,0) F0,-C),F20,c) ,b,c的关系
导航 焦点位置 焦点在x轴上 焦点在y轴上 焦点坐标 F1 (-c,0),F2 (c,0) F1 (0,-c),F2 (0,c) a,b,c的关系 c 2=a2+b2

导航 3.做一做:若双曲线的焦距为2,双曲线上一点P到两焦点的距 离之差的绝对值为1,则侧双曲线的标准方程为
导航 3.做一做:若双曲线的焦距为2,双曲线上一点P到两焦点的距 离之差的绝对值为1,则双曲线的标准方程为