
全程设计 第二章 平面解析几何 2.3 圆及其方程 2.3.4 圆与圆的位置关系
第二章 平面解析几何 2.3 圆及其方程 2.3.4 圆与圆的位置关系
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.掌握圆与圆的位置关系及判定方法. 2.能够判定所给两圆的位置关系. 3.能综合应用圆与圆的位置关系解决有关问题 4.加强数学运算和逻辑推理能力的培养」
导航 课标定位素养阐释 1.掌握圆与圆的位置关系及判定方法. 2.能够判定所给两圆的位置关系. 3.能综合应用圆与圆的位置关系解决有关问题. 4.加强数学运算和逻辑推理能力的培养

导航 课前·基础认知 圆与圆的位置关系 【问题思考】 1.两圆的位置关系细分有哪些情况? 提示:外离、外切、相交、内切、内含 2.当两圆的方程联立组成的方程组无解时,两圆一定外离吗? 提示:不一定也可能内含
导航 课前·基础认知 圆与圆的位置关系 【问题思考】 1.两圆的位置关系细分有哪些情况? 提示:外离、外切、相交、内切、内含. 2.当两圆的方程联立组成的方程组无解时,两圆一定外离吗? 提示:不一定.也可能内含
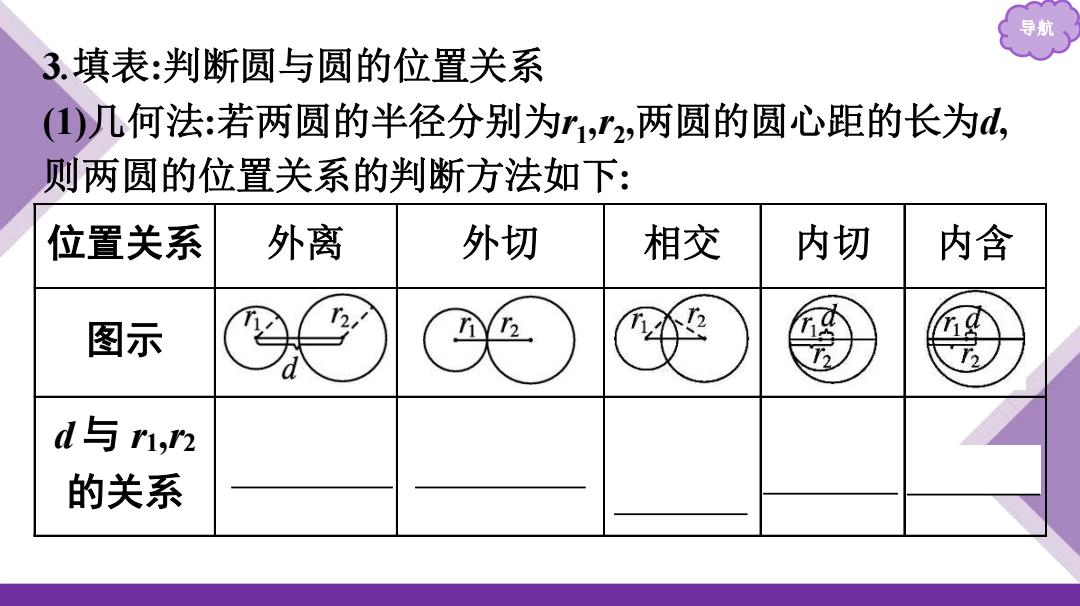
导航 3.填表:判断圆与圆的位置关系 (几何法:若两圆的半径分别为r,2,两圆的圆心距的长为d, 则两圆的位置关系的判断方法如下: 位置关系 外离 外切 相交 内切 内含 图示 个 d与r1,2 的关系
导航 3.填表:判断圆与圆的位置关系 (1)几何法:若两圆的半径分别为r1 ,r2 ,两圆的圆心距的长为d, 则两圆的位置关系的判断方法如下: 位置关系 外离 外切 相交 内切 内含 图示 d 与 r1,r2 的关系 d>r1+r2 d=r1+r2 |r1-r2|< d<r1+r2 d=|r1-r2| d<|r1-r2|

导航 2)代数法:设两圆的一般方程为 C1:x2+y2+Dx+Ey+F=0, C2:x2+y2+D2x+E2y+F2=0, 联立方程得 x2+y2+D1x+E1y+F1=0, x2+y2+D2x+E2y+F2=0, 则方程组解的个数与两圆的位置关系如下: 方程组解的个数 2 1 0 两圆的公共点个数 两圆的位置关系
导航 (2)代数法:设两圆的一般方程为 C1 :x 2+y2+D1x+E1 y+F1 =0, C2 :x 2+y2+D2x+E2 y+F2 =0, 则方程组解的个数与两圆的位置关系如下: 联立方程得 𝒙 𝟐 + 𝒚 𝟐 + 𝑫𝟏 𝒙 + 𝑬𝟏 𝒚 + 𝑭𝟏 = 𝟎, 𝒙 𝟐 + 𝒚 𝟐 + 𝑫𝟐 𝒙 + 𝑬𝟐 𝒚 + 𝑭𝟐 = 𝟎, 方程组解的个数 2 1 0 两圆的公共点个数 2 1 0 两圆的位置关系 相交 外切或内切 外离或内含

导航 4.做一做:两圆x2+y2=9和x2+y2-8x+6y+9=0的位置关系是( A.外离 B.相交 C.内切 D外切 答案:B
导航 4.做一做:两圆x 2+y2=9和x 2+y2 -8x+6y+9=0的位置关系是( ) A.外离 B.相交 C.内切 D.外切 答案:B

导航 【思考辨析】 判断正误(正确的画√”,错误的画“X”) (1)若两圆有一个公共点,则两圆相切.( (2)当两圆的方程组成的方程组无解时,两圆可能内含() (3)当两圆相交时,将两圆的方程相减可得到两圆圆心所在直 线的方程(
导航 【思考辨析】 判断正误.(正确的画“√”,错误的画“×”) (1)若两圆有一个公共点,则两圆相切.( √ ) (2)当两圆的方程组成的方程组无解时,两圆可能内含.( √ ) (3)当两圆相交时,将两圆的方程相减可得到两圆圆心所在直 线的方程.( × )

导航 课堂·重难突破 探究一判断圆与圆的位置关系 【例1】当实数k为何值时,两圆C1x2+y2+4x-6y+12=0,C2: 2+y2-2x-14y+k=0相交、相切、相离? 解:将两圆的一般方程化为标准方程得,C:化+2)2+0y-3)2=1, C2:x-1)2+0y-7)2=50-k 则圆C1的圆心为C(-2,3),半径”=1; 圆C2的圆心为C2(1,7),半径n=V50-k(k<50) 从而CC2(-212+3-7刀2=5
导航 课堂·重难突破 探究一 判断圆与圆的位置关系 【例1】 当实数k为何值时,两圆C1 :x 2+y2+4x-6y+12=0,C2 : x 2+y2 -2x-14y+k=0相交、相切、相离? 解:将两圆的一般方程化为标准方程得,C1 :(x+2)2+(y-3)2=1, C2 :(x-1)2+(y-7)2=50-k. 则圆C1的圆心为C1 (-2,3),半径r1=1; 圆C2的圆心为C2 (1,7),半径 r2=√𝟓𝟎-𝒌(k<50). 从而|C1C2|= (-𝟐-𝟏) 𝟐 + (𝟑-𝟕) 𝟐 =5

导航 当1+V50-k=5,即k=34时,两圆外切; 当√50-k-1=5,即=14时,两圆内切; 当W50-k-15,即k<14时,两圆内含. 故当14<k<34时,两圆相交; 当仁14或=34时,两圆相切; 当k<14或34<k<50时,两圆相离
导航 当 1+√𝟓𝟎-𝒌=5,即 k=34 时,两圆外切; 当|√𝟓𝟎-𝒌-1|=5,即 k=14 时,两圆内切; 当|√𝟓𝟎-𝒌-1|5,即 k<14 时,两圆内含. 故当 14<k<34 时,两圆相交; 当 k=14 或 k=34 时,两圆相切; 当 k<14 或 34<k<50 时,两圆相离