
全程设计 第一章 空间向量与立体几何 习题课 空间向量及其运算
第一章 空间向量与立体几何 习题课——空间向量及其运算
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解空间向量的有关概念、基本定理 2.掌握向量的坐标表示及运算,掌握两向量的数量积 3.能够判断向量的平行和垂直. 4.加强数学运算能力和逻辑推理能力的培养
导航 课标定位素养阐释 1.了解空间向量的有关概念、基本定理. 2.掌握向量的坐标表示及运算,掌握两向量的数量积. 3.能够判断向量的平行和垂直. 4.加强数学运算能力和逻辑推理能力的培养

导航 课前·基础认知 空间向量的有关概念 【问题思考】 1.填表: 名称 定义 记法 零向量 始点和终点 的向量 0 单位向量模等于的向量 lel=1(e为单位向量 相等向量大小“、方向 一的向量 a=b
导航 课前·基础认知 一、空间向量的有关概念 【问题思考】 1.填表: 名称 定义 记法 零向量 始点和终点相同的向量 0 单位向量 模等于1的向量 |e|=1(e为单位向量) 相等向量 大小相等、方向相同的向量 a=b

导航 名称 定义 记法 相反 大小、方向 的向量 a的相反向量为-a 向量 行 向量 两个非零向量方向 或 a ll b 向量 表示向量的有向线段一一在 共面 同一平面内
导航 名称 定义 记法 相反 向量 大小相等、方向相反的向量 a的相反向量为-a 平行 向量 两个非零向量方向相同或相反 a∥b 向量 共面 表示向量的有向线段平移后在 同一平面内 —
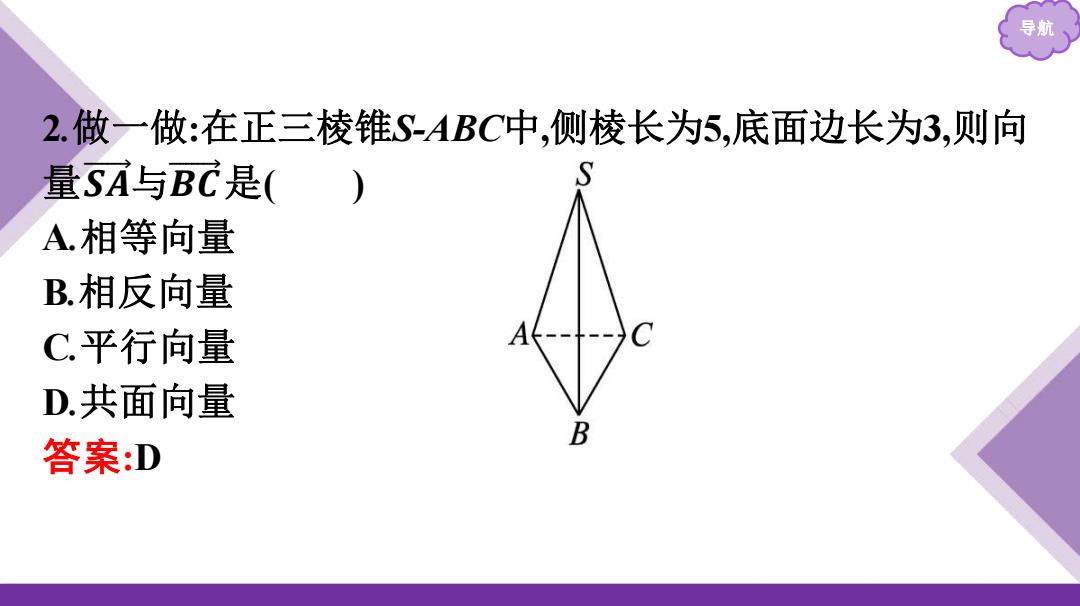
导 2.做一做:在正三棱锥SABC中,侧棱长为5,底面边长为3,则向 量SA与BC是( A.相等向量 B.相反向量 C平行向量 A-- D.共面向量 B 答案:D
导航 2.做一做:在正三棱锥S-ABC中,侧棱长为5,底面边长为3,则向 量 是( ) A.相等向量 B.相反向量 C.平行向量 D.共面向量 答案:D 𝑺 𝑨 与𝑩 𝑪

导航 二、空间向量的有关定理 【问题思考】 1填表: 定理 内容 共线向量 如果a0,且bla,则存在唯一的实数2,使得b=a 基本定理 共面向 若两个向量a,b不共线,则向量a,b,c共面的充要条 量定理 件是,存在唯一的实数对化,y),使c=xyER
导航 二、空间向量的有关定理 【问题思考】 1.填表: 定理 内容 共线向量 基本定理 如果a≠0,且b∥a,则存在唯一的实数λ,使得b=λa 共面向 量定理 若两个向量a,b不共线,则向量a,b,c共面的充要条 件是,存在唯一的实数对(x,y),使c= xa+yb ,x,y∈R

导期 定理 内容 平面向量 若平面内两个向量a与b不共线,则对该平面内任意 基本定理 一个向量c,存在唯一的实数对(c,y),使得c=xa+yb 定理:如果空间中的三个向量a,b,c不共面,那么对 空间中任意一个向量,存在唯一的有序实数组 空间向量 化y,z)使得p= 基本定理 推论:设O,A,B,C是不共面的四点,则对平面ABC内 任一点P都存在唯一的三个有序实数x,y,z,使 OP=xOA+vOB+zOC,x+y=1
导航 定理 内容 平面向量 基本定理 若平面内两个向量a与b不共线,则对该平面内任意 一个向量c,存在唯一的实数对(x,y),使得c=xa+yb 空间向量 基本定理 定理:如果空间中的三个向量a,b,c不共面,那么对 空间中任意一个向量p,存在唯一的有序实数组 (x,y,z)使得p= xa+yb+zc . 推论:设O,A,B,C是不共面的四点,则对平面ABC内 任一点P都存在唯一的三个有序实数x,y,z,使 𝑶 𝑷 =x𝑶 𝑨 +y𝑶 𝑩 +z𝑶 𝑪 ,且 x+y+z=1
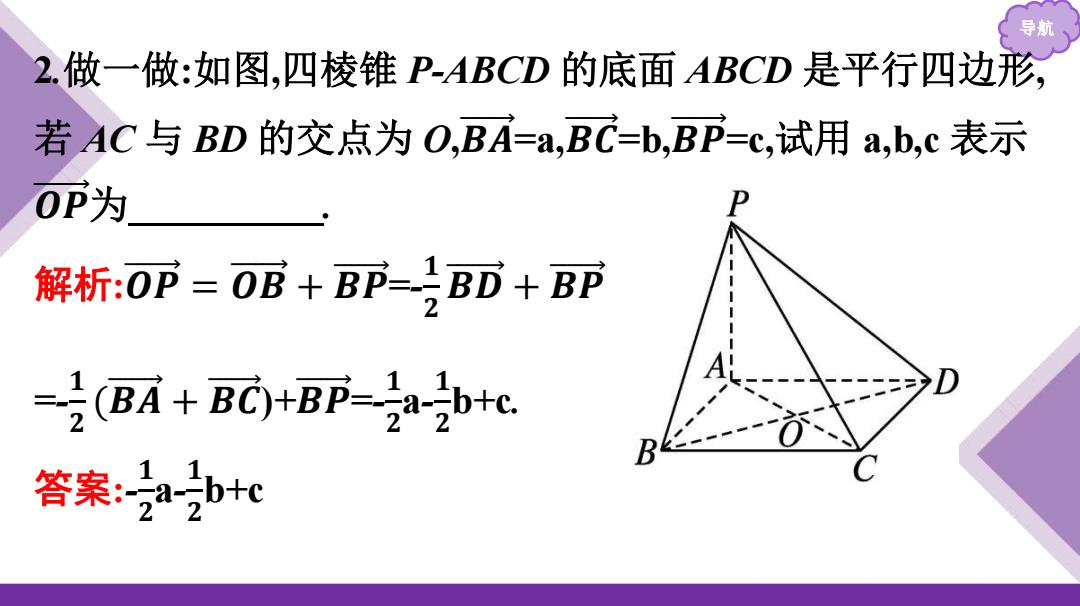
导航 2.做一做:如图,四棱锥P-ABCD的底面ABCD是平行四边形, 若AC与BD的交点为O,BA=a,BC=b,BP=c,试用a,b,c表示 OP为 解析:OP=OB+BP-BD+BP -(BA+BC)+BF-ia-b+c. 答案:2ab+c
导航 2.做一做:如图,四棱锥 P-ABCD 的底面 ABCD 是平行四边形, 若 AC 与 BD 的交点为 O,𝑩 𝑨 =a,𝑩 𝑪 =b,𝑩 𝑷 =c,试用 a,b,c 表示 𝑶 𝑷 为 . 解析:𝑶 𝑷 = 𝑶 𝑩 + 𝑩 𝑷 =- 𝟏 𝟐 𝑩 𝑫 + 𝑩 𝑷 =- 𝟏 𝟐 (𝑩 𝑨 + 𝑩 𝑪 )+𝑩 𝑷 =- 𝟏 𝟐 a- 𝟏 𝟐 b+c. 答案:- 𝟏 𝟐 a- 𝟏 𝟐 b+c

导 三、两个向量的数量积 【问题思考】 1.填空:(1)两个向量的夹角:空间中,给定两个非零向量a,b,任 意在空间中选定一点0,作0A=a,0B=b,则 叫作a与b的 夹角,记作,其范围是 若=2,则 (2)两向量的数量积:ab= 3)空间向量的数量积的性质: ①aLb台 ;②aa==a2;③ab ;④2a)b= ⑤ab=(交换律);⑥(a+b)c=ac+bc(分配律)
导航 三、两个向量的数量积 【问题思考】 1.填空:(1)两个向量的夹角:空间中,给定两个非零向量a,b,任 意在空间中选定一点O,作 ,则∠AOB叫作a与b的 夹角,记作,其范围是[0,π];若= ,则a⊥b . (2)两向量的数量积:a·b=|a||b|cos . (3)空间向量的数量积的性质: ①a⊥b⇔ a·b=0;②a·a= |a| 2 =a 2 ;③|a·b|≤ |a||b|;④(λa)·b=λ(a·b); ⑤a·b=b·a(交换律);⑥(a+b)·c=a·c+b·c(分配律). 𝑶 𝑨 =a,𝑶 𝑩 =b 𝛑 𝟐