
全程设计 复习课 1.空间向量与立体几何
复习课 1.空间向量与立体几何

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破
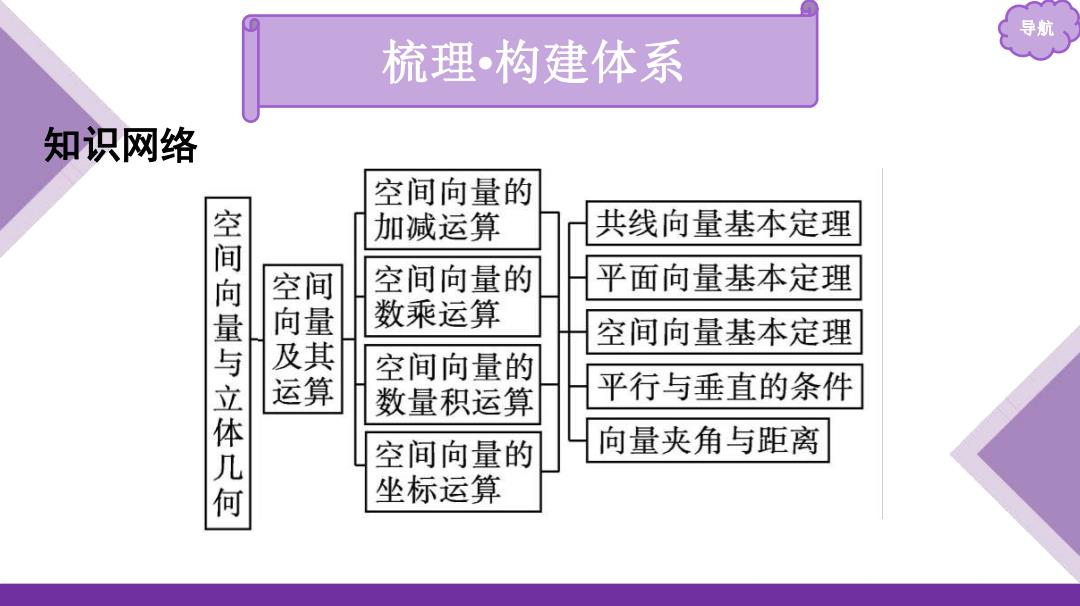
导航 梳理构建体系 知识网络 空间向量的 加减运算 共线向量基本定理 空间向量与立体几何 空 空间向量的 平面向量基本定理 向量 数乘运算 空间向量基本定理 及 空间向量的 运算 数量积运算 平行与垂直的条件 空间向量的 向量夹角与距离 坐标运算
导航 梳理 •构建体系 知识网 络
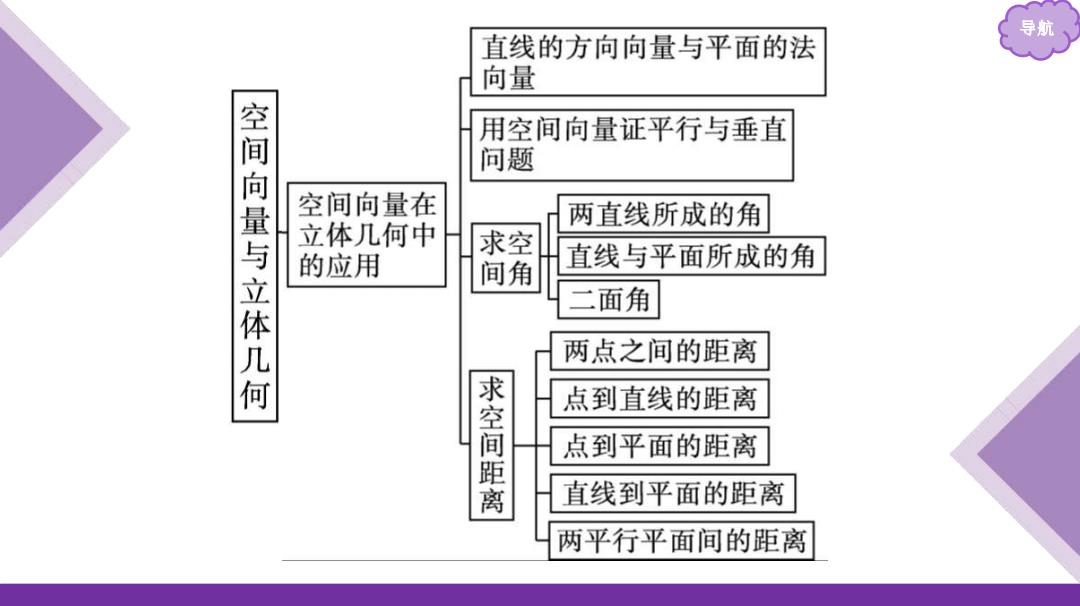
导航 直线的方向向量与平面的法 向量 用空间向量证平行与垂直 空间向量与立体几何 问题 空间向量在 两直线所成的角 立体几何中 求空 的应用 间角 直线与平面所成的角 面角 两点之间的距离 求空间距离 点到直线的距离 点到平面的距离 直线到平面的距离 两平行平面间的距离
导航

导航 要点梳理 1根据空间向量的有关概念,完成下表, 名称 定义 零向量 始点和终点 的向量 共线向量两个非零向量的方向 相等向量 大小一“、方向“一的阿量 表示它们的有向线段✉山“之后,都能在同一平 共面向量 面内
导航 要点梳理 1.根据空间向量的有关概念,完成下表. 名称 定义 零向量 始点和终点相同的向量 共线向量 两个非零向量的方向相同或相反 相等向量 大小相等、方向相同的向量 共面向量 表示它们的有向线段通过平移之后,都能在同一平 面内

导期 2.向量加法运算常应用什么法则?减法运算呢? 提示:平行四边形法则、三角形法则、多边形法则.三角形 法则. 3.数乘向量a(∈R)是如何规定的? 提示:(1)当=0或a=0时,a=0;(2)当≠0,且a≠0时,2a的模为2la, 而且λa的方向:①当>0时,与a的方向相同;②当2<0时,与a的 方向相反
导航 2.向量加法运算常应用什么法则?减法运算呢? 提示:平行四边形法则、三角形法则、多边形法则. 三角形 法则. 3.数乘向量λa(λ∈R)是如何规定的? 提示:(1)当λ=0或a=0时,λa=0;(2)当λ≠0,且a≠0时,λa的模为|λ||a|, 而且λa的方向:①当λ>0时,与a的方向相同;②当λ<0时,与a的 方向相反

导航 4.空间向量的数量积是如何定义的?数量积有哪些性质? 提示:ab=allbcos 性质有:①a⊥b台ab=0;②aa=al2=a2;③abl≤ab④ (2a)b=2(ab)⑤ab=ba(交换律);⑥(a+b)c=ac+bc(分配律)
导航 4.空间向量的数量积是如何定义的?数量积有哪些性质? 提示:a·b=|a||b|cos 性质有:①a⊥b⇔a·b=0;②a·a=|a| 2=a 2 ;③|a·b|≤|a||b|;④ (λa)·b=λ(a·b);⑤a·b=b·a(交换律);⑥(a+b)·c=a·c+b·c(分配律)

导 5.空间向量基本定理有哪些?请填空 (1)共线向量基本定理:如果a≠0,且bla,则存在唯一的实数2,使 得b=a. (2)平面向量基本定理:如果平面内两个向量a与b ,则对 该平面内任意一个向量c,存在唯一的实数对化,y),使得 c-xa+yb
导航 5.空间向量基本定理有哪些?请填空. (1)共线向量基本定理:如果a≠0,且b∥a,则存在唯一的实数λ,使 得b=λa. (2)平面向量基本定理:如果平面内两个向量a与b不共线,则对 该平面内任意一个向量c,存在唯一的实数对(x,y),使得 c=xa+yb

导航 3)共面向量定理:如果两个向量a,b不共线,则向量a,b,c共面的 充要条件是,存在唯一的实数对(化,y),使c=xa+yb. (4)空间向量基本定理:如果空间中的三个向量a,b,c ,那 么对空间中的任意一个向量p,存在唯一的有序实数组(化y,), 使得 其中, 常称为空间向量的一组基底
导航 (3)共面向量定理:如果两个向量a,b不共线,则向量a,b,c共面的 充要条件是,存在唯一的实数对(x,y),使c=xa+yb. (4)空间向量基本定理:如果空间中的三个向量a,b,c不共面,那 么对空间中的任意一个向量p,存在唯一的有序实数组(x,y,z), 使得p=xa+yb+zc.其中,{a,b,c}常称为空间向量的一组基底

导航 6.空间向量的坐标表示,请填空.己知a=(化1y1,1),b=(化2y232),则 (1ua+yb= (u,v∈R). 2)川a=Va'a= 3)ab= (4)alb(a≠0)台. (5)aLb台ab=0台
导航 6.空间向量的坐标表示,请填空.已知a=(x1 ,y1 ,z1 ),b=(x2 ,y2 ,z2 ),则 (1)ua+vb= (ux1+vx2 ,uy1+vy2 ,uz1+vz2 ) (u,v∈R). (3)a·b= x1x2+y1 y2+z1 z2 . (4)a∥b(a≠0)⇔ x2 =λx1 ,y2 =λy1 ,z2 =λz1 . (5)a⊥b⇔a·b=0⇔ x1x2+y1 y2+z1 z2 =0 . (2)|a|= 𝒂·𝒂 = 𝒙𝟏 𝟐 + 𝒚𝟏 𝟐 + 𝒛𝟏 𝟐