
全程设计 第十章 复数 10.1 复数及其几何意义 10.1.2 复数的几何意义
第十章 复数 10.1 复数及其几何意义 10.1.2 复数的几何意义
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.了解复平面的概念 2.理解并掌握复数的几何意义. 3.掌握共轭复数及复数模的定义 4.加强数学抽象、直观想象、数学运算等能力的培养
导航 课标定位素养阐释 1.了解复平面的概念. 2.理解并掌握复数的几何意义. 3.掌握共轭复数及复数模的定义. 4.加强数学抽象、直观想象、数学运算等能力的培养

导航 课前·基础认知 复平面 【问题思考】 1.若复数z确定,则z的实部和虚部是否确定?反之呢? 提示:是反之亦然 2.有序实数对(x,y)与平面直角坐标系中的点是一一对应的吗? 提示:是
导航 课前·基础认知 一、复平面 【问题思考】 1.若复数z确定,则z的实部和虚部是否确定?反之呢? 提示:是.反之亦然. 2.有序实数对(x,y)与平面直角坐标系中的点是一一对应的吗? 提示:是

导期 3.填空:建立了平面直角坐标系来表示复数的平面称为复平 面.在复平面内,x轴上的点对应的都是,因此轴称为实 轴y轴上的点除了外,对应的都是纯虚数,称y轴为虚轴! 4.做一做:若点P在y轴上,则点P对应的复数 是纯虚 数.(填“一定”或“不一定”) 答案:不一定
导航 3.填空:建立了平面直角坐标系来表示复数的平面称为复平 面.在复平面内,x轴上的点对应的都是实数,因此x轴称为实 轴;y轴上的点除了原点外,对应的都是纯虚数,称y轴为虚轴. 4.做一做:若点P在y轴上,则点P对应的复数 是纯虚 数.(填“一定”或“不一定”) 答案:不一定
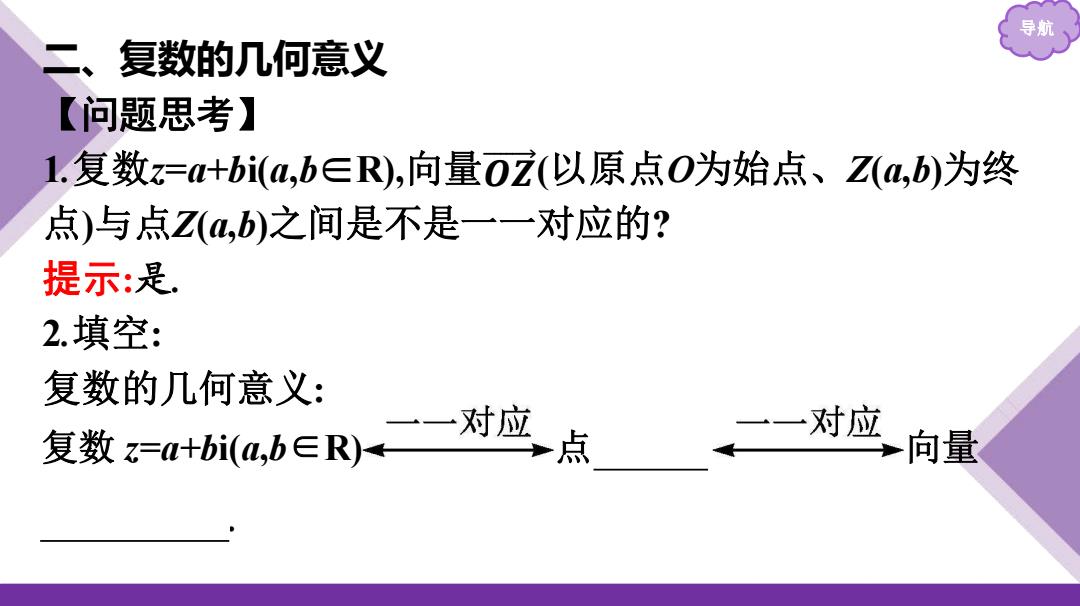
导航 二、复数的几何意义 【问题思考】 1.复数=+bi(a,b∈R),向量0z(以原点O为始点、Z(a,b)为终 点)与点Z(4,b)之间是不是一一对应的? 提示:是 2.填空: 复数的几何意义: 复数:a+hila.6∈RW+一对应点 一一对应 向量
导航 二、复数的几何意义 【问题思考】 1.复数z=a+bi(a,b∈R),向量 (以原点O为始点、Z(a,b)为终 点)与点Z(a,b)之间是不是一一对应的? 提示:是. 2.填空: 复数的几何意义: 𝑶 𝒁 复数 z=a+bi(a,b∈R) 点 Z(a,b) 向量 𝑶 𝒁 = (𝒂, 𝒃)

导航 3.做一做: 在复平面内,0是坐标原点,向量0Z=(-4,-3),0Z对应的复数 7= ;点Z的坐标为 答案:-4-3i(-4,-3)
导航 3.做一做: 答案:-4-3i (-4,-3) 在复平面内,O 是坐标原点,向量𝑶 𝒁 =(-4,-3),𝑶 𝒁 对应的复数 z= ;点 Z 的坐标为

导期 三、共轭复数 【问题思考】 1.在复平面内,已知点A(-6,8)与点A关于实轴对称,试求点A与 点A对应的复数;这两个复数有什么关系? 提示:-6+8i,-6-8i实部相同,虚部互为相反数, 2.填空:一般地,如果两个复数的实部,而虚部互为 则称这两个复数互为共轭复数.复数z的共轭复数用z表示,因 此,当z=a+bi(a,b∈R)时,z=
导航 三、共轭复数 【问题思考】 1.在复平面内,已知点A(-6,8)与点A'关于实轴对称,试求点A与 点A'对应的复数;这两个复数有什么关系? 提示:-6+8i,-6-8i.实部相同,虚部互为相反数. 2.填空:一般地,如果两个复数的实部相等,而虚部互为相反数, 则称这两个复数互为共轭复数.复数z的共轭复数用 表示,因 此,当z=a+bi(a,b∈R)时, = a-bi . 𝒛 𝒛

导航 3.做一做: (1)复数4+i的共轭复数为 (2)复数7的共轭复数为 答案:(1)4-i(2)7
导航 3.做一做: (1)复数4+i的共轭复数为 ; (2)复数7的共轭复数为 . 答案:(1)4-i (2)7

导航 四、复数的模 【问题思考】 1.若复数z=+yixy∈R)对应的向量为0Z,则OZ是多少? 提示:0Z=(xy),0Z=Vx2+y2
导航 四、复数的模 【问题思考】 1.若复数 z=x+yi(x,y∈R)对应的向量为𝑶 𝒁 ,则|𝑶 𝒁 |是多少? 提示:𝑶 𝒁 =(x,y),|𝑶 𝒁 |= 𝒙 𝟐 + 𝒚 𝟐