
全程设计 复习课 2.平面解析几何
复习课 2.平面解析几何

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破
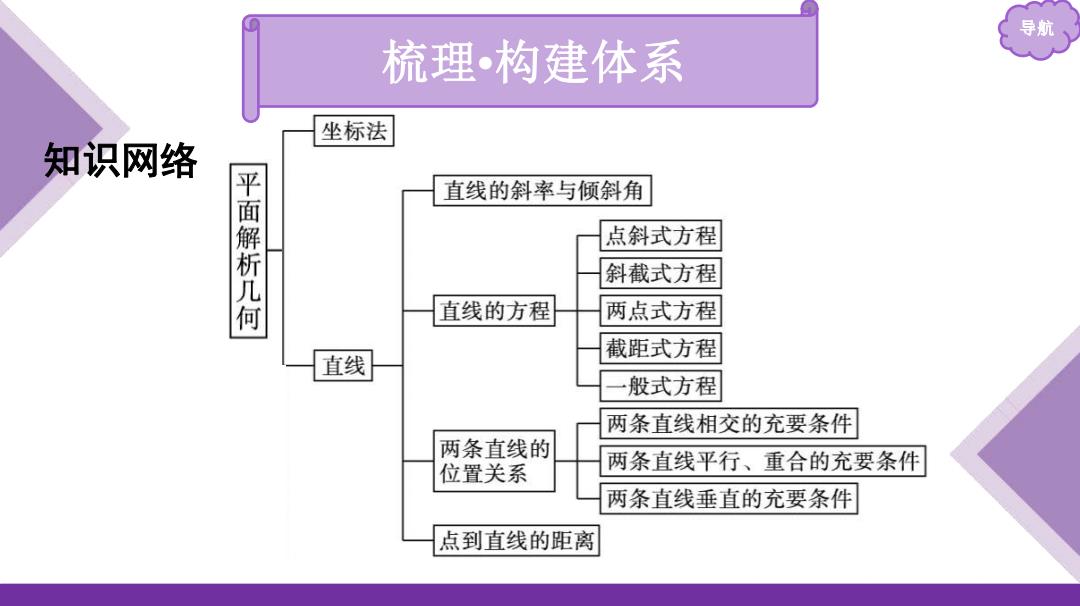
导航 梳理构建体系 坐标法 知识网络 直线的斜率与倾斜角 平面解析几何 点斜式方程 斜截式方程 直线的方程 两点式方程 截距式方程 直线 般式方程 两条直线相交的充要条件 两条直线的 位置关系 两条直线平行、重合的充要条件 两条直线垂直的充要条件 点到直线的距离
导航 梳理 •构建体系 知识网 络
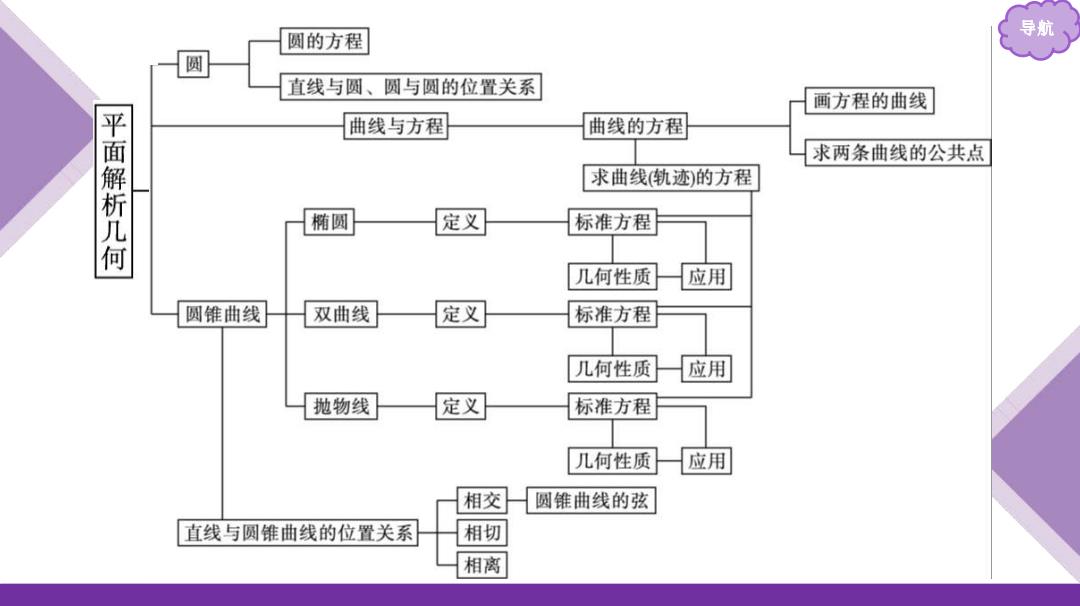
圆的方程 导航 圆 直线与圆、圆与圆的位置关系 画方程的曲线 曲线与方程 曲线的方程 平面解析几何 求两条曲线的公共点 求曲线轨迹)的方程 椭圆 定义 标准方程 几何性质 应用 圆锥曲线 双曲线 定义 标准方程 几何性质 应用 抛物线 定义 标准方程 几何性质 应用 相交 圆锥曲线的弦 直线与圆锥曲线的位置关系 相切 相离
导航

导航 要点梳理 1.点A(c1y1),BK22)之间的距离公式是怎样的? 提示AB=x1-x2)2+y1-y2)2
导航 要点梳理 1.点A(x1 ,y1 ),B(x2 ,y2 )之间的距离公式是怎样的? 提示:|AB|= (𝒙𝟏-𝒙𝟐) 𝟐 + (𝒚𝟏-𝒚𝟐) 𝟐

导航 2.直线的倾斜角是如何定义的?其范围如何? 提示:给定平面直角坐标系中的一条直线,如果这条直线与x 轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重 合时所转的最小正角就是直线的倾斜角 直线与x轴平行或重合时,规定其倾斜角为0°.倾斜角的取值 范围是[0,)
导航 2.直线的倾斜角是如何定义的?其范围如何? 提示:给定平面直角坐标系中的一条直线,如果这条直线与x 轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重 合时所转的最小正角就是直线的倾斜角. 直线与x轴平行或重合时,规定其倾斜角为0° .倾斜角的取值 范围是[0,π)

导 3.直线的斜率公式是什么?直线的倾斜角0与斜率k有何关系? 提示:ky2y,k=tan0. X2-X1 4.试写出倾斜角为0的直线的一个方向向量和一个法向量 提示:方向向量a=(cos0,sin0),法向量b=(sin0,cos0)
导航 3.直线的斜率公式是什么?直线的倾斜角θ与斜率k有何关系? 提示:k=𝒚𝟐-𝒚𝟏 𝒙𝟐-𝒙𝟏 ,k=tan θ. 4.试写出倾斜角为θ的直线l的一个方向向量和一个法向量. 提示:方向向量a=(cos θ,sin θ),法向量b=(-sin θ,cos θ)
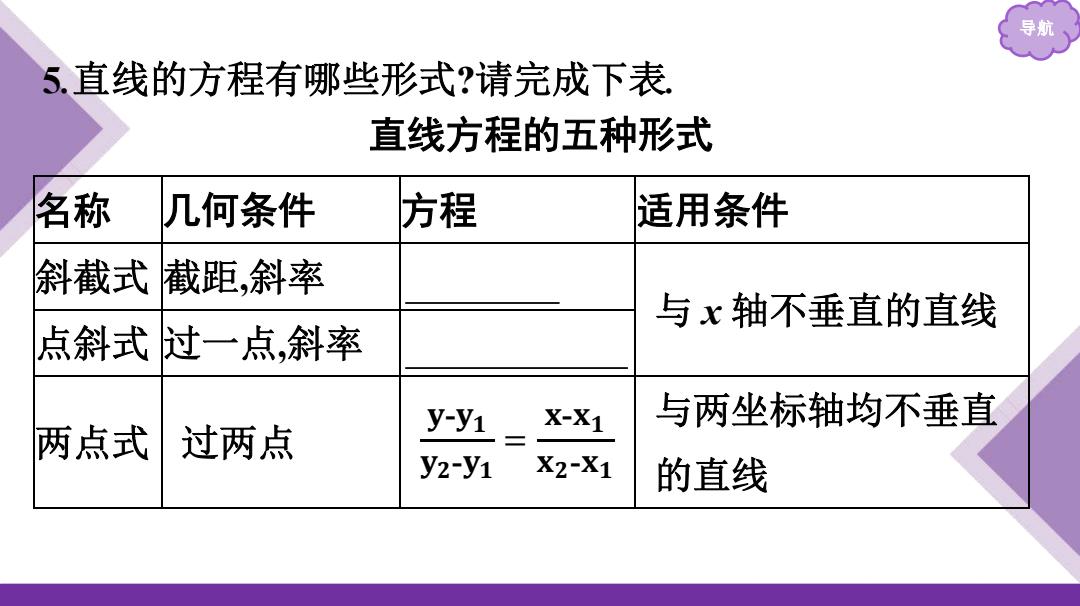
导航 5.直线的方程有哪些形式?请完成下表 直线方程的五种形式 名称 几何条件 方程 适用条件 斜截式 截距,斜率 与x轴不垂直的直线 点斜式过一点,斜率 X-X1 与两坐标轴均不垂直 两点式 过两点 y-y1 y2-y1 X2-X1 的直线
导航 5.直线的方程有哪些形式?请完成下表. 直线方程的五种形式 名称 几何条件 方程 适用条件 斜截式 截距,斜率 y=kx+b 与 x 轴不垂直的直线 点斜式 过一点,斜率 y-y0=k(x-x0) 两点式 过两点 𝐲-𝐲𝟏 𝐲𝟐-𝐲𝟏 = 𝐱-𝐱𝟏 𝐱𝟐-𝐱𝟏 与两坐标轴均不垂直 的直线

导航 名称 几何条件 方程 适用条件 在x轴、y 不过原点,且与两坐标 截距式 轴上的截距 + a 轴均不垂直的直线 Ax+By+C=0 般式 所有直线 (A2+B2+0)
导航 名称 几何条件 方程 适用条件 截距式 在 x 轴、y 轴上的截距 𝐱 𝐚 + 𝐲 𝐛 =1 不过原点,且与两坐标 轴均不垂直的直线 一般式 — Ax+By+C=0 (A2 +B2 ≠0) 所有直线

导 6.怎样判断两条直线平行或垂直? 提示:(1)两条直线平行 对于两条不重合的直线1,2,其斜率分别为k1,k2,则有 L1川2台k1=k2.特别地,当直线l1,2的斜率都不存在时,1与l2平行 (2)两条直线垂直 若两条直线1,2的斜率都存在,设为k1,k2,则11Ll2台k1k2=-1.当 一条直线的斜率为零,另一条直线的斜率不存在时,两条直线 垂直
导航 6.怎样判断两条直线平行或垂直? 提示:(1)两条直线平行 对于两条不重合的直线l1 ,l2 ,其斜率分别为k1 ,k2 ,则有 l1∥l2⇔k1=k2 .特别地,当直线l1 ,l2的斜率都不存在时,l1与l2平行. (2)两条直线垂直 若两条直线l1 ,l2的斜率都存在,设为k1 ,k2 ,则l1⊥l2⇔k1·k2 =-1.当 一条直线的斜率为零,另一条直线的斜率不存在时,两条直线 垂直