
全程设计 第十一章立体几何初步 11.1 空间几何体 11.1.4 棱锥与棱台
第十一章立体几何初步 11.1 空间几何体 11.1.4 棱锥与棱台
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1理解棱锥、棱台的结构特征,并能运用这些特征描述现实生 活中简单物体的结构. 2.掌握棱锥、棱台的定义及形成过程 3.体会数学抽象的过程,加强逻辑推理和数学运算能力的培养
导航 课标定位素养阐释 1.理解棱锥、棱台的结构特征,并能运用这些特征描述现实生 活中简单物体的结构. 2.掌握棱锥、棱台的定义及形成过程. 3.体会数学抽象的过程,加强逻辑推理和数学运算能力的培养

导航 课前·基础认知 一、{ 棱锥 【问题思考】 1.所有面都是三角形的多面体是棱锥吗? 提示:不一定举反例,如两个底面全等的棱锥,使它们的底面 重合后所组成的多面体
导航 课前·基础认知 一、棱锥 【问题思考】 1.所有面都是三角形的多面体是棱锥吗? 提示:不一定.举反例,如两个底面全等的棱锥,使它们的底面 重合后所组成的多面体
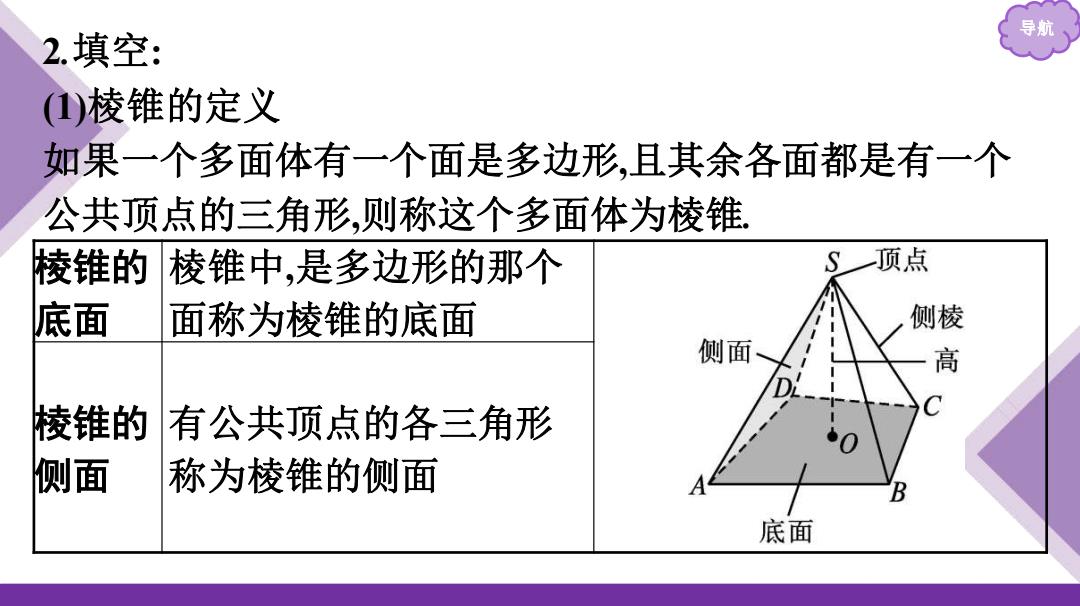
导航 2.填空: (1)棱锥的定义 如果一个多面体有一个面是多边形,且其余各面都是有一个 公共顶点的三角形,则称这个多面体为棱锥 棱锥的 棱锥中,是多边形的那个 S一顶点 底面 面称为棱锥的底面 侧棱 侧面 高 棱锥的 有公共顶点的各三角形 C 侧面 称为棱锥的侧面 底面
导航 2.填空: (1)棱锥的定义 如果一个多面体有一个面是多边形,且其余各面都是有一个 公共顶点的三角形,则称这个多面体为棱锥. 棱锥的 底面 棱锥中,是多边形的那个 面称为棱锥的底面 棱锥的 侧面 有公共顶点的各三角形 称为棱锥的侧面
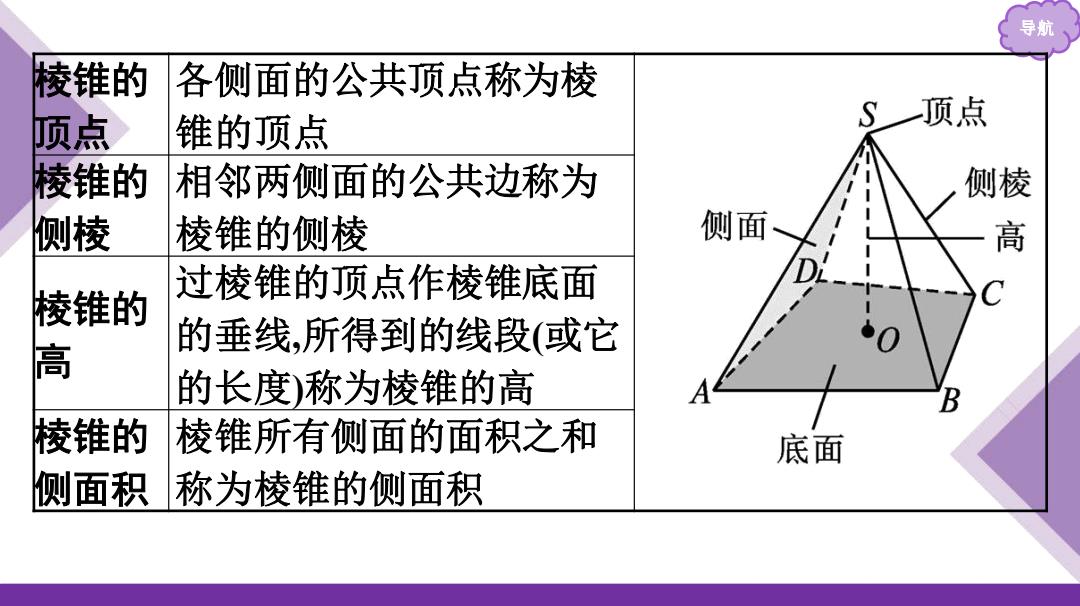
导航 棱锥的 各侧面的公共顶点称为棱 顶点 锥的顶点 S顶点 棱锥的 相邻两侧面的公共边称为 侧棱 侧棱 棱锥的侧棱 侧面 高 过棱锥的顶点作棱锥底面 棱锥的 的垂线,所得到的线段(或它 高 的长度)称为棱锥的高 棱锥的 棱锥所有侧面的面积之和 底面 侧面积 称为棱锥的侧面积
导航 棱锥 的 顶点 各侧面的公共顶点称为棱 锥的顶点 棱锥 的 侧 棱 相邻两侧面的公共边称为 棱锥的侧棱 棱锥的 高 过棱锥的顶点作棱锥底面 的垂线 ,所得到的线段 (或它 的长度 )称为棱锥的高 棱锥 的 侧面积 棱锥所有侧面的面积之和 称为棱锥的侧面积
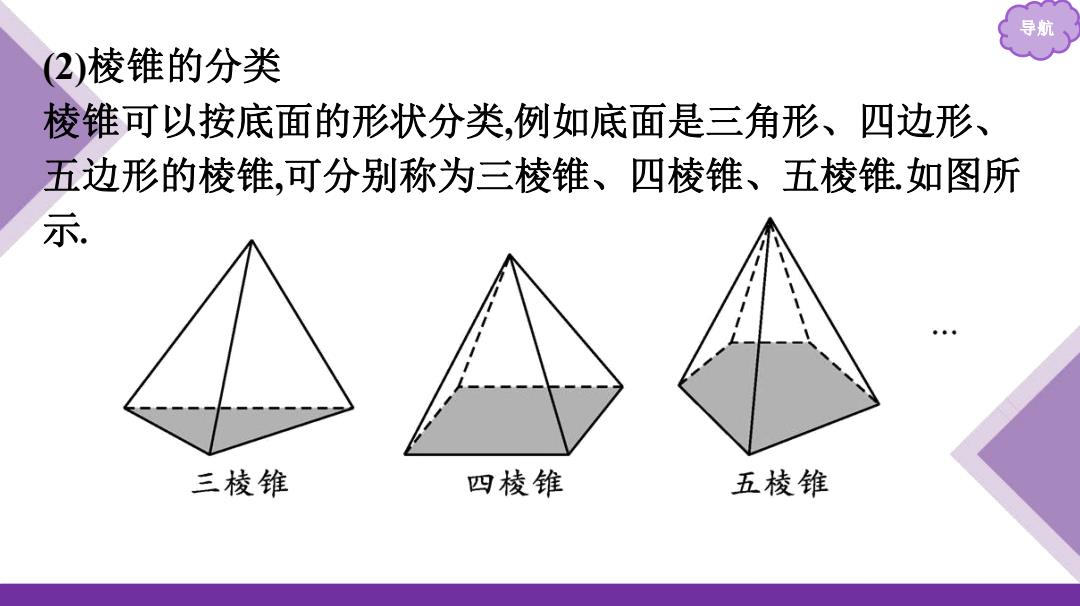
导 2)棱锥的分类 棱锥可以按底面的形状分类,例如底面是三角形、四边形、 五边形的棱锥,可分别称为三棱锥、四棱锥、五棱锥如图所 示 三棱锥 四棱锥 五棱锥
导航 (2)棱锥的分类 棱锥可以按底面的形状分类,例如底面是三角形、四边形、 五边形的棱锥,可分别称为三棱锥、四棱锥、五棱锥.如图所 示

导航 (3)棱锥的表示 棱锥可以用顶点与底面各顶点的字母来表示 (4)正棱锥及相关概念 如果棱锥的底面是 ,且棱锥的顶点与底面 的连 线垂直于底面,则称这个棱锥为正棱锥正棱锥的侧面都全等, 而且都是 三角形,这些等腰三角形底边上的高也都相等, 称为棱锥的
导航 (3)棱锥的表示 棱锥可以用顶点与底面各顶点的字母来表示. (4)正棱锥及相关概念 如果棱锥的底面是正多边形 ,且棱锥的顶点与底面中心的连 线垂直于底面,则称这个棱锥为正棱锥.正棱锥的侧面都全等, 而且都是等腰三角形,这些等腰三角形底边上的高也都相等, 称为棱锥的斜高

导航 3.做一做: 命题:①底面是正多边形的棱锥一定是正棱锥;②所有侧棱长 都相等的棱锥一定是正棱锥;③正棱锥的棱长都相等其中正 确命题的个数为(). A.0B.1C.2D.3
导航 3.做一做: 命题:①底面是正多边形的棱锥一定是正棱锥;②所有侧棱长 都相等的棱锥一定是正棱锥;③正棱锥的棱长都相等.其中正 确命题的个数为( ). A.0 B.1 C.2 D.3

导期 解析:由正棱锥的定义可知①错误; 侧棱长都相等时,底面可以不是正多边形,比如一个三棱锥,侧 棱长都相等,但侧棱的夹角不相等,因此底面边长不相等,不是 正三棱锥,所以②错误; 棱锥的棱包括侧棱和底面的边,正棱锥的侧棱长都相等,底面 边长都相等,但侧棱长和底面边长可能不相等,所以③错误 综上,选A 答案:A
导航 解析:由正棱锥的定义可知①错误; 侧棱长都相等时,底面可以不是正多边形,比如一个三棱锥,侧 棱长都相等,但侧棱的夹角不相等,因此底面边长不相等,不是 正三棱锥,所以②错误; 棱锥的棱包括侧棱和底面的边,正棱锥的侧棱长都相等,底面 边长都相等,但侧棱长和底面边长可能不相等,所以③错误. 综上,选A. 答案:A