
全程设计 第四章 指数函数、对数函数与幂函数 4.4幂函数
第四章 指数函数、对数函数与幂函数 4.4 幂函数

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 幂函数的概念 【问题思考】 1.函数yx,y1x1有哪些共同的结构特点? 提示:解析式是一个幂,幂底数只有一个自变量X,幂指数是常 数. 2.填空:一般地,函数 称为幂函数,其中为常数,是自 变量
导航 课前·基础认知 一、幂函数的概念 【问题思考】 1.函数 y=x,y=x2 ,y= 𝟏 𝒙 =x-1 有哪些共同的结构特点? 提示:解析式是一个幂,幂底数只有一个自变量x,幂指数是常 数. 2.填空:一般地,函数y=xα 称为幂函数,其中 α 为常数, x 是自 变量

导航 二、 幂函数的性质 【问题思考】 1.若让你作出函数y=x3,y=x2的图象,你会按怎样的步骤进行? 提示:先求定义域,再研究函数性质(奇偶性、单调性、对称性 等),然后用描点法作出图象(或部分图象),最后成图
导航 二、幂函数的性质 【问题思考】 1.若让你作出函数y=x3 ,y= 的图象,你会按怎样的步骤进行? 提示:先求定义域,再研究函数性质(奇偶性、单调性、对称性 等),然后用描点法作出图象(或部分图象),最后成图. 𝒙 𝟏 𝟐
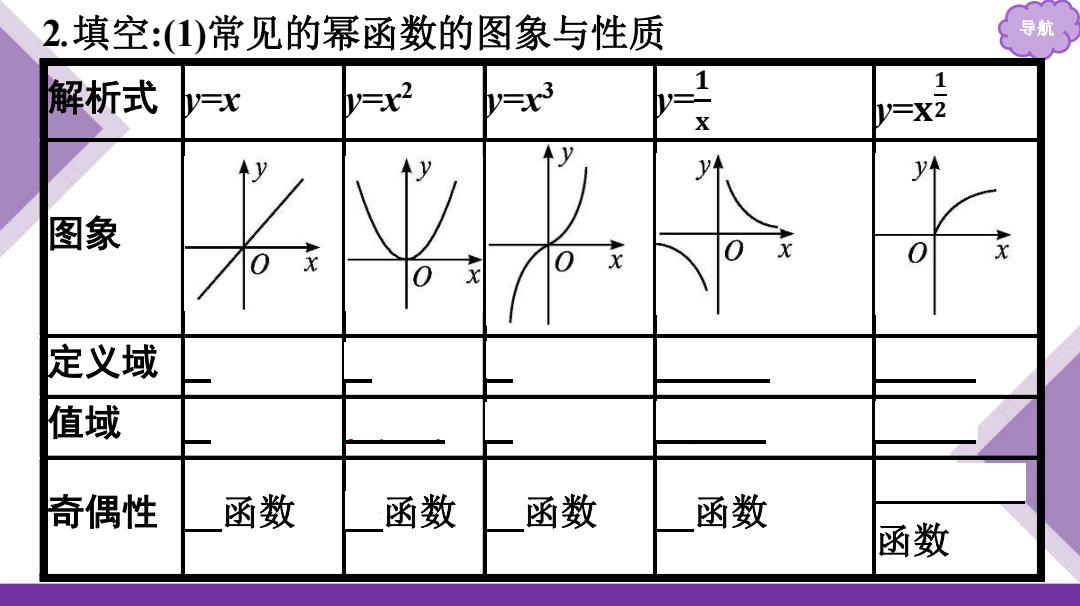
2.填空:(1)常见的幂函数的图象与性质 导航 解析式 y=x =x2 y=x3 1 1 X V-X2 ↑y y y 图象 0 x 0 0 定义域 值域 奇偶性 函数 函数 函数 函数 函数
导航 2 .填空:(1)常见的幂函数 的图象与性质 解析式 y=x y=x 2 y=x 3 y= 𝟏𝐱 y= 𝐱 𝟏𝟐 图象 定义域 R R R {x|x≠0} [0, + ∞) 值域 R [0, + ∞) R {y|y ≠0} [0, + ∞) 奇偶性 奇函数 偶函数 奇函数 奇函数 非奇非偶 函数
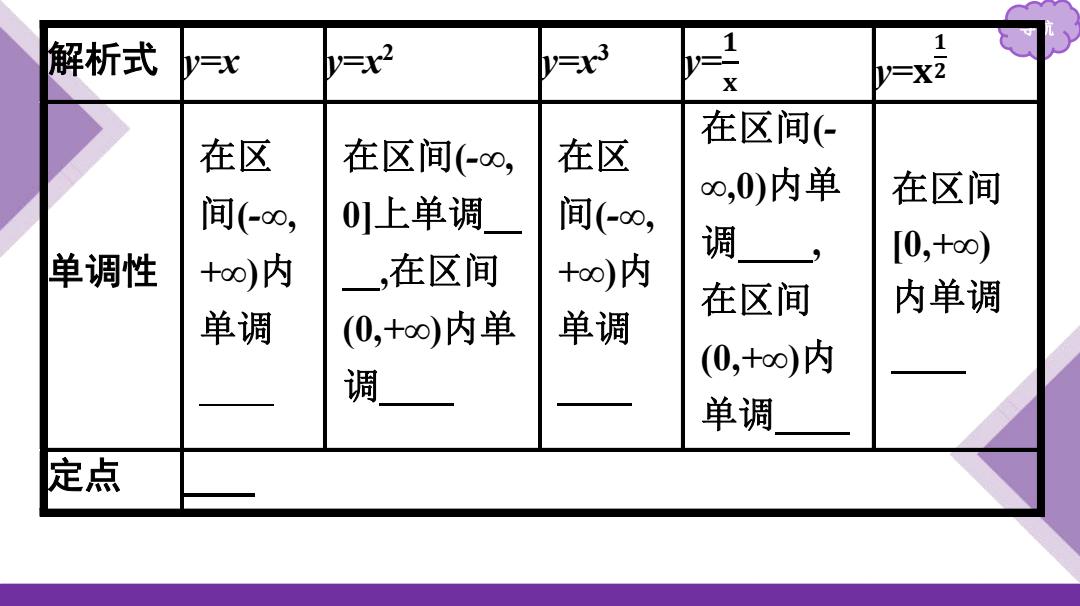
解析式 1 y=x y=x2 =x3 X =X2 在区间( 在区 在区间(-0, 在区 00,0)内单 在区间 间(-o0, 0]上单调 间(-o0, 调 [0,+oo) 单调性 +oo)内 ,在区间 +o)内 在区间 内单调 单调 (0,+o∞)内单 单调 (0,+o)内 调 单调 定点
导航 解析式 y=x y=x2 y=x3 y= 𝟏 𝐱 y=𝐱 𝟏 𝟐 单调性 在区 间(-∞, +∞)内 单调 递增 在区间(-∞, 0]上单调递 减,在区间 (0,+∞)内单 调递增 在区 间(-∞, +∞)内 单调 递增 在区间(- ∞,0)内单 调递减, 在区间 (0,+∞)内 单调递减 在区间 [0,+∞) 内单调 递增 定点 (1,1)

(2)幂函数y=x的性质 ①所有的幂函数在区间(0,+∞)内都有定义,因此在第一象限内 都有图象,并且图象都通过点 ②如果>0,则幂函数的图象通过 ,且在区间[0,+oo)内是 函数. ③如果a<0,则幂函数在区间(0,+∞)内是减函数,且在第一象限 内:当x从右边趋向于原点时,图象在y轴右方且无限地逼近y轴; 当x无限增大时,图象在x轴上方且无限地逼近x轴
导航 (2)幂函数y=xα的性质 ①所有的幂函数在区间(0,+∞)内都有定义,因此在第一象限内 都有图象,并且图象都通过点(1,1). ②如果α>0,则幂函数的图象通过原点,且在区间[0,+∞)内是增 函数. ③如果α<0,则幂函数在区间(0,+∞)内是减函数,且在第一象限 内:当x从右边趋向于原点时,图象在y轴右方且无限地逼近y轴; 当x无限增大时,图象在x轴上方且无限地逼近x轴

导航 3.做一做:下列说法中,正确的是( A幂函数y=xy=x的图象都过点(0,0),(1,1) B.当a=1,2,3,2,1时,幂函数y=x的图象都经过第一、三象限 C在幂指数a取1,3,时,幂函数y=x是增函数 D.当幂指数=-1时,幂函数y=x在其整个定义域上是减函数 答案:C
导航 3.做一做:下列说法中,正确的是( ) A.幂函数y=x-1 ,y=x的图象都过点(0,0),(1,1) B.当α=1,2,3, ,-1时,幂函数y=xα的图象都经过第一、三象限 C.在幂指数α取1,3, 时,幂函数y=xα是增函数 D.当幂指数α=-1时,幂函数y=xα在其整个定义域上是减函数 答案:C 𝟏 𝟐 𝟏 𝟐
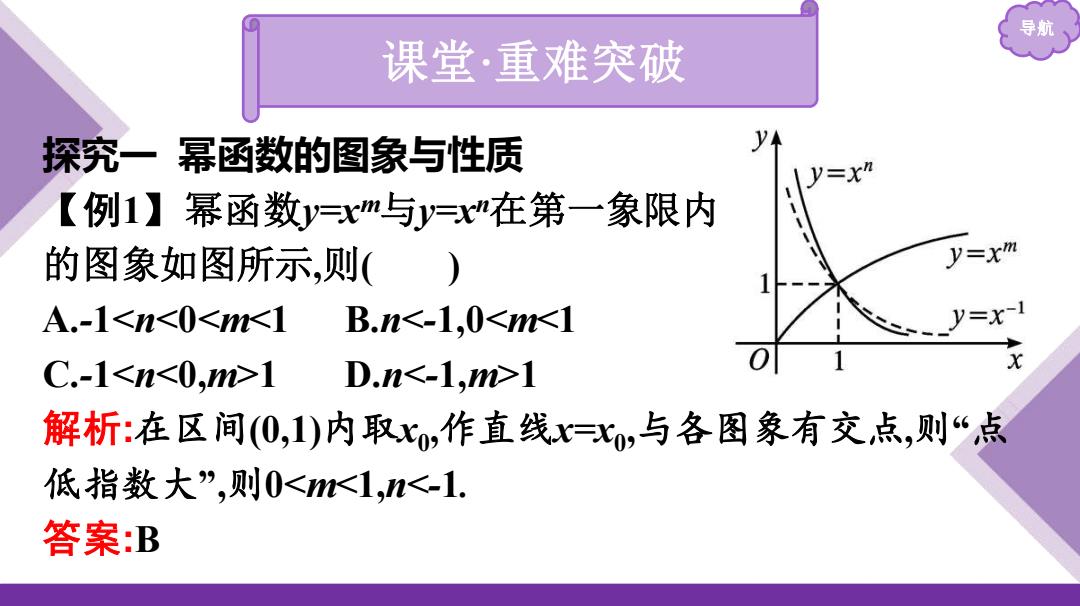
导航 课堂·重难突破 探究一幂函数的图象与性质 y y=xm 【例1】幂函数y=xm与y=x"在第一象限内 的图象如图所示,则() y=xm A.-11 D.n1 解析:在区间(0,1)内取x,作直线x=xo,与各图象有交点,则“点 低指数大”,则0<1,n<-1. 答案:B
导航 课堂·重难突破 探究一 幂函数的图象与性质 【例1】幂函数y=x m与y=x n在第一象限内 的图象如图所示,则( ) A.-11 D.n1 解析:在区间(0,1)内取x0 ,作直线x=x0 ,与各图象有交点,则“点 低指数大”,则0<m<1,n<-1. 答案:B

导航 反思感悟依据图象高低判断幂指数大小,相关结论为:在区间 0,1)内,指数越大,幂函数图象越靠近x轴;在区间(1,+oo)内,指 数越大,图象越远离x轴
导航 反思感悟 依据图象高低判断幂指数大小,相关结论为:在区间 (0,1)内,指数越大,幂函数图象越靠近x轴;在区间(1,+∞)内,指 数越大,图象越远离x轴